Методы решения задач механики грунтов

Механика грунтов является прикладной дисциплиной, призванной изучать и количественно описывать механические процессы, протекающие в грунтах в результате строительства.

Состав задач, которые приходится при этом решать, очень широк и многообразен. Реакция различных видов грунтов на воздействия при строительстве также очень разнообразна. Тем не менее, механика грунтов как научная дисциплина содержит единый методологический подход к решению всех этих задач независимо от вида и состояния грунтов.

Общим методом механики грунтов, как и вообще механики сплошной деформируемой среды, является решение краевых задач, т. е. совместное решение уравнений равновесия, геометрических соотношений или получаемых из них уравнений неразрывности и физических уравнений при заданных краевых (начальных и граничных) условиях.

Это позволяет определить напряженно-деформированное состояние в любой точке массива грунта и в конечном счете оценить прочность грунта в этой точке, устойчивость массива и взаимодействующего с ним сооружения и принять оптимальное решение о строительстве сооружения.

Уравнения равновесия и геометрические соотношения справедливы при любом законе деформирования грунта. Поскольку именно физические уравнения устанавливают связь между напряжениями и деформациями, т: е. определяют особенности напряженно-деформированного состояния грунта, их часто называют определяющими уравнениями или уравнениями состояния.

В зависимости от сложности задачи (класса ответственности сооружения, особенностей деформирования грунтов и т. п.) решение механики грунтов могут быть и очень сложными, и относительна простыми. Например, при проектировании оснований и фундаментов реакторного отделения АЭС или платформы для добычи нефти на шельфе из-за очень больших размеров сооружений, сложных нагрузок и воздействий, жестких технологических требований к эксплуатации этих сооружений, опасности аварийных последствий потребуются более сложные решения, чем при проектирован оснований и фундаментов типового здания. Соответственно и уравнения состояния для этих задач должны будут в разной мере учитывать всю полноту процессов, происходящих в грунтах основания.

Правильный выбор вида уравнений состояния для конкретных условий является одной из основных задач механики грунтов. С этой целью проводятся эксперименты, выявляющие особенности деформирования грунтов под нагрузкой, и с использованием то или иной расчетной модели грунта дается математическое описание результатов этих экспериментов. Таким образом, уравнения состояния имеют феноменологический характер.

Мерой количественной оценки напряженно-деформированного состояния массива грунтов являются напряжения, деформации и перемещения, возникающие в нем от действия внешних (нагрузки от сооружения) и внутренних (массовых) сил.

С учетом изложенного выше, понятия о напряжениях, деформациях и перемещениях в грунтах соответствуют общим понятиям механики сплошной среды.

Тогда напряженно-деформированное состояние в точке массива вполне определено, если известны:

1) три компоненты нормальных (σ_х, σ_у σ_z и три пары касательных (τ_ху = τ_ух, τ_xz = τ_zх, τ_yz = τ_zy) напряжений;

2) три компоненты линейных (ε_х, ε_у, ε_z) и три пары угловых (γ_ху = γ_ух, γ_хz = γ_zх, γ_уz = γ_zу) деформаций;

3) три компоненты перемещений (u, v, w).

Поскольку грунты, как правило, очень плохо работают на растяжение, в механике грунтов в отличие от механики сплошной среды сжимающие напряжения принимаются со знаком плюс, а растягивающие — со знаком минус.

При определении напряженно-деформированного состояния грунта часто пользуются понятиями главных напряжений и главных деформаций, не зависящих (инвариантных) от выбора положения осей координат х, у, z. Напомним, что главными нормальными напряжениями называются нормальные напряжения, отнесенные к главным площадкам, на которых касательные напряжения равны нулю. При этом всегда принимается, что σ₁ ≥ σ₂ ≥ σ₃. Зная главные нормальные напряжения, можно определить и главные касательные напряжения, действующие на площадках, где они достигают наибольших значений:

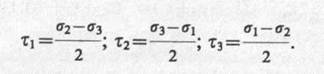(3.1)

Аналогичным образом можно определить и главные деформации. Связь между главными напряжениями, главными деформациями и соответствующими компонентами напряжений и деформаций по осям х, у, z, а также положения главных площадок определяются общим правилам механики сплошной среды. Иногда бывает удобно общее напряженное деформированное состояние в точке массива грунта разделить две составляющие. Применительно к напряженному состоянию показано на рис. 4.1. Тогда общее напряженное состояние (тензор напряжений), определяемое 9-тью компонентами напряжений (рис.4.1,а), выразится как сумма гидростатического напряженного состояния (шаровой тензор), вызывающего изменение только объема грунта (рис. 4.1, б), и девиаторного напряженного состояния (девиатор напряжений), вызывающего изменение только его формы (рис. 4.1, в). Аналогично можно разделить и общее деформированное состояние в точке массива грунта.

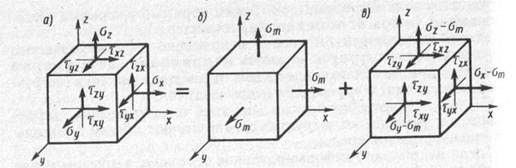
Рис. 4.1. Разложение тензора напряжений (а) на шаровой тензор (б) и девиатор напряжений (в)

Это позволяет использовать в описании поведения грунта приводимые ниже инвариантные (не зависящие от положения осей координат) характеристики его напряженно-деформированного состояния:

- среднее нормальное (гидростатическое) напряжение σ_m, вызывающее изменение объема вырезанного из грунта элементарного параллелепипеда, соответствующую ему среднюю линейную деформацию ε_m и общую объемную деформацию ε_V, равные

- интенсивность касательных напряжений τ_i – комбинацию напряжений. Следствием действия которых является изменение формы элементарного параллелепипеда, характеризуемое интенсивностью деформаций сдвига γ_i, где

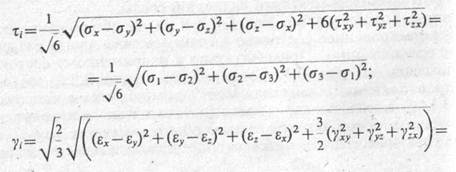
Приведенные выше инварианты напряжений и деформаций используются при описании результатов экспериментов для составления уравнений состояния ряда расчетных моделей грунта.

Дата добавления: 2014-01-05