
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекций по микроэкономике 17 страница
|
|
|
|
Всегда ли, однако, точка потребительского оптимума характеризуется выражением (8)?
Для ответа на этот вопрос нам придется рассмотреть различные типы карт безразличия.
1. Кривые безразличия не достигают осей координат, а асимптотически приближаются к ним или к иным прямым, параллельным осям координат (рис. 6). Это означает, что сколь бы ни был велик объем потребления одного из товаров, он все же не может компенсировать полное отсутствие другого товара в наборе (иначе говоря, ни один из товаров не может быть полностью заменен другим, т. е. потребитель не может обойтись без какого-то количества каждого из товаров).
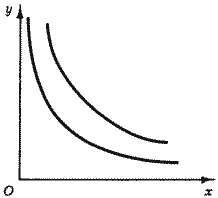
Рис. 6. Кривые безразличия не касаются осей координат
В этом случае при движении вдоль кривой безразличия норма замещения изменяется от нуля до бесконечности, и каково бы ни было соотношение цен PX/PY, точка равновесия будет отвечать условию (8).
2. Кривые безразличия имеют общие точки с одной или обеими осями координат (рис. 7), т. е. потребитель может полностью отказаться от некоторого товара, компенсируя этот отказ увеличенным потреблением другого. При этом может оказаться, что на всей кривой безразличия MRS > PX/PY или MRS < PX/PY.

Рис. 7. Кривые безразличия имеют общие точки с осями координат
Где же будет в этих случаях располагаться точка потребительского оптимума? Рассмотрим рис. 8,а.

Рис. 8. Угловые положения потребительского оптимума
Очевидно, что потребитель достигает наивысшей из доступных кривых безразличия в точке А, где MRS < PX/PY, и расходует все свои денежные средства исключительно на приобретение товара Y (х = 0). Товар Х оказывается слишком дорогим для данного потребителя. На рис. 8,б показан случай, когда потребитель расходует все денежные средства на товар X, и в точке потребительского оптимума MRS > PX/PY.
Точки А (рис. 8,а) и В (рис. 8,б) носят название углового решения задачи потребительского выбора в противоположность внутреннему решению (точка Е на рис. 5).
Отметим, что если для двухтоварного случая угловое решение является некой особой ситуацией, то для случая достаточно большого числа товаров угловое решение представляет собой скорее правило, чем исключение: ведь никто в самом деле не приобретает все те товары, которые предлагает ему рынок. Все же, оставаясь в рамках двухтоварной модели, мы будем в дальнейшем рассматривать главным образом внутреннее решение, считая выражение (8) условием оптимума потребителя.
В лекции 15 мы перейдем к решению следующей задачи, стоящей перед теорией поведения потребителя, — изучить, как изменяется оптимум потребителя при изменении границ множества доступных данному потребителю наборов товаров, т. е. при изменении дохода и цен.
РАЗДЕЛ 3. От порядковой полезности к количественной
Что нужно для количественного измерения
После классических работ Дж. Хикса и Р. Аллена ординалистский подход к полезности завоевал признание экономистов-теоретиков; они утвердились в мнении о том, что поведение потребителя можно достаточно полно описать на основе допущения о наличии у него предпочтений одних наборов благ перед другими.
Какие факты могли бы свидетельствовать о существовании количественной полезности?
Таким фактом, если бы его удалось обнаружить, было бы умение потребителя сопоставлять не только наборы благ, но и различия между парами наборов. Скажем, А > В и С > D. Если потребитель сможет определить, какое из преимуществ — А перед B или С перед D — значительнее, либо же сможет сказать, что оба преимущества равноценны, то эта способность, проявляясь в актах потребительского выбора, могла бы служить основой для построения количественной шкалы измерений.
Действительно, допустим, что А > В и что нам удалось найти такой набор С (А > С > В), что преимущество А перед С равнозначно преимуществу С перед В. Это позволяет утверждать, что полезность набора С расположена “точно в середине” между полезностями A и B, И если мы придали какие-то количественные значения полезности U(А) и U(B), то мы должны полезности набора С приписать значение:
| U(C) = (U(A) + U(B))/2. |
Затем мы можем разделить интервал полезностей между А и С еще раз пополам и продолжить этот процесс сколь угодно далеко, построив шкалу полезностей с любой нужной точностью.
Но мы могли бы построить шкалу не только для полезностей, промежуточных между A и B. Допустим, мы нашли набор D(А > В > D), такой, что превосходство А перед В равнозначно превосходству В перед D. Теперь уже полезность В располагается посредине между А и D, и поэтому:
| U(B) = (U(A) + U(D))/2, |
так что:
| U(D) = 2U(B) – U(A). |
Таким образом, умея сравнивать пары наборов по степени предпочтительности и задав численные значения полезностям двух наборов, мы однозначно определили бы численные значения полезностей любых наборов.
Подобные ситуации возникали и в естественных науках. Примером может служить установление количественной шкалы температур. Человек по своим ощущениям может установить отношения “теплее”, “холоднее” — это не количественное, а лишь порядковое отношение. При контакте двух по-разному нагретых тел одно из них нагревается, другое — охлаждается до выравнивания температуры. “Тепло” (смысл этого понятия до поры до времени был неясен, поэтому мы и берем это слово в кавычки) всегда перетекает от более нагретого тела к более холодному. Но и эти факты не выводят за пределы порядковой шкалы температур.
Положение изменилось, когда появилась концепция, связывающая передачу “тепла” с изменением температуры. Для построения количественной шкалы оказалось достаточно двух принципов: 1) при контакте двух тел общее количество “тепла” в них не изменяется; 2) равные количества “тепла”, переданные одинаковым телам, вызывают одинаковые изменения температуры.
Если мы, смешав воду из сосудовА и В в равных количествах, получили воду точно такой же температуры, что и в сосуде С, у нас есть основания считать, что разность температур между А и С такая же, как между С и В. Если в сосуде А только что растаял лед и мы приняли его температуру за 0, а в сосуде В вода кипела, и мы приняли ее температуру за 100, то мы должны придать значение 50 для температуры воды в сосуде С. Теперь мы можем отградуировать термометр. Значения 0 и 100 мы приняли произвольно. Поступив таким образом, мы построили температурную шкалу Цельсия. Задавая другие значения, мы изменили бы начало отсчета и единицу температуры; при соответствующем выборе мы могли бы получить температурные шкалы Реомюра или Фаренгейта. Переход от одной из них к другой выражается соотношением:
| t1 = a + bt2. |
Свободный член а характеризует перенос начала отсчета, а коэффициент b — соотношение единиц.
Вильфредо Парето, анализируя сложившуюся к последнему десятилетию XIX в. количественную теорию полезности, увидел в ней слабое звено. Поскольку, по мнению Парето, поведение потребителя не обнаруживает его способности сопоставлять одну пару наборов с другой, гипотеза о существовании количественной меры полезности не вытекала из наблюдаемых фактов и ее отрицание не входило в противоречие с опытом.
Значит, она “лишняя”, и нужно строить теорию предпочтения, обходясь без нее. аков был методологический принцип, уже на протяжении веков утвердившийся в науке и получивший название “бритва Оккама”.
Позднее Дж. Хикс и Р. Аллен построили развитую теорию потребления, базирующуюся лишь на порядковых шкалах индивидуальных предпочтений.
Между тем факты потребительского поведения, для описания которых порядковое представление о полезности недостаточно, существовали. Но они относились к таким аспектам потребительского выбора, которые в то время не привлекали внимания экономистов-теоретиков.
Случайные полезности
Homo oeconomicus, совершая тот или иной выбор, не всегда с полной определенностью знает его последствия. Это относится и к потребительскому выбору. Вы приобрели фарфоровую чашку и желаете насладиться ее красотой, но назавтра после покупки случайно поставили ее мимо стола, и покупка оказалась “менее полезной”, чем вы рассчитывали.
Или вы купили арбуз, и он оказался гораздо вкуснее, чем можно было подумать по его виду. Но все могло случиться по-иному: чашка могла бы служить вам много лет и ее ценность повышалась бы, а арбуз мог оказаться невкусным. Полезность покупки могла оказаться той или иной и из-за изменения условий ее использования (классический пример в новелле О’Генри “Дары волхвов”). Помимо этих эпизодов человек сознательно совершает ряд действий, результаты которых носят случайный характер. Он участвует в лотереях и играет в азартные игры. Он страхует свою жизнь и свое имущество, регулярно внося страховую плату и надеясь, что с ним не произойдет “страховой случай”, но не исключая такой возможности. Теория игр, созданная в 20-е гг. одним из самых блестящих ученых XX в. Джоном фон Нейманом, рассматривала поведение “игрока” в условиях, когда последствия его “хода” полностью не определяются его выбором. Более того, оказалось, что игрок, стремящийся к максимальному выигрышу, при определенных условиях должен делать случайные ходы. Теория игр породила новые подходы к анализу поведения экономического субъекта. Основные теоретические результаты в этом направлении были изложены Джоном фон Нейманом и Оскаром Моргенштерном в фундаментальном труде “Теория игр и экономическое поведение”, вышедшем в свет в 1943 г. (в русском переводе в 1970 г.).
Основное допущение, принятое Дж. фон Нейманом и О. Моргенштерном, состоит в том, что потребитель и в случайных ситуациях ведет себя рационально. А это значит, что, производя свой выбор, он сопоставляет не только варианты с однозначными исходами, но и такие варианты, исходы которых имеют случайную полезность. В последнем случае потребитель должен знать как все возможные исходы, так и их вероятности.
Оказалось, что в таком допущении содержится все необходимое для существования количественной меры полезности.
Авторы приводят такой пример. Некто предпочитает стакан чая (Ч) чашке кофе (К), а чашку кофе — стакану молока (М). Допустим, что он поставлен перед выбором: чашка кофе или стакан с неизвестным содержимым, которое с равными вероятностями может оказаться чаем и молоком. Если субъект выбрал кофе, это значит, что из двух предпочтений (Ч > К) и (К > М) второе оказалось более значимым. Следовательно, по своей полезности кофе ближе к чаю, чем к молоку. Если бы он выбрал стакан с неизвестным содержимым, это позволило бы сделать противоположный вывод. Если, наконец, ему безразлично, какую из двух возможностей выбрать, то это означает, что оба предпочтения, Ч > К и К > М, для него равноценны и полезность чашки кофе находится ровно посредине между полезностями стакана чая и стакана молока. Как мы уже видели, возможность сравнивать пары благ или их наборов — это уже основание для построения количественной шкалы полезностей.
Как могут сравниваться между собой численные значения полезностей решений, если каждое из них может иметь различные исходы с разными вероятностями?
Рассмотрим самый простой случай. Допустим, что некоторый выбор влечет за собой два возможных исхода, дающих выигрыш в размере u1 и u2 соответственно. Вероятности исходов могут быть неодинаковыми. Допустим, что выбор был произведен N раз, и при этом N1 раз наступил первый исход, а N2 = N – N1— второй. Тогда общая сумма выигрыша равна N1u1 + N2u2 а для одного акта выбора выигрыш в среднем равен:
| u = (N1u1 + N2u2)/N = au1 + (1 – a)u2, |
где a = N1/N— доля первого исхода, 1 – a = N1/N— доля второго исхода. При большом числе повторений и мало отличаются от вероятностей каждого исхода. Взяв величину равной вероятности первого исхода, мы можем рассматривать величину и как меру случайного выигрыша. Например, если величины выигрыша равнялись 20 и 10 единиц с вероятностями 0.6 и 0.4, то и = 0.6 • 20 + 0.4 • 10= = 16 единицам.
В более общем случае, если m возможных исходов дают выигрыши u1, u2,..., um с вероятностями (так что), в качестве числовой меры случайного выигрыша мы могли бы принять:
| u = a1u1 + a2u2 + … +amum. |
Показатель такого вида называется математическим ожиданием и играет важную роль в теории вероятностей. Заметим, что математическое ожидание случайного выигрыша зависит и от выигрышей при различных исходах, и от вероятностей каждого из них. Если, как и раньше, выигрыши равны 20 и 10 единицам, а вероятность а пробегает все значения от 0 до 1, то математическое ожидание принимает все значения от 10 до 20 единиц. И если у нас есть вариант выбора с фиксированным (не случайным) промежуточным выигрышем, скажем, 14 единиц, то можно подобрать такую вероятность a, что случайный выигрыш окажется равноценным рассматриваемому фиксированному (как легко проверить, в данном случае a = 0.4).
Лотерея как средство измерения полезности
Как мы видели, ординалистский подход к полезности вовсе не запрещает ее количественного выражения; он допускает большое разнообразие шкал, требуя от них лишь взаимной монотонности. Именно этот произвол в выборе шкал, при котором требуется лишь, чтобы переход от одной шкалы к другой не нарушал порядка (т. е. чтобы деления на линейках рис. 9 не были перепутаны), и означает, что мы имели дело с порядковой полезностью.

Рис. 9. Ординалистская функция полезности. Кривым безразличия могут быть присвоены числовые значения с помощью любой монотонной шкалы. Все изображенные на рисунке линейки в равной степени пригодны для этой цели.
Допустим ли такой же произвол в случае, когда наш выбор может иметь случайные исходы, а в качестве числовой меры случайного исхода используется показатель типа математического ожидания? Легко убедиться, что нет. Сравним два варианта выбора. Первый приводит к случайному результату с двумя исходами А и В (рис. 10), имеющими равные вероятности 0.5 и 0.5; второй — к промежуточному (по предпочтениям) неслучайному результату С.
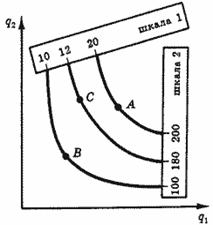
Рис. 10. Случайная полезность в разных шкалах
Допустим, что в некоторой шкале u1(А) = 20, u1(B)= = 10 и u1(С) = 12. Полезность первого варианта выбора определяется величиной 0.5•20 + 0.5•10= =15, и он предпочтительнее второго, полезность которого в этой шкале всего 12 единиц.
Теперь рассмотрим иную шкалу, в которой u1(А) = 200, u2(В) = 100 и u2(С) = 180.
Порядковые отношения, устанавливаемые этой шкалой, совпадают с предыдущей. Но в ней полезность первого выбора равна 0.5•200 + 0.5•100=150 единиц, и в этой шкале он уступает второму.
Мы пришли к противоречивому результату, а это значит, что, имея дело со случайными последствиями решений и используя для их оценки математические ожидания полезностей, мы не можем выбирать для измерения полезностей шкалы, согласованные друг с другом только в отношении порядка. Какая-то из рассмотренных нами шкал, а может быть, и обе, не годятся для представления случайных полезностей. Дж. фон Нейман и О. Моргенштерн разработали систему аксиом количественной полезности. Из этих аксиом следует существование такой функции полезности, математическое ожидание значений которой согласовано с предпочтениями субъекта.
А раз такая функция существует, можно представить себе инструмент для измерения ее значений. Всякое измерение есть сравнение с эталоном. В нашем случае в качестве эталона следовало бы выбрать такую вещь, приобретение которой вело бы к случайным результатам, сильно различающимся по полезности. Идеальным примером подобной вещи служит лотерейный билет: покупатель, изучив условия лотереи, знает, какие в ней разыгрываются призы и может оценить вероятность получения каждого из них.
Единственное, чего он не знает, достанется ли ему выигрыш.
Ситуация, рассмотренная нами выше и иллюстрируемая рис. 10, может рассматриваться как дилемма, стоящая перед потребителем: купить ли ему вполне определенный набор благ С или билет беспроигрышной лотереи, в которой разыгрывается поровну “хороших” наборов А и наборов “похуже” В. Аксиома рациональности в теории Неймана—Моргенштерна утверждает, что потребитель в состоянии решить, какой из покупок — набору С или лотерейному билету — он отдает предпочтение. Рассмотрим теперь лотерею, в которой разыгрываются два приза: соответствующий самому высокому уровню удовлетворения потребностей субъекта Х (“хороший”) и самому низкому П (“плохой”). Произвольно установим значения функции полезности U(П) = 10, U(X) = 20.
Оказывается, мы тем самым однозначно установили значения функции полезности для всех наборов благ. Допустим, что потребитель сравнивает приобретение некоторого конкретного набора благ с участием в такой лотерее. Если вероятность выигрыша Х велика (а вероятность 1 — выигрыша П мала), то он, пожалуй, предпочтет лотерею. Если же величина слишком мала, то он откажется от лотереи в пользу набора С. При некотором промежуточном значении вероятности, обозначим его, оба варианта окажутся равноценными. Если считать, что U(Q) —та самая функция полезности, существование которой следует из принятых аксиом, то должно выполняться равенство:
| U(C) = aCU(X) + (1 – aC)U(П) = 20aC + 10(1 – aC), |
а это значит, что мы однозначно определили полезность набора С. Так, если aC = 0.6, то U(C) = 16, как в одном из рассмотренных выше примеров. Мы выбрали призы Х и П таким образом, что любой набор благ окажется промежуточным (в смысле порядка). Поэтому для любого набора благ можно подобрать соответствующее значение вероятности, при котором лотерея с точки зрения субъекта не лучше и не хуже этого набора, и описанная нами процедура однозначно определила бы числовое значение полезности любого набора.
Напомним, что значения U(X) и U(П) мы назначили произвольно. Но, закрепив их, мы уже однозначно задали всю шкалу полезностей. Придавая произвольное значение U(П) = a и любое, но обязательно большее, значение U(X) = а + b, мы для набора С получили бы значение полезности:
| U(C) = aC(a + b) + (1 – aC)a = a + baC. |
Таким образом, все шкалы различаются между собой только значением свободного члена а (это может быть любое число) и коэффициента пропорциональности b (это может быть любое положительное число). Иными словами, любая шкала полезности по Нейману—Моргенштерну может быть получена из любой другой с помощью линейного преобразования — изменения начала отсчета и масштаба. Наиболее естественной представляется шкала, в которой U(П) = 0, U(X) = 1. Здесь полезность любого набора совпадает с вероятностью выигрыша “хорошего” приза в “безразличной” лотерее, U(C) = aC.
Теория полезности Неймана-Моргенштерна возникла тогда, когда в экономической науке уже утвердилось представление о том, что порядковая полезность достаточно полно описывает поведение потребителя. Новый взгляд, требовавший возврата (хотя и на ином уровне) к количественной полезности, естественно, вызвал активную дискуссию в ученом мире. К настоящему времени сферы применения обоих подходов в основном разделились.
Там, где имеется однозначная связь между выбором и его последствиями, вполне достаточен ординалистский подход, и в наших дальнейших лекциях мы ограничимся порядковой полезностью. Но в тех задачах, где нужно учесть случайный характер этой связи, требуется количественное измерение полезности.
РАЗДЕЛ 4. Как тратили деньги советские люди
Рациональное распределение дохода является сложной проблемой для каждого из нас.
Теория, исследуя поведение потребителя, как вам уже известно из предыдущего изложения, наделяет его высокой степенью разумности и обдуманности поступков.
Однако личный опыт показывает, что мы далеко не всегда придерживаемся оптимальной модели поведения. Да это было бы и довольно странным. Очень уж много факторов сознательно и подсознательно надо учитывать при принятии решений о распределении тех доходов, которыми мы располагаем. Тем не менее если рассматривать поведение потребителя как массовое явление и попытаться проанализировать статистические данные, характеризующие однородные группы потребителей по доходам, то вполне возможно выделение определенных закономерностей.
Распределение населения по доходам дает возможность оценить объем каждой отдельной доходной группы, ее удельный вес в общей численности населения при анализе использования дохода в семьях с разным материальным достатком. Потребитель принимает решение о распределении средств не на основе совокупного дохода[1], а только той его части, которая поступает к нему в виде некоторой суммы денег после выплаты налогов и обязательных платежей, — так называемого располагаемого дохода.
Для оценки поведения потребителя правильнее анализировать использование располагаемого денежного дохода. Структура использования располагаемого дохода в семьях рабочих и служащих с различным материальным достатком приведена в табл. 1.
Таблица 1. Использование располагаемого дохода в семьях рабочих в служащих с различным материальным достатком в 1989 г. в СССР (в %)
| Все население | В т. ч. со среднедушевым совокупным доходом в месяц, руб. | |||||
| до 75 | 75-100 | 100-150 | 150-200 | свыше 200 | ||
| Располагаемый доход Из располагаемого дохода израсходовано: на питание на непродовольственные товары на алкогольные напитки на услуги прочие расходы Накопления семьи | 100,0 35,4 33,7 303 10,3 6,2 11,1 | 100,0 53,7 28,1 2,2 8,1 6,7 1,2 | 100,0 46,5 28,5 2,8 10,2 6,5 5,5 | 100,0 39,1 32,2 3,2 11,2 6,3 8,0 | 100,0 33,7 35,0 3,4 10,8 6,0 10,5 | 100,0 28,7 35,1 3,5 9,4 8,4 14,9 |
*Рассчитано по: Социальное развитие СССР. М., 1991.
Анализ приведенных в таблице данных позволяет сделать следующие выводы: с увеличением средне душевого дохода:
— падает доля расходов на питание (с 53.7 до 28.7 %);
— растет доля затрат на непродовольственные товары и алкогольные напитки (соответственно с 28.1 и 2.2 % до 35.1 и 3.5 %);
— увеличивается доля сбережений в бюджете (с 1.2 до 14.9 %);
— доля расходов на услуги и прочих расходов остается примерно одинаковой;
— абсолютная величина затрат увеличивается по всем статьям.
Интересно сравнить структуру расходов в СССР со структурой в какой-либо высокоразвитой стране, например в Англии. Структура расходов потребителей в Англии приведена в табл. 2. Статьи затрат в табл. 1 и 2 не полностью сопоставимы. Тем не менее сравнение дает возможность сделать некоторые выводы.
1. Доли расходов на питание и непродовольственные товары (последнюю можно грубо оценить как сумму долей расходов на обувь и одежду и на товары для дома и услуги) в Англии почти в три раза были ниже, чем в СССР.
2. В Англии значительно более высоки доли расходов на жилье, транспорт и связь, а также отдых, образование и развлечения (учтите, что в табл. 1 эти статьи являются частью “прочих расходов”); причем они превышают или близки по величине к долям расходов, указанным в пункте 1.
В чем причина различий в структуре расходов англичан и советских людей в 1989 г.? Не претендуя на исчерпывающее объяснение, отметим три наиболее важных фактора. Во-первых, это структура цен на товары и услуги (например, низкая квартирная плата в СССР и высокая в Англии). Во-вторых, различие в уровне реального дохода (средний англичанин мог позволить себе больше “излишеств”). И, в-третьих, степень насыщения рынка товарами и услугами (англичанин имел не только больше средств, но и больше возможностей для их использования).
Поведение потребителей по всем доходным группам можно представить функцией потребления, график которой приведен на рис. 11 (см. также рис. 21 к лекции 15).

Рис. 11. Функция потребления
На графике проведен луч ОА из начала координат под углом 45°. Если бы функция потребления совпадала с этим лучом, то это означало бы, что весь доход идет на потребление. Часть дохода, расположенная над функцией потребления А, но в пределах, ограниченных лучом ОА, представляет сбережения.
Самые бедные семьи, вероятно, не имеют накоплений, или, как говорят, имеют отрицательное или нулевое сбережение. Это означает, что они тратят ровно столько или даже больше, чем зарабатывают. К сожалению, имеющаяся статистика не позволяет оценить количественно долю данной группы населения.
Таблица 2. Структура расходов среднего потребителя в Англии в 1989 г. (в %)
| Статьи затрат | Доля в общих расходах |
| Питание Табак Одежда и обувь Товары для дома и услуги Алкоголь Отдых, образование, развлечения Жилье Топливо и энергия Транспорт и связь Прочие расходы | 12,4 2,6 6,3 6,8 6,3 9,6 15,5 3,6 18,4 18,5 |
*Рассчитано по: Annual Statistical Abstracts. 1991. Р. 246-247.
Наше население традиционно бульшую часть прироста доходов тратило, а не сберегало.
Однако эта тенденция за последние годы резко усилилась. Так, если за период с 1980 по 1985 г. “средний” потребитель 67.5 % прироста дохода направлял на потребление, то в следующие 5 лет доля потребления в приросте дохода возросла до 86.2 %. Причем в 1990 г. практически все увеличение дохода, 98.9 %, было истрачено в этом же году (рассчитано по: Народное хозяйство СССР в 1990 г. М., 1991. С. 95.).
Указанные изменения вполне закономерны. Склонность к сбережению и потреблению взаимосвязаны. В условиях относительно устойчивого состояния экономики сбережения накапливались и сохранялись длительное время, что не приводило к резким изменениям в распределении дополнительных доходов. Углубление кризисной ситуации во второй половине 80-х гг., сопровождаемое усилением инфляционных процессов и незащищенностью вкладов от обесценивания, привело к резкому увеличению доли потребления. Хотя в действительности за ростом потребления скрыта попытка людей спасти свои увеличивающиеся доходы от обесценивания путем покупки всевозможных доступных им видов товаров впрок.
Так, по данным опроса городского населения, проведенного ВЦИОМ в августе 1991 г., почти 60 % опрошенных стараются сделать запасы продуктов питания и 40 % покупает впрок одежду, обувь, предметы культурно-бытового назначения (Потребительское поведение населения в кризисных ситуациях // Вопр. экономики. 1992. № 1. С. 74—82.).
Причем склонность к накопительству значительно выше в семьях с более высокими доходами. Практическое отсутствие других каналов расходования личных доходов заставляет людей с высоким материальным уровнем достатка спасать свои сбережения, обращаясь на потребительский рынок.
Своеобразным видом сбережения становится приобретение таких товаров, как ювелирные изделия, антиквариат, меха, машины, дачи и т. п. По данным того же опроса, наиболее популярными формами накопления средств в условиях нестабильности становится покупка конвертируемой валюты и драгоценных металлов.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 215; Нарушение авторских прав?; Мы поможем в написании вашей работы!