Разветвленные и неразветвленные магнитные цепи

Применение электромагнитных устройств постоянного и переменного тока в технике

МАГНИТНЫЕ ЦЕПИ

Несогласное залегание

Изучение геологических разрезов показывает, что соотношение между комплексами слоистых толщ горных пород бывает различным.

1. Каждый вышележащий слой или комплекс слоев разреза без каких либо следов перерыва в накоплении осадков налегает на предшествующий подстилающий слой. Полностью сохраняется стратиграфическая последовательность при накоплении слоев. Такое залегание называется согласным.

2. Возможно, что между вышележащими и подстилающими толщами нарушается стратиграфическая последовательность. Могут отсутствовать отложения тех или иных стратиграфических подразделений – стратиграфическое несогласие. Если при сохранении параллельности границ слоев из разреза выпадают те или иные стратиграфические горизонты говорят о параллельном стратиграфическом несогласии, свидетельствующим о перерыве в осадконакоплении. Поверхность размыва. Если при стратиграфическом несогласии выше и ниже лежащие слои обладают различными условиями залегания – угловое несогласие.

Магнитной цепью (магнитопроводом) называется совокупность различных ферромагнитных и неферромагнитных частей электротех­нических устройств для создания магнитных полей нужной конфигу­рации и интенсивности.

В различных областях техники широкое применение находят разнообразные электромагнитные механизмы и устройства, осуществляющие преобразование электрической энергии в механическую или создающие магнитные поля с необходимыми характеристиками.

К электротехническим механизмам постоянного тока можно отнести электромагнмтные и магнитоэлектрические реле, тяговые электромагниты (подъемные), а также магнитные цепи электричес­ких машин постоянного' тока и магнитные системы с постоянными магнитами.

К электротехническим устройствам переменного тока можно отнести электромагниты, реле, контакторы, трансформаторы, ин­дуктивные электромеханические преобразователи, дроссели, маг­нитные усилители, электрические машины переменного тока и т.д. В основе принципа действия их лежит использование свойств ферромагнитных материалов при возбуждении в них переменных во времени магнитных потоков.

Таким образом, в разного рода устройствах магнитное поле может возбуждаться либо постоянным магнитом, либо катушкой с током, расположенной в той или иной части магнитной цепи.

К простейшим магнитным цепям можно отнести тороид из однородного ферромагнитного материала (рис. 5.1)

Такие магнитопроводы применяются в многообмоточных тран­сформаторах, магнитных усилителях, в элементах ЭВМ и других электрических устройствах.

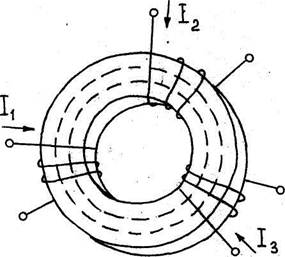
Рис. 4.1. Тороид

На рис. 4.2. изображена магнитная цепь электромеханичес­кого устройства, подвижная часть которого втягивается в электромагнит при постоянном.(или переменном) токе в катушке

Рис. 4.2. Электромеханическое устройство со втягивающимся сердечником

На рис. 4.3. изображена магнитная цепь, в которой магнит­ное поле возбуждается постоянным магнитом. Если подвижная катушка, расположенная на ферромагнитном цилиндре, включена в цепь постоянного тока, то на неё действует вращающий момент. Пово­рот катушки с током не влияет на магнитное поле магнитной цепи. Такая магнитная цепь есть в электроизмерительных приборах магнитоэлектрической системы.

Рис. 4.3. Магнитная цепь с постоянным магнитом

Рассмотренные магнитные цепи, как и другие возможные кон­струкции, можно разделить на неразветвленные магнитные цепи (рис..4.1, 4.3), в которых магнитный поток в любом сечении одинаков, и разветвленные магнитные цепи (рис.4.2), в которых магнитные потоки в различных сечениях цепи различны.

В большинстве случаев (кроме некоторых с допущениями, и определенными режимами работы) магнитную цепь считают нелиней­ной.

4 .3. Закон полного тока для магнитной цепи с постоянной магнитодвижущей силой

Этот закон получен на основании многочисленных опытов: ин­теграл от напряженности магнитного поля по любому контуру (цир­куляция вектора напряженности) равен алгебраической сумме то­ков, сцепленных с этим контуром.

(4.1)

Причём, положительными следует считать те токи, направле­ние которых соответствует обходу контура по направлению движе­ния часовой стрелки (правило буравчика). Так, для контура на рис. 4.4.

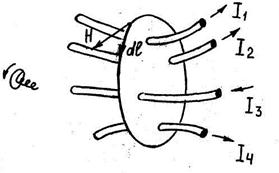Рис. 4.4. Контур магнитной цепи

Величина (в (4.1.)) называется магнитодвижущей силой (сокращенно МДС).

Основная единица измерения магнитодвижущей силы - ампер (А), для напряженности магнитного поля - ампер на метр (А/м), иногда - ампер на сантиметр (А/см), I А/см = 100 А/м. Магнит­ную цепь большинства электротехнических устройств можно пред­ставить состоящей из совокупности участков, в пределах каждо­го из которых можно считать магнитное поле однородным, т.е. с постоянной напряженностью, равной напряженности магнитного поля Н _к вдоль средней линии участка l_к. Для таких цепей можно заменить интегрирование в (4.1) суммированием. Если при этом магнитное поле возбуждается катушкой с током I, у кото­рой w витков, то для контура магнитной цепи, сцепленного с витками и состоящего из n участков, вместо (5.1) можно записать:

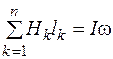
Если контур сцеплен с витками m катушек с токами, то

где F_p = I_p w _p - МДС.

Таким образом, согласно закону полного тока МДС F равна сумме произведений напряженноcтей магнитного поля на длины соответствующих участков для контура магнитной цепи.

Произведение Н_кl_к = U_мк часто называют магнитным напря­жением участка магнитной цепи.

4 .4. Катушка с магнитопроводом в цепи переменного тока

У катушки с магнитопроводом, подключенной к источнику си­нусоидального напряжения U = U_m sinw t (рис. 4.5,а) переменный ток i в обмотке возбуждает в магнитопроводе пере­менный магнитный поток Ф, который индуктирует в обмотке ЭДС самоиндукции

e_L = –w×(d Ф/ dt)

Если пренебречь активным сопротивлением обмотки и считать, что все магнитные линии поля катушки замыкаются только по магнитопроводу, то на основании 2 закона Кирхгофа для контура, обозначенного на рис. 4.5,а пунктиром, получим уравнение

U = –e_L (4.2)

или U = U_m sinw t = w× d Ф/ dt

Из этого уравнения найдём закон изменения во времени магнитного потока. Так как

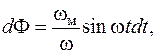
то .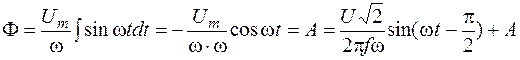

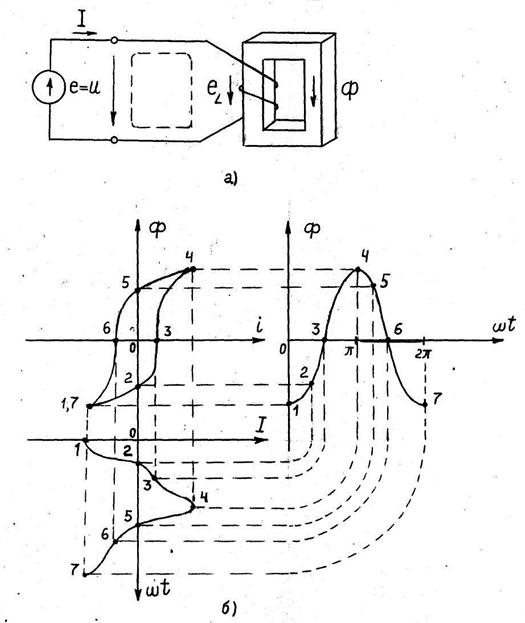
Рис. 4.5. Катушка с магнитопроводом (а), магнитные характеристики (б)

Постоянная интегрирования А равна некоторому постоянному магнитному потоку, которого нет в магнитопроводах аппаратов пе­ременного тока в установившемся режиме работы. Значит постоян­ная А = 0 и магнитный поток

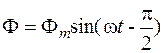
где Ф _m = U /4,44 f w Ф _m (4.3)

то есть, при синусоидальном напряжении между выводами катушки магнитный поток в магнитопроводе тоже синусоидальный.

Так как действующие значения напряжения U между вывода­ми катушки и ЭДС самоиндукции E_L одинаковые (4.2), то из (4.3) получим

E_L = 4,44 f w Ф _m

Последнее соотношение часто применяют для расчетов ЭДС, индукти­руемых в обмотках трансформаторов, поэтому его часто называют уравнением трансформаторной ЭДС.

Дата добавления: 2014-01-05