Стандартные матрицы

Довольно часто в линейной алгебре используются единичные матрицы, нулевые матрицы, матрицы все элементы которых равны константе (обычно одному).

В Matlab существуют функции для формирования таких матриц:

eye (n)- определяет единичную матрицу размером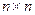

eye (m×n)- - определяет единичную матрицу размером 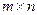с единицами в диагонали и с нулями в остальных элементах матрицы;

eye (size(M)) - определяет единичную матрицу с тем же размером, что и матрица М.

zeros(n)- создает матрицу размером 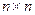с нулевыми элементами;

zeros(m,n)- - образует матрицу размером 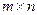с нулевыми элементами;

zeros(size(M))- - возвращает матрицу с нулевыми элементами того же размера, что и матрица М.

ones(n)- образует матрицу размером 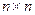, все элементы которой равны единице;

ones(m,n)- - образует единичную матрицу размером ;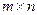

ones(size(M))- - образует единичную матрицу такого же размера, как и матрица М.

Примеры:

Для выделения элементов матриц используются индексы, заключенные в круглые скобки- Х(i,j), i –номер строки, j – номер столбца.

Для вызова на экран элементов вектора или матрицы достаточно указать их имя и координаты в круглых скобках (номер строки и номер столбца вектора).

Пример:

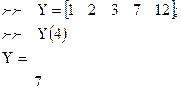
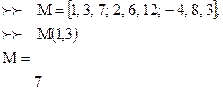
Для замены элемента необходимо указать имя элемента или матрицы, его координаты и присвоить этому имени новое значение элемента. После нажатия клавиши «ENTER» на экране будет отображен вектор или матрица с новым значением элемента.

Пример:

Пусть вектор и матрица – те же, что и в предыдущем примере. Заменим третий элемент вектора (со значением 3) на 12, а элемент матрицы, находящийся во второй строке и третьем столбце (со значением 12), - на -7.

Решение:

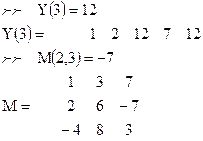
Изменение размера вектора проще всего осуществить путем его редактирования. Изменение размера матрицы легче выполнить посредством удаления или добавления строк и столбцов матрицы.

Удаление строки или столбца осуществляется с помощью знака двоеточия, который ставится в круглых скобках после имени матрицы:

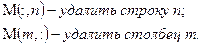
Пример:

Пусть матрица имеет вид:

Необходимо удалить вторую строку и третий столбец. Решение будет иметь вид:

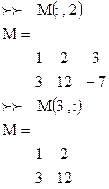
Увеличить размер матрицы можно посредством объединения малых матриц в большую. Эта процедура называется конкатенацией. Она осуществляется путем образования матрицы из имен малых матриц. При этом допускаются алгебраические операции над именами.

Пример:

Пусть имеется три следующих вектора:

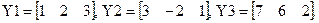
Образуем матрицу из этих векторов. Векторы следует рассматривать как элементы матрицы. Тогда получим:

На экране матрица из векторов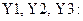

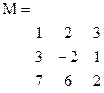
Перестановка столбцов и строк матрицы осуществляется с помощью следующих функций:

1) - осуществляет перестановку столбцов матрицы М относительно вертикальной оси;

2) - осуществляет перестановку строк матрицы относительно горизонтальной оси.

Пример:

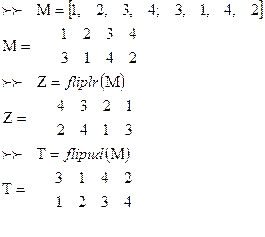
Поворот матрицы позволяет создать новую матрицу, у которой меняются не только значения элементов в строках и столбцах, но также размер матрицы.

Поворот матрицы осуществляет функция 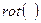, имеющая вид: 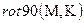, где:

М – матрица;

К - число, указывающее на величину поворота матрицы в градусах, кратных .

Если к=1, то поворот осуществляется на , при к=2 – на 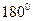и так далее.

Поворот выполняется против часовой стрелки. При к=1 функция имеет вид .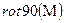

Пример:

Дата добавления: 2014-01-05