И граничных условиях. Определить максимум целевой функции

Определить максимум целевой функции

Задача распределения ресурсов

Является задачей линейного программирования (ЗЛП), которая формулируется следующим образом:

F(x) = c₁x₁ + c₂x_{2 +…+} c_nx_n = max

при ограничениях:

а₁₁х₁ + а₁₂х₂ + … +а_1n ≤ b₁

а₂₁х₁ + а₂₂х₂ + … +а_2n ≤ b₂

_{………………………………………….}

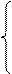аm₁х₁ + а_m2х₂ + … +а_mn ≤ b_m

x_j ≥ 0, j = 1…n

Пример: Фирма выпускает товары трёх видов - x₁, x₂ и x₃, используя ресурсы 1,2 и 3.

Каждая единица товара x₁ приносит прибыль в 3 руб., товара x₂ - 2 руб. и товара x₃ – 1 руб.

Потребности в ресурсах:

Ресурсы	x1	x2	x3	Склад
Ресурс 1			-
Ресурс 2		-
Ресурс 3			-

ресурса 1 требуется 1 ед. для выпуска товара x₁ и 1 ед. для выпуска x₂.

ресурса 2 требуется 1 ед. для выпуска товара x₁ и 1 ед. для выпуска x₃.

ресурса 3 требуется 2 ед. для выпуска товара x₁ и 2 ед. для выпуска x₂.

Всего на складе 12 ед. ресурса 1, 3 ед. – ресурса 2 и 16 д. ресурса 3.

Все товары - x₁, x₂ и x₃ ненулевые, т.е. x_i ≥ 0, j = 1…n.

Определить оптимальный план и распределение ресурсов по товарам для получения максимальной прибыли

Математическая модель ЗЛП примет вид:

F(x) = 3x₁ + 2x₂ + x₃ = max (1)

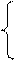x₁ + 2x₂ ≤ 12 (2)

x₁ + x₃ = 3 (3)- система ограничений

4x₁ + 2x₂ ≤ 16 (4)

Граничные условия:

x_j ≥ 0, j = 1…n

Решение:

1. Выразим x₃ из второго уравнения и подставим в ЦФ - (1):

x₃ = 3 - x₁;(5)

F(x) = 3x₁ + 2x₂ + x₃ = 3x₁ + 2x₂ + 3 - x₁ = 2x₁ + 2x₂ + 3 =max

Из (3) следует, что т.к. x₃ ≥ 0, то 3 - x₁ ≥ 0 или x₁ ≤ 3.

2. Тогда система ограничений примет вид:

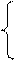x₁ + 2x₂ ≤ 12

x₁ ≤ 3 или - для уравнений в отрезках:

4x₁ + 2x₂ ≤ 16

.

Построим эти прямые на плоскости:

Получили многоугольник – область определения решений (заштрихован), в котором нужно найти точку, где ЦФ F(x) = max.

3. Построение вектора-градиента.

Из целевой функции F(x) = 2x₁ + 2x₂ + 3 берём коэффициенты при x₁ и x₂, получаем вектор С = (2, 2), который соединяет т.О (0, 0) с т. (2, 2). Вектор С показывает направление увеличения ЦФ F(x).

Проводим перпендикулярно вектору-градиенту прямую и перемещаем её по вектору до пересечения с последней вершиной многоугольника – это т. (1,2; 5,4), в которой х₁ = 1,2, а х₂ =5,4.

Тогда из (5) x₃ = 3 - x₁ = 3 – 1,2 = 0,8.

Тогда опорный план выпуска составит (1,2; 5,4; 0,8).

При таких данных целевая функция

F(x) = 3x₁ + 2x₂ + x₃ = 3,6 + 10,8 + 0,8 = 15,2.

Таким образом, прибыль в 15,2 руб. будет получена, если выпускать товар x₁ в количестве 1,2 шт, x₂ – в количестве 5,4 шт. и x₃ = 0,8 шт.

Подставляя значения опорного плана в систему ограничений (2-4), получим распределение ресурсов:

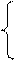x₁ + 2x₂ ≤ 12 или 1,2 + 10,8 = 12 – ресурс 1 истрачен полностью,

x₁ + x₃ = 3 или 1,2 + 0,8 = 2 – из ресурса 2 истрачено 2ед., осталось – 2 ед.,

4x₁ + 2x₂ ≤ 16 или 4,8 + 10,8 = 15,6– из ресурса 3 истрачено 15,6 ед.,

осталось - 0,4 ед.

Дата добавления: 2014-01-05