Нормирование диагностических параметров

Значительный объём определяющих параметров (несколько сотен), их различная физическая природа и, следовательно, широкий диапазон размерностей приводят к необходимости нормирования ДП. Введение нормированных, т.е. относительных параметров, или координат даёт единый аналитический инструмент для исследования достоверности диагностирования систем различного назначения.

Выполним нормирование подинтегральных выражений.

В качестве нормирующей величины измеренных значений х определяющего параметра Х используем его с.к.о. s_х и обозначим нормированное значение параметра через у:

(4.6)

Выполним нормирование случайной составляющей помехи e, взяв в качестве нормирующей величины с.к.о. s_e и обозначив нормированное значение через t:

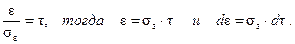(4.7)

Выполним нормирование пределов интегрирования.

В качестве нормирующей величины эксплуатационного допуска D на определяющий параметр Х также используем с.к.о. s_х и получим:

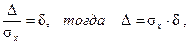(4.8)

где d – относительная величина эксплуатационного допуска.

При условии m_x = 0 нижняя граница допуска

a = – D = – s_x×d,

а её нормированное значение согласно (4.8) равно

a /s_x = – D /s_x = – d.

При том же условии верхняя граница допуска b = D = s_x×d, а её нормированное значение равно b /s_x = D /s_x = d.

Нормированные значения пределов интегрирования случайной составляющей помехи e при условии m_x = 0 находим с учётом (4.6 – 4.8) из следующих соотношений:

для e = а – x = – D – x = – s_x×d – s_x× у = s_x×(­– d – у);

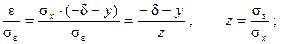
для e = b – x = + D – x = s_x×d – s_x× у = s_x×(­ d – у);

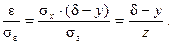
Отношение с.к.о. помехи и параметра назовём приведенной погрешностью измерения диагностического параметр Х.

С учётом приведенных зависимостей запишем расчётные зависимости ошибок контроля первого и второго рода как функции нормированных параметров:

(4.8)

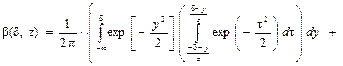
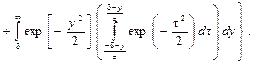(4.9)

Лабораторні дослідження впливу характеристик визначального процесу, а саме:

– відносного значення експлуатаційного допуску d,

– зведеної похибки вимірювання параметра z та

– кратності n вимірювання визначального параметра

на ймовірності a та b формування помилкових рішень рекомендується виконувати на основі аналітичних залежностей, запозичених з роботи [3], що враховують всі три характеристики діагностичного процесу:

,

.

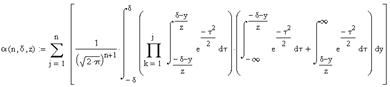Дата добавления: 2014-01-05