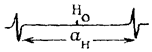Условия парамагнитности частиц с неспаренными электронами

Парамагнетизм – свойство частиц, имеющих магнитный момент, намагничиваться во внешнем магнитном поле в направлении силовых линий этого поля (пара от греч. – изменение, отклонение, общий, совокупный).

ЭПР наблюдается только для парамагнитных частиц, для которых суммарное спиновое квантовое число всех электронов в частице (молекуле, атоме, радикале) не равно 0. Число спиновых состояний электронов в частице определяется равенством:

N = 2 S_общ + 1,

где S_{общ =} åm_е.

Для обычной органической молекулы åm_е = 0, поскольку принцип Паули дозволяет на одной электронной орбитали находиться только 2 электронам с противоположными спинами - ½ и + ½, поэтому сумма спинов равна 0. При этом N = 1 (основное синглетное состояние S_o)., сигнал ЭПР не наблюдается, ибо нет 2-х состояний, между которыми происходили бы переходы.

Если частица имеет 1 неспаренный электрон, т.е. åm_е = + ½ или - ½, тогда N = 2 (дублетное состояние). Таким образом, имеется два состояния (ориентация по полю и против поля), между которыми возможны переходы, вследствие чего наблюдается сигнал ЭПР.

Если частица имеет 2 неспаренных электрона, то åm_е­ = 1, а N = 3 (триплетное состояние, когда неспаренные электроны имеют параллельные спины). Здесь переходы, естественно, возможны и ЭПР наблюдается.

Чтобы наблюдался ЭПР, необходимо, чтобы N > 1, т.е. частица в этом случае парамагнитна, отсюда и термин ЭПР.

Условия парамагнитности частиц:

· Атомы или ионы с незаполненными внутренними электронными оболочками (например, ионы ионы переходных металлов).

· Атомы или молекулы с неспаренными электронами: Н^·, Cl^·, ^·NO, ^·NO₂, ^·O-O^· и тому подобное.

· Свободные органические радикалы R^·: СН₃^· и тому подобное.

· Возбужденные триплетные состояния.

· Металлы, полупроводники.

5.4. Спектры ЭПР. Число полос N = 2I_cn_c + 1.

5.4.1. Спектр ЕПР SО₃^·-.

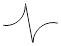Спектр ЭПР анион-радикала SО₃ представляет собой синглет:

5.4.2. Спектр ЕПР атома Н^·.

Здесь спин электрона взаимодействует со спином протона, N = 2×½×1 + 1 и наблюдается дублет:

а_Н – константа сверхтонкого взаимодействия

Для Н˙ а_Н =506,8 гс (эквивалентно 1420,4 МГц).

Наблюдается так называемое сверхтонкое взаимодействие. Тонкое взаимодействие, при котором также имеет место расщепление линии, возникает в кристаллическом поле даже при отсутствии Н_о (расщепление в нулевом поле), которое здесь рассматриваться не будет.

5.4.3. Спектр ЕПР атома D^·.

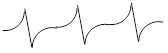N = 2 + 1 = 3. Здесь наблюдается триплет с линиями одинаковой интенсивности:

5.4.4. Спектр ЕПР СН₃^·.

N = 2×½×3 + 1 = 4.. Соотношение интенсивности линий определяют по треугольнику Паскаля для І =1/2.

5.4.5. Спектр ЕПР СD₃^·, N = 7. Соотношение интенсивности линий определяют по треугольнику Паскаля для І = 1:3:6:7:6:3:1.

5.4.6. Спектр ЕПР радикала ^·

СН₂ОН:

5.4.7. Спектр ЕПР бутильного радикала.

СН₃СН₂СН₂СН₂^· Здесь электроны с протонами в d-положении уже не

d g b a взаимодействуют. Для других положений наблюдается

следующее соотношение между константами сверхтон- кого взаимодецйствия: а_β > а_α >> а_γ. Число полос в мультиплете и соотношение их интенсивностей определяется числом атомвв водорода α, β и γ положениях.

Распределение электронов по ядрам водорода в разных положениях можно охарактеризовать спиновой плотностью электрона на ядре водорода:

r_н = a_н(R^·)/a_н(Н^·) = a_н(R^·)/506,8.

Спиновая плотность не спаренного электрона на ядре протона в пропиле CH₃CH_2­CH₂· в различных положениях показана ниже:

положения α β γ

a_H(гс) 22,1 30,3 0,3

ρ_Н 0,04 0,06 0,0006

5.4.8. Спектр ЕПР анион-радикала бензола С₆Н₆^·ˉ.

Спектр содержит 7 линий с соотношением их интенсивности в соответствии с треугольником Паскаля - 1:6:15:20:15:6:1.

5.4.9. Сложные спектры.

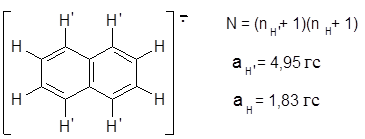5.4.9.1. Спектр анион-радикала нафталина.

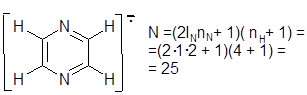5.4.9.2. Спектр анион-радикала пиразина.

5.4.9.3. Спектр анион-радикала 1,4,5,8-тетраазанафталина.

Задание для СРС: графически построить спектр для анион-радикала нафталина (масштаб произвольный).

Дата добавления: 2014-01-05