Модуль объемной деформации и модуль сдвига

Изложенное выше показывает, что для описания процесса деформирования грунта с использованием модели линейно деформируемой среды достаточно знать две деформационные характеристики: модуль деформации Е и коэффициент Пуассона v, которые могут быть вычислены по результатам экспериментальных исследований. Эти характеристики обычно применяются при решении одномерной задачи компрессионного уплотнения. В общем случае при решении плоской и пространственной задач бывает удобно любую деформацию грунта представить в виде суммы объемных деформаций и деформаций сдвига. При этом используются другие деформационные характеристики грунта: модуль объемной деформации К и модуль сдвига G, которые могут быть определены следующим образом.

Преобразуем правую часть первого уравнения системы (6.9), добавляя к ней со знаками плюс и минус член vσ_x/E, тогда получим

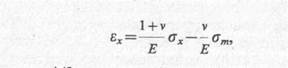
где σ_т = (σ_х + σ_у + σ_z)/3.

Теперь, вновь добавляя к этому выражению с разными знаками член (1 + v)σ_m/E, получим

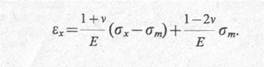
Поступая аналогично с остальными уравнениями этой системы, обобщенный закон Гука можно представить в виде

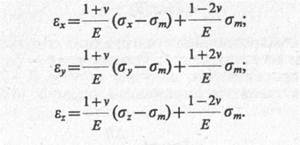(6.16)

Здесь первые члены правой части уравнений характеризуют деформации сдвига (формоизменения грунта), а вторые — объемные деформации. Действительно, если определить из этих выражений значение объемных деформаций ε_ν=ε_х+ε_у+ε_z то сумма первых членов правых частей будет равна нулю, т. е. при действии только нормальных напряжений деформации формоизменения отсутствуют. Тогда уравнения (6.16) можно записать в виде

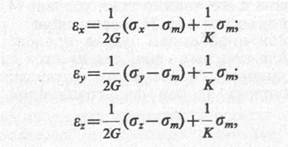(6.17)

где

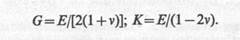(6.18)

Отсюда легко выразить коэффициент Пуассона через модуль объемной деформации и модуль сдвига:

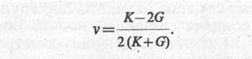(6.19)

Таким образом, зная из опыта любую пару деформационных характеристик грунта Е и v или К или G, можно по приведенным выше формулам определить остальные характеристики. Зная модуль сдвига G, можно определить горизонтальные перемещения (сдвиги) сооружений на грунтовых основаниях под действием горизонтальных сил.

Дата добавления: 2014-01-05