Расчет параметров логистической функции

Логистическая функция y = 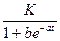приводится к линейному виду путем целого ряда преобразований:

1) Вначале обе части равенства обращаются:

=

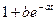
2) Вычитая 1 из обеих частей уравнения, получаем:

-1 =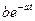

3) Логарифмируя, получаем:

ln(-1)= lnb - at

4) Вводим новые переменные:

z = ln(-1) и B = lnb

5) Получаем уравнение парной линейной регрессии:

z = B - at

После расчета его параметров, выполняем все необходимые обратные преобразования переменных.

3й учебный вопрос: Причины нарушения и способы проверки предпосылок метода наименьших квадратов (МНК) при построении нелинейных уравнений регрессии.

Следует иметь ввиду, что при расчете параметров нелинейных по параметрам, но внутренне линейных моделей, метод наименьших квадратов применяется к преобразованным уравнениям. Если при оценке параметров линейных моделей и моделей, не линейных по факторным переменным, применение МНК основано на использовании критерия min S (y-y_c)², то при оценке параметров моделей, не линейных по параметрам, критерий минимума квадратов используется по отношению к преобразованным значениям результативной (зависимой) переменной y (т.е. их логарифмам, обратным значениям и т.д.)

При использовании таких процедур линеаризации, которые затрагивают преобразование зависимой переменной, необходимо проверять выполнение предпосылок метода наименьших квадратов (МНК), так как они могут нарушаться при преобразовании.

Например, для линейных уравнений регрессии обычно выполняется условие S (y-y_c)=0, т.е. сумма отклонений фактических значений у от расчётных, равна 0. (Расчётные y_c - это те, которые рассчитаны по построенному уравнению регрессии: y_c =a₀ + a₁x)

Однако в нелинейных уравнениях регрессии эта сумма может отличаться от нуля, так как после логарифмирования мы применяем МНК к логарифмам переменных, то есть будет выполняться условие:

å(ln y – ln y_x) =0, но при этом вообще говоря, å(y-y_c)¹0

Это будет нарушением одной из предпосылок, на которых основано использование МНК. Рассмотрим более подробно все предпосылки МНК и те процедуры, которые используются для их проверки.

Как уже отмечалось на предыдущей лекции, при использовании МНК проводятся специальные статистические проверки значимости (достоверности, надежности) построенных уравнений и их отдельных параметров с помощью различных статистических критериев (Фишера, Стьюдента и др.)

Применение этих критериев основано на определенных предположениях о поведении остатков ε_i =y – y_i. Предполагается, что эти остатки остаются независимыми случайными величинами, а их среднее значение равно нулю. Они имеют постоянную дисперсию и подчиняются закону нормального распределения.

Проверка наличия у остатков этих предполагаемых свойств проводится уже после построения уравнения регрессии.

Проверка этих свойств сводится к тому, что оценки параметров должны быть:

а) несмещенными;

б) состоятельными;

в) эффективными.

1. Несмещённость оценки параметров регрессии означает, что математическое ожидание (средняя величина) остатков равна нулю, т.е. при очень большом числе наблюдений остатки не будут накапливаться и увеличивать ошибку аппроксимации.

2. Эффективность – наличие минимальной дисперсии остатков, что позволяет перейти от точечного оценивания параметров к интервальному.

3. Состоятельность – это увеличение точности оценок параметров при увеличении объёма выборки, т.е. числа наблюдений n, иначе говоря, вероятность того, что ожидаемые значения параметров регрессии окажутся в заданном интервале, стремится к 1 при n, стремящемся к бесконечности.

Условия необходимые для получения несмещённых, эффективных и состоятельных оценок параметров регрессий представляют собой те предпосылки МНК, о которых мы говорили на предыдущих лекциях.

Их соблюдение желательно для получения достоверных результатов расчетов по регрессионным моделям.

Перечислим еще раз пять основных предпосылок МНК.

1. Случайный характер остатков.

2. Средняя величина остатков равна 0 и не зависит от х.

3. Гомоскедастичность (дисперсия остатков постоянная и не зависит от х)

4. Отсутствие автокорреляции остатков.

5. Остатки подчиняются нормальному закону распределения.

Для проверки первой предпосылки нужно построить график зависимости остатков от расчетных значений y_xi.

Если получаемые точки на графике размещаются в некоторых пределах, образовывающих горизонтальную полосу, то E_i носят случайный характер.

Если график имеет другой вид, это означает, что остатки не случайны или имеют постоянную дисперсию.

Для проверки второй предпосылки просто рассчитывается сума остатков, так как если их сумма равна), то и их средняя величина тоже (S (g-g_c))/n=0

Для проверки третьей предпосылки надо построить графики зависимости E_i от различных факторов x_j.

На графике тоже должна получиться горизонтальная полоса.

Если график имеет другой вид, то остатки не являются гомоскедастичными, следовательно, имеет место гетероскедастичность остатков. Если остатки гетероскедастичные, то обычный МНК применять не имеет смысла. В эконометрике используется обобщённый МНК, который применяется к преобразованиям данным. Каждую переменную x_j делят на некоторый коэффициент пропорциональности k_j.

Для проверки четвёртой предпосылки (т.е. отсутствия автокорреляции уровней ряда остатков) используют критерий Дарбина-Уотсона).

Критерий Дарбина-Уотсона связан с проверкой гипотезы об отсутствии автокорреляции первого порядка, т. е. автокорреляции между соседними остаточными членами ряда. Значение критерия определяется по формуле

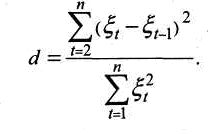
Можно показать, что

где r - коэффициент автокорреляции первого порядка (парный коэффициент корреляции между двумя последовательностями остатков)

Статистику Дарбина-Уотсона можно преобразовать следующим образом

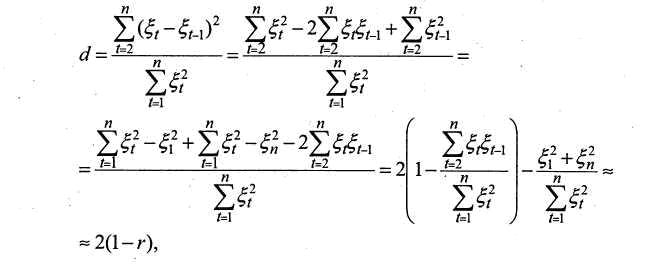
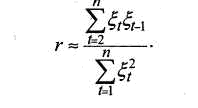
Из полученного выражения для статистики Дарбина-Уотсона видно, что при значении статистики d, близком к нулю, (коэффициент корреляции близок к 1), наблюдается высокая положительная автокорреляция; близость значения статистики d к 4 означает наличие высокой отрицательной автокорреляции (коэффициент корреляции близок к 1).

В случае отсутствия автокорреляции значение статистики будет близким к 2 (коэффициент корреляции близок к 0).

Расчетное значение статистики d сравнивается с граничными значениями (d₀ - верхняя и d₁- нижняя границы). В табл. 6.1 приведен фрагмент таблицы, в которой показаны в зависимости от числа наблюдений n граничные значения d₀ и d₁критерия Дарбина-Уотсона при уровне значимости а=0,05.

На рис. 6.1 и 6.2 приведены алгоритмы выявления автокорреляции остатков с использованием критерия Дарбина-Уотсона.

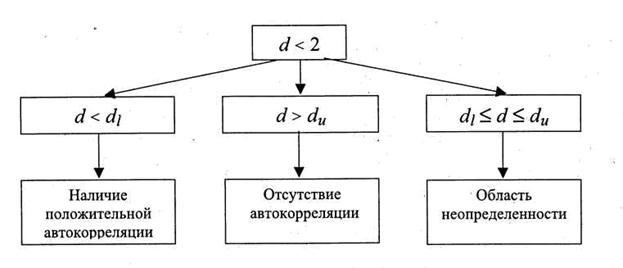
Рис. 6.1. Алгоритм выявления положительной автокорреляции остатков

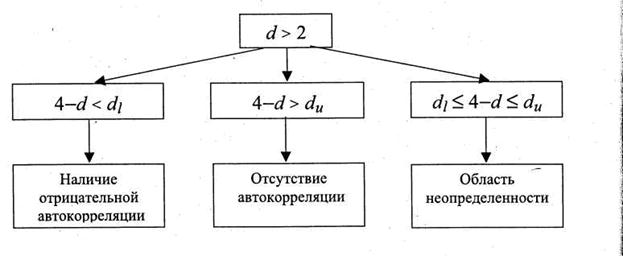
Рис. 6.2. Алгоритм выявления отрицательной автокорреляции остатков

Таблица 6.1.

Дата добавления: 2014-01-05