Структурная организация ЦПЭ

План.

Сложные суждения.

1.Простые и сложные суждения, их виды.

2.Отношения между простыми суждениями.

3.«Логический квадрат» и его задачи.

4.Таблица истинности сложных суждений.

5.Отрицание простых и сложных суждений.

6.Отношения между сложными суждениями.

Сложные суждения состоят из простых суждений, связанных логическими союзами: конъюнкцией, дизъюнкцией, импликацией и эквиваленцией.Но об этом позже, вначале рассмотрим простые суждения и их истинностные значения.

Ознакомившись с простыми суждениями, мы уже знаем, что основной логической характеристикой суждения является истинностное значение. Соответственно, логический анализ суждений разворачивается по поводу их истинности или ложности. Понятно, что сделать это в сложных высказываниях значительно трудней, чем в простых. Чтобы выполнить эту задачу, нужно учесть специфику логического анализа сложных суждений. Она состоит в следующем:

1. Истинностные значения сложных суждений зависят от двух параметров: истинностных значений составляющих их простых суждений (а) и характера логических союзов (б).

1. В простых суждениях, входящих в состав сложных, учитываются только их истинностные значения. Внутренняя (субъектно-предикатная) структура простых суждений, а также их качество и количество не учитываются.

2. В простых суждениях, входящих в состав сложных, учитываются только их истинностные значения. Внутренняя (субъектно-предикатная) структура простых суждений, а также их качество и количество не учитываются.

3. Истинностные значения сложных суждений определяют путём составления таблиц истинности.

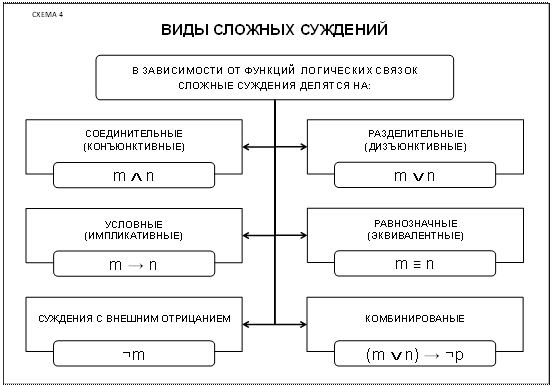ВИДЫ СЛОЖНЫХ СУЖДЕНИЙ. В зависимости от функций логических союзов различают конъюнктивные, дизъюнктивные, импликативные, эквивалентные, отрицательные и комбинированные суждения (схема 4).

Также как и понятия, суждения могут находится в различных отношениях между собой. Два любых простых суждения по их логической форме могут быть сравнимыми и несравнимыми.

Несравнимыми называют суждения, в которых различны субъекты или предикаты. Например, рассмотрим два суждения «Тюремное заключение является уголовно-правовой санкцией» и «Ссылка является уголовно-правовой санкцией». У этих суждений различные субъекты и одинаковые предикаты – при этих условиях их нельзя поставить в явную логическую зависимость и тем самым установить отношение между ними.

Сравнимыми называют суждения, имеющие одинаковые термины – субъект и предикат – и различающиеся лишь по количеству или качеству. Например, суждения «Все банки являются государственными» и «Некоторые банки не являются государственными» можно сравнивать, ибо они имеют одинаковый субъект и предикат (или иначе говоря, имеют «одинаковую материю») и отличаются по количеству и качеству.

Среди сравнимых суждений различают совместимые и несовместимые суждения.

Совместимость бывает трех видов: полная совместимость (эквивалентность)Аº А, ЕºЕ, ОºО, IºI; частичная совместимость (субконтрарность) I- O и логическое подчинение (субординация) A –I, E- O.

Несовместимость бывает двух видов: противоположность (контрарность) А-Е и противоречивость (контрадикторность) А-О, Е-I.

Отношения между простыми суждениями иллюстрируются при помощи наглядной схемы, называемой «логическим квадратом». Три основных задачи выполняет «логический квадрат»:

1. Служит для мнемонического запоминания логических отношений между простыми категорическими суждениями А (общеутвердительным), Е (общеотрицательным), О (частноотрицательным) и I (частноутвердительным). «ЛОГИЧЕСКИЙ КВАДРАТ» – это схема, облегчающая запоминание отношений между простыми категорическими суждениями с одинаковыми терминами; придумана она византийским историком и логиком Михаилом Псёллом (1018–ок.1096).

Вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними.

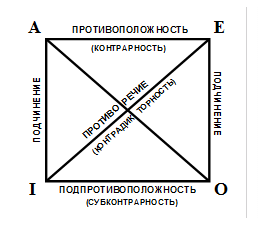
2. Вторая задача «логического квадрата» характеризуется тем, что можно чисто теоретически, не обращаясь к практике, исходя из истинности или ложности исходного суждения, показать какими – истинными, ложными, неопределенными – будут остальные три суждения, находящиеся с ним в определенных отношениях.

Самым простым является отношение подчинения, существующее между общими и частными суждениями Е-О, А- I. Общее суждение А или Е называется подчиняющим, соответствующее частное суждение I или О называется подчиненным. Если общее суждение истинно, то подчиненное частное суждение также истинно, но обратное неверно: если подчиненное суждение истинно, то подчиняющее общее суждение может быть как истинным, так и ложным. Например, если суждение «Все караси – рыбы» истинно, то будет истинно и подчиненное частное суждение «Некоторые караси рыбы». Если же истинно частное суждение «Некоторые слоны живут в Африке», то общее суждение «Все слоны живут в Африке» может быть как истинным, так и ложным, то есть неопределенным (суждение нужно рассматривать в конкретной рассматриваемой ситуации). Ложность частного суждения определяет и ложность общего суждения («Некоторые люди могут жить без воздуха» – ложно, ложно и общее суждение «Все люди могут жить без воздуха»), ложность общего суждения оставляет частное суждение неопределенным («Все люди добрые» – ложь, «некоторые люди добрые» –0 неопределенно, надо рассмотреть, о каких конкретно людях идет речь.

Между суждениями А и Е – отношения противоположности (контрарности): эти суждения не могут быть одновременно истинными, но могут быть одновременно ложными. «Все бизнесмены корыстолюбивы» – ложь, а суждение «Ни один бизнесмен не является корыстолюбивым» нельзя признать истинным, оно вполне может быть и ложным. – Ложность одного из суждений оставляет другое суждение неопределенным.

Отношение между суждениями I и О называют отношением частичного совмещения (субконтрарности): суждения этого типа могут быть одновременно истинными (например, «некоторые люди искренны» – истинно и суждение типа «некоторые люди не являются искренними» также может быть истинным, но не могут быть одновременно ложными (например, если суждение «Некоторые люди не имеют сердца «– ложное, то суждение «некоторые люди имеют сердце» будет обязательно истинным). Если одно суждение ложно, то второе – обязательно истинно.

Наиболее интересным является отношение, существующее между суждениями А-О и Е- I – это отношение противоречия (контрадикторности): противоречащие суждения не могут быть одновременно истинными, но не могут быть одновременно и ложными: если одно из них истинно, то другое обязательно ложно; если одно из них ложно, то другое – обязательно истинно(например, «Все люди злы» – ложно, а суждение «некоторые люди не являются злыми» –истинно; а если суждение «Ни один кит не дышит жабрами» - истинно, то суждение «некоторые киты дышат жабрами» – ложное).

Можно обратить внимание на сходство отношений между понятиями и суждениями:

1. Противоположные понятия не исчерпывают всего объема родового понятия, в нем еще остается промежуток; точно также противоположные суждения оба могут быть ложными, и истина лежит где-то посредине.

2. Противоречащие понятия полностью разделяют объем родового понятия на две части, точно так же противоречащие суждения не оставляют места чему-то третьему: истина заключена в одном из них.

В спорах и дискуссиях могут высказываться противоречащие и противоположные суждения. Часто сложно выяснить, какие из них истинное, какое – ложное. Поэтому в процессе спора общему тезису оппонента разумнее противопоставлять противоречащее частное суждение (и – л; л – и), а не противоположное общее, где оба суждения могут оказаться ложными.

3. Третья задача «логического квадрата» состоит в том, что, если мы не знаем, каким – истинным или ложным – является исходное суждение, то по «логическому квадрату» методом «от противного» это можно определить.

Отношения между простыми суждениями можно рассмотреть в виде следующих таблиц:

Таблица № 1 «По истинности»:

	А	Е	I	O
A истинно		Ложно	Истинно	Ложно
E истинно	ложно		Ложно	Истинно
I истинно	Неопредел.	Ложно		Неопредел.
O истинно	ложно	Неопредел.	Неопредел.

Таблица № 2 «По ложности»:

	А	Е	I	O
A - ложно		Неопредел.	Неопредел.	Истинно
E - ложно	Неопредел.		Истинно	Неопредел.
I - ложно	Ложно	Истинно		Истинно
O - ложно	Истинно	Ложно	Истинно

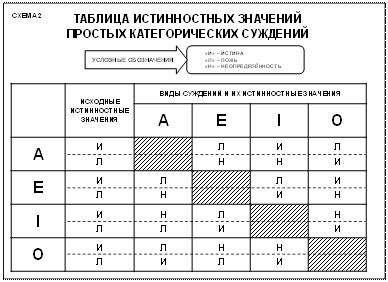Отразим в сводной таблице результаты истинности (и) и ложности (л), а также неопределённости (н) суждений А, Е, I, О.

Для использования логического квадрата необходимо руководствоваться следующими правилами.

1. Выяснить виды простых суждений, участвующих в отношениях.

2. Расположить их на логическом квадрате.

3. Обладая информацией только об одном из суждений и зная правила логического квадрата, можно вычислить значение остальных трёх.

4. Из истинности частного нельзя выводить истинность общего.

5. При опровержении общего ложного суждения нельзя прибегать к противоположному ему общему суждению, так как оно может быть ложным. Достаточно привести противоречащее ему суждение.

6. Для доказательства ложности общего суждения достаточно доказать ложность подчинённого ему частного суждения.

Сложные суждения.

Мы уже отмечали, что сложными называются суждения, образованные из двух или более простых суждений, соединенных логическими связками. Логические связки представляют собой формальные аналоги союзов нашего языка. Как сложные предложения строятся из простых с помощью союзов «однако», «или» и т.п., так и сложные суждения образуются из простых с помощью логических связок: конъюнкции, дизъюнкции, импликации, эквиваленции и отрицания.

Рассмотрим основные виды сложных суждений.

Соединительные суждения представляют собой связку двух или более простых суждений с помощью логического союза «конъюнкции». Например, «на улице холодно (а) и идет дождь(в)»: (а Ù в).

Разделительное суждение – это связь двух или более простых суждений с помощью логических связок «слабой и сильной дизъюнкции». При «слабой дизъюнкции» союз «или» рассматривается как соединительно-разделительный союз и выраженные в суждении признаки не исключают друг друга, а могут одновременно принадлежать одному и тому же предмету. Например, «Я пойду в булочную за белым (а) или черным (в) хлебом» (а Ú в). При сильной или строгой дизъюнкции союз «или (либо)» употребляется как разделительный. Выраженные признаки в сильной дизъюнкции исключают друг друга. Например, «Я поеду на юг на поезде (а) или полечу на самолете(в)» (а Ú в).

Условные (импликативные) суждения – это суждения, образованные из двух простых суждений, выражающих причинно-следственную связь явлений. Первое предложение (антецедент или основание) фиксирует причину, второе (консеквент или следствие) – следствие этой причины. Например, «Если Солнце взошло (а), то на улице стало светло (в)» (а ® в).

Для более строгого определения условного суждения следует охарактеризовать необходимые и достаточные условия. Условие называется необходимым для данного события, если при его отсутствии это событие не наступает. Например, наличие атмосферы на Земле является необходимым условием для возникновения на Земле разных видов высокоорганизованных животных, то есть без атмосферы жизнь на Земле не могла бы возникнуть. Условие называется достаточным для данного события, если всякий раз, когда имеется это условие, событие происходит. Например, выпадение дождя является достаточным условием для того, чтобы крыши домов были мокрыми.

Условия могут быть достаточными, но не необходимыми; необходимыми, но не достаточными; необходимыми и достаточными. Условным называется суждение, в котором ситуация, описываемая основанием, является достаточным условием для ситуации, описываемой следствием.

Эквивалентное суждение - это суждение, образованное из двух простых суждений с помощью логического союза «если, и только если…, то». Например, «Если и только если Солнце находится в зените (а), то тени от него являются самыми короткими (в)» (а º в). Может рассматриваться как условное суждение, если событие, описываемое основанием, является достаточным и необходимым условием для события, описываемого следствием.

Отрицательное суждение – это суждение, в котором утверждается отсутствие некоторой ситуации. Оно чаще всего выражается предложением, начинающимся словосочетанием «неверно, что» или «не». Например, «Неверно, что идет снег» (Øa).

От того, при помощи какого союза связываются простые суждения, зависит логическая особенность сложного суждения. При анализе сложного суждения можно полностью отвлекаться от внутренней структуры исходных суждений. Представление высказываний естественного языка в символическом виде с помощью символов, о которых мы уже говорили в первой лекции, означает формализацию высказывания, которая во многих случаях оказывается полезной.

Сложные суждения – это тоже мысль, которая что-то утверждает или отрицает и которая, поэтому, оказывается истинной или ложной. Вопрос об истинности простых суждений лежит вне сферы логики – на него отвечают конкретные науки, повседневная практика или наблюдение. Истинно или ложно суждение «Киты – млекопитающие»? Нужно спросить биолога и он скажет нам, что это суждение истинно. Вопрос об истинности простых суждений решается обращением к реальности, к которой относится наше суждение.

Но как установить истинность или ложность сложного суждения? Этот вопрос решает логика. Мы договариваемся или принимаем соглашения относительно того, когда высказывания с той или иной логической связкой будем считать истинными, а когда – ложными.

Соглашения, о которых идет речь, выражаются таблицами истинности для логических связок, показывающими, в каких случаях высказывание с той или иной связкой истинно, а в каких случаях мы будем считать его ложным. При этом мы опираемся на истинность или ложность простых суждений, являющихся частыми сложного суждения. «Истина» («и») и «ложь» («л») называются «истинностными значениями» суждения – если переменная представляет истинное суждение, она принимает значение «истина»; если же представляет ложное суждение, она принимает значение «ложь». Каждая переменная может представлять как истину, так и ложь.

Отрицание применяется к одному суждению. Это суждение может быть истинным или ложным.

А	Øa
И	Л
Л	И

Если исходное суждение истинно, то его отрицание ложно; если же исходное суждение ложно, то его отрицание истинно. Так, если суждение «Афины находятся в Греции» – истинно, то его отрицание «Неверно, что Афины находятся в Греции» – ложно.

Приведем таблицу истинности для остальных логических связок:

	А	в	a&в	аÚв	аÚв	а®в	аºв
1.	И	и	И	и	л	т	И
2.	И	л	Л	и	и	л	л
3.	Л	и	Л	и	т	и	л
4.	Л	л	Л	л	л	и	и

Конъюнкция истинна только в одном случае – когда оба ее члена истинны. Во всех остальных случаях – она ложна. Смысл конъюнкция – одновременность.

Слабая дизъюнкция истинна во всех случаях, кроме одного – когда оба ее члена ложны. Смысл слабой дизъюнкции – многовариантность.

Сильная (строгая) дизъюнкция истинна, когда один ее член истинен, а другой – ложен и наоборот; ложна, когда обо ее члена истинны или оба ложны. Смысл сильной дизъюнкции – альтернатива.

Эквиваленция истинна, когда ее члены имеют одно и то же значение – либо оба истинны, либо оба ложны. Смысл эквиваленции – взаимозаменяемость.

Сложнее обстоит дело с импликацией. Импликация выражает соотношение причины и следствия таким образом, что причина «а» является достаточным основанием для того, чтобы наступило следствие «в». Импликация истинна во всех случаях, кроме одного – когда из истинного основания пытаются сделать ложное следствие. Кроме того, в формальной логике действует принцип: из лжи следует всё, что угодно, в том числе и истина. Однажды Бертрана Рассела попросили: если ложное допущение позволяет доказывать всё, что угодно, то покажите, что из ложного суждения 5=4 следует, что «Вы – римский папа». Б.Рассел ответил: «Это не трудно! Из 5=4 следует, что 2=1. Папа и я образуем двойку, стало быть – мы – одно и то же». Конечно, ответ Рассела был шуткой. «Всё, что угодно» должно быть ограничено языком той теории, в которой появляется противоречие, в данном случае – арифметикой. Рассуждения же о римском папе к ней (арифметике) не относится. Однако слова Рассела хорошо передают суть дела – в противоречивой системе утрачивается различие между истиной и ложью, следовательно, она ничего не может описать.

«На вопрос, кто из трех студентов изучал логику, был получен ответ:»Если изучал первый, то изучал и второй, но неверно, что, если изучал третий, то изучал и второй». Кто же в действительности изучал логику, если известно, что полученный ответ является истинным?

1-ый изучал логику обозначим за «а», 2-ой изучал логику – за «в», 3-ий изучал логику – «с». В результате получим следующую запись задачи: (а → в)^¬(с→ в). Составим таблицу этого сложного суждения:

а в с: (а → в)^¬(с→ в).

и и и и л л и

и и л и л л и

и л и л л и л

и л л л л л и

л и и и л л и

л и л и л л и

л л и и и и л

л л л и л л и

По результатам этой таблицы ясно видно, что логику изучал лишь третий студент.

В некоторых случаях простые и сложные суждения выражаются в предложениях, начинающихся со слов «Неверно, что» или «Не». Это значит, что отрицается суждение, которое стоит после таких слов. Для прояснения смысла суждений, их следует преобразовать в эквивалентные суждения, перед которыми отрицание не стоит, то есть преобразовать в суждения, где нет внешнего отрицания. Иногда, наоборот, требуется провести отрицание суждения.

1. Провести отрицание простых категорических суждений:

ØAºO; ØEºI; ØOºA; ØIºE.

Можно посмотреть по «логическому квадрату»: отрицание простого категорического суждения эквивалентно его противоречию, противоречивому суждению.

Например, «неверно, что некоторые студенты могут не сдавать экзамены» – это частноотрицательное суждение, его отрицание эквивалентно общеутвердительному суждению «Все студенты должны сдавать экзамены».

2. Отрицание единично-отрицательного суждения эквивалентно единично-утвердительному и наоборот. «Не было дня в этом месяце, когда бы не шел дождь» эквивалентно суждению «Каждый день в этом месяце шел дождь».

3. Отрицание сложных суждений производится согласно следующих формул эквивалентности:

1) Ø(AÙB)ºØAÚØB Отрицание конъюнкции эквивалентно

дизъюнкции отрицаний.«Неверно, что

шел дождь и светило солнце».º «Или не

шел дождь или не светило солнце».

2) Ø(AÚB)ºØAÙØB. Отрицание дизъюнкции эквивалентно

конъюнкции отрицаний. «Неверно, что

он или больной или уехал в

командировку». º «Он не больной и не

уехал в командировку».

3) Ø(A®B)ºAÙØB. Отрицание импликации эквивалентно

конъюнкции первого члена и отрицания

второго члена. «Неверно, что если

деревянный брус нагреть до 100

градусов, то он обуглиться» º

«Деревянный брус нагрели до 100

градусов, но он не обуглился».

4) Ø(AºB)º(ØAÙB)Ú(AÙØB). Отрицание эквиваленции

эквивалентно дизъюнкции двух конъюнкций «Неверно, что человек не может

работать тогда и только тогда, когда

он больной» º «Или человек

может работать, хотя он и

больной, или он не может работать,

хотя и не больной».

5)ØØAºA. Двойное отрицание некоторого высказывания

эквивалентно самому этому высказыванию. «Неверно,

что он не прав» º «Он прав».

5) Ø(AỲB)º(AΛB)ν (¬А Λ¬В). Отрицание сильной дизъюнкции эквивалентно дизъюнкции двух

конъюнкций. Либо, в некоторых работах рассмотрено, что отрицание сильной дизъюнкции эквивалентно эквиваленции этих суждений ¬(AÝB)≡(А≡В)

«Неверно, что на встречу пойдет либо он,

либо другой» º «На встречу пойдет и он и

другой или на встречу не пойдет ни он, ни

другой» либо: «Он пойдет на встречу тогда

и только тогда, когда на нее пойдет другой».

Покажем, как эти отношения эквивалентности между высказываниями могут быть использованы для решения логических задач.

Например, в деле об убийстве имеется двое подозреваемых: Пьер и Жан. Допросили четырех свидетелей. Показание первого свидетеля таково: «Я знаю только, что Пьер не виноват». Второй свидетель сказал: «Я знаю лишь, что Жан не виноват». Третий свидетель: «Я знаю, что из первых двух показаний по меньшей мере одно истинно». Четвертый: «Я знаю, что показания третьего свидетеля ложны». Четвертый свидетель оказался прав. Кто же совершил преступление?

Логика существенно облегчает процесс размышления. Обозначим высказывание «Пьер виноват» через «а»; высказывание «Жан виноват» через «в». Тогда показание первого свидетеля будет «Øa»; показание второго свидетеля «Ø в»; третий свидетель утверждает дизъюнкцию показаний двух свидетелей, то есть «ØaÚØ в»; четвертый свидетель утверждает, что эта дизъюнкция ложна, то есть отрицает ее: «Ø(ØaÚØв). Нам сказано, что последнее утверждение истинно. Теперь преобразуем его, опираясь на эквивалентности

Ø(ØaÚØ в) ºØØaÙØØ в º aÙ в. Эта конъюнкция истинна, а это значит, что Пьер и Жан вместе совершили преступление.

Отношения между сложными суждениями.

В различных отношениях находятся не только простые, но и сложные суждения. Сложные суждения считаются сравнимыми лишь в том случае, если в их составе есть хотя бы одно общее простое суждение.

Сравнимые суждения делятся на совместимые и несовместимые. Суждения называются совместимыми, если они могут быть одновременно истинными.

Совместимость бывает трех видов:

1. суждения эквивалентны, если всегда принимают одинаковые истинностные значения;

2. суждения частично совместимы, если невозможна их совместная ложность.

3. Суждение находится в отношении подчинения (логического следования) к другому, если при этом подчиненное суждение обязательно истинно во всех случаях, когда истинно подчиняющее (или сформулируем иначе: если не может быть такой ситуации, когда первое суждение было истинно, а второе – ложно).

Суждения называются несовместимыми, если не могут быть одновременно истинными.

Несовместимость бывает двух видов:

1. противоречие суждений имеет место тогда, когда эти суждения не могут принимать одинаковые значения – ни истинные, ни ложные.

2. Противоположность имеет место, когда суждения не могут быть одновременно истинными, но могут быть одновременно ложными.

Сравнимые суждения иногда бывают независимыми, иначе говоря, могут иметь все четыре сочетания своих истинностных значений: ии, ил, ли, лл.

Выводы

Суждение – это форма мысли, в которой что-либо утверждается или отрицается о предмете мысли.

Основной логической характеристикой суждений является истинностное значение, вокруг которого и разворачивается логический анализ высказываний.

Суждения бывают простыми и сложными. Простые суждения в зависимости от того, что утверждается или отрицается в них, делятся на атрибутивные, реляционные и экзистенциальные.

Основные характеристики атрибутивных (простых категорических) суждений – это количество и качество, на основе которых и осуществляется классификация данных суждений.

В объединённой классификации атрибутивных суждений, сочетающей количественные и качественные характеристики, выделяют: общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные суждения.

Специфическими видами атрибутивных высказываний являются выделяющие и исключающие суждения.

Логическая природа атрибутивных суждений раскрывается не только посредством содержательного анализа терминов, но и установления объёмных соотношений между ними.

Анализ объёмных соотношений терминов позволяет установить их количественные характеристики (распределённость) и тем самым уточнить предметное поле высказывания.

Существуют правила распределённости терминов, по которым субъекты распределены в общих суждениях и не распределены в частных, а предикаты распределены в отрицательных и не распределены в утвердительных суждениях. В выделяющих суждениях предикаты всегда распределены.

Сложные суждения образуются из простых с помощью логических союзов. В зависимости от функций логических союзов выделяют следующие виды сложных высказываний: соединительные (конъюнкция), разделительные (дизъюнкция), условные (импликация), равносильные (эквиваленция), суждения с внешним отрицанием и комбинированные.

Истинностное значение сложных суждений зависит от истинности или ложности входящих в их состав простых суждений и от функций логических союзов.

Установление истинностных значений сложных высказываний осуществляется с помощью таблиц истинности.

Суждения бывают сравнимыми и несравнимыми. У сравнимых суждений есть хотя бы частично общее содержание, у несравнимых – нет. Логические отношения возможны только между сравнимыми понятиями.

Сравнимость простых суждений обеспечивается наличием у них одинаковых терминов (включая и их отрицания, а также перемену логических функций).

Сравнимость сложных суждений обеспечена наличием в их составе хотя бы одного общего простого высказывания.

Главная цель логического анализа отношений между суждениями – установление истинностных значений одних высказываний на основе достоверной информации об истинности или ложности других.

Основные типы отношений между суждениями это: совместимость по истинности, совместимость по ложности и отношения логического следования.

Различные сочетания этих характеристик формируют следующие виды логических отношений: равнозначность, противоположность, противоречие, подчинение и подпротивоположность.

У простых категорических суждений эти виды отношений легко устанавливаются по логическому квадрату. Для сложных суждений необходимо составление таблиц истинностных значений.

На основе отношений противоречия выполняется логическая операция отрицания суждений, обеспечивающая однозначную оценку истинности или ложности высказывание.

Система ферментов и белков, обеспечивающая взаимосвязь (сопряжение) процессов окисления и фосфорилирования АДФ, получила название цепи переноса электронов (ЦПЭ) или дыхательной цепи.

В основе ЦПЭ лежит работа 3-х важнейших ферментативных комплексов.

· Первый ферментативный комплекс NADН-дегидрогеназа (I) представляет собой белок, имеющий простетическую группу – FMN, коферментом является рибофлавин (витамин В₂). NADН-дегидрогеназа катализирует перенос 2Н с кофермента NADН на FMN, который переходит в форму FMNН₂. Второй протон поглощается из матрикса. Реакция протекает по уравнению:

NADH + Н⁺ + Е (FMN) → NAD⁺ + Е (FMNH₂)

С FMNH₂ электроны переносятся затем на ряд железо-серных белков (FeS), играющих роль второй простетической группы в молекуле NADH-дегидрогеназы.

Атомы железа в таких белках могут принимать и отдавать электроны поочерёдно, переходя в ферро- (Fe₂₊) и ферри- (Fe₃₊) состояния. Затем электроны переносятся на кофермент Q (убихинон).

· Убихинон (кофермент Q₁₀) – жирорастворимое витаминоподобное вещество, широко распространённое в клетках всех организмах. Молекулы убихинона в зависимости от источника, из которого они выделены, различаются длиной углеводородной цепи, которая у млекопитающих содержит 10 изопреноидных звеньев и обозначается как Q₁₀. Убихинон способен восстанавливаться и превращаться в убихинол, имеющий 2 ОН-группы.

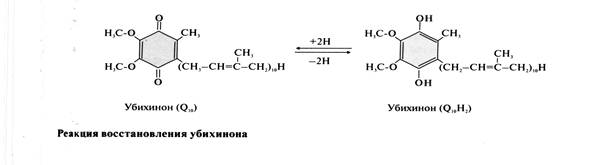
В реакции восстановления убихинон принимает от FMNН₂ 2е, таким образом в результате работы NADH-дегидрогеназы кофермент NADH переходит в окисленную форму.

NADH + Н⁺ + Q → NAD⁺+ QH₂.

· Ферментный комплекс QH₂-дегидрогеназа (IIi) представляет сложный белок, включающий цитохромы (b₁ и b₂) и цитохром с₁. В ЦПЭ участвуют 5 типов цитохромов (а, а₃, b, с, с₁). За исключением цитохрома с, все цитохромы находятся во внутренней мембране митохондрий в виде сложных белковых комплексов. Рабочей частью всех цитохромов является гемм, содержащий ион Fe²⁺, который может принимать электрон и менять валентность.

QН₂-дегидрогеназа переносит электроны от убихинола на цитохром с. Внутри комплекса III электроны передаются от цитохромов b на FeS-центры, на цитохром с₁, а затем на цитохром с. Группы гема, подобно FeS-центрам, переносят только по одному электрону. Таким образом, от молекулы QH₂ 2 электрона переносятся на 2 молекулы цитохрома b.

· Цитохромоксидаза (ферментный комплекс IV) состоит из 2 цитохромов а и а₃, а также ионы меди, которые могут изменять свою валентность и участвуют в переносе электронов на кислород.

Cu⁺ ↔ Cu²⁺ + e,
Fe²⁺ ↔ Fe³⁺ + e.

Цитохромы а и а₃ в восстановленной форме имеют высокое сродство к кислороду, который принимает два электрона и переходит в ионизированную форму. В активном центре цитохромоксидазы кислород присоединяет 2Н⁺ из матрикса и образуется молекула воды.

Работа комплекса IV цитохромоксидазы также сопровождается переносом Н⁺ из матрикса в межмембранное пространство (против градиента концентрации).

Таким образом, все ферментативные комплексы ЦПЭ, участвующие в передаче электронов, обеспечивают перекачивание Н⁺ из матрикса в межмембранное пространство.

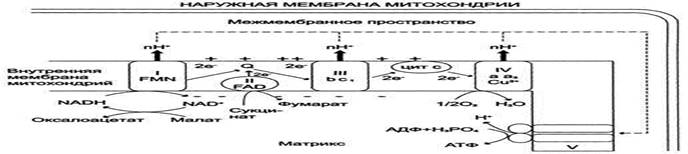
I - NADH-дегидрогеназа; II - сукцинат дегидрогеназа; III - QН₂-дегидрогеназа; IV - цитохромоксидаза; V - АТФ-синтаза.

Повышение концентрации Н⁺ в межмембранном пространстве приводит к возникновению градиента электрохимического потенциала ΔμН⁺. Энергия ΔμН⁺ используется для синтеза АТФ, если протоны возвращаются в матрикс через ионные каналы АТФ-синтазы.

Порядок участия ферментов в работе цепи обусловлен величиной их окислительно-восстановительного потенциала, который возрастает от одного компонента к другому.

Компонент ЦПЭ	окислительно-восстановительный потенциал, Е0
NAD^+/ NADH	-0,32
FMN//FMNH2	-0,22
Q/QH2	+0,10
Цитохром с	+0,25
О2/Н2О	+0,82

Работу ЦПЭ объясняет хемиосмотическая теория Митчелла, основные положения которой объясняют механизмы сопряжения процессов биологического окисления и фосфорилирования АДФ.

При движении от окисляемого субстрата к кислороду электроны теряют часть своей энергии. Эту энергию ферменты ЦПЭ используют для переноса протонов из матрикса в межмембранное пространство против градиента концентрации, т.е. комплексы ЦПЭ работают как протонный насос, перекачивая Н⁺.

Градиент электрохимического потенциала стимулирует возвращение протонов из межмембранного пространства в матрикс. Но внутренняя мембрана митохондрий для Н⁺ непроницаема. Их перенос происходит с помощью фермента АТФ-синтазы (комплекс V), имеющего протонный канал F₀. Н⁺ межмембранного пространства присоединяются к ферменту, изменяя его заряд и конформацию. Это приводит к раскрытию протонного канала, переносу Н⁺ в матрикс по градиенту концентрации и активации поверхностной части фермента, катализирующей реакцию образования АТФ.

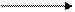АДФ + Н₃РО₄ АТФ + Н₂О

Образующиеся молекулы АТФ траспортируются из матрикса в цитозоль АДФ-АТФ-транслоказами, которые одновременно переносят АДФ в митохондрию.

Количество АТФ, образующееся в результате сопряжения работы ЦПЭ и АТФ-синтазы, оценивается с помощью к оэффициент окислительного фосфорилирования.

Окисление молекулы NADH в ЦПЭ сопровождается образованием 3 молекул АТФ; энергия электронов и протонов в ЦПЭ от FAD-зависимых дегидрогеназ (сукцинатдегидрогеназа), достаточна для активации АТФ-синтазы и фосфорилирования 2 молекул АТФ. Отношение количества фосфорной кислоты (Р), использованной на фосфорилирование АДФ, к атому кислорода (О), поглощённого в процессе дыхания, называют коэффициентом окислительного фосфорилирования и обозначают Р/О. Следовательно, для NADH Р/О = 3, для сукцината Р/О - 2.

Для синтеза АТФ используется не вся энергия, выделяющаяся в процессе переноса электронов и протонов в ЦПЭ, а примерно 40-50%. Более 30% всей энергии выделяется в виде тепла, обеспечивая поддержание температуры тела человека. Остальная энергия используется для работы клеток (например, для транспорта веществ через мембрану).

Биологические функции ЦПЭ

· Использует энергию окисления субстратов для синтеза АТФ путем окислительного фосфорилирования

· Обеспечивает поддержание температуры тела

В норме скорость окисления первичных доноров Н⁺ и электронов регулируется содержанием АДФ. Выполнение клеткой работы с затратой АТФ приводит к накоплению АДФ, это активирует окисление субстратов и поглощение кислорода митохондриями клетки.

Таким образом, клетки реагируют интенсивность метаболизма и поддерживают соотношение АТФ/АДФ на необходимом уровне. Зависимость интенсивности поглощения кислорода от концентрации АДФ называется дыхательным контролем.

Механизм дыхательного контроля характеризуется высокой точностью и имеет важное значение, так как в результате его действия скорость синтеза АТФ соответствует потребностям клетки в энергии. Запасов АТФ в клетке не существует. Относительные концентрации АТФ/АДФ в тканях изменяются в узких пределах, в то время как потребление энергии клеткой, т.е. частота оборотов цикла АТФ и АДФ, может меняться в десятки раз.

Транспорт АТФ и АДФ через мембраны митохондрий

В большинстве эукариотических клеток синтез АТФ происходит внутри митохондрии, а основные потребители АТФ расположены вне её. С другой стороны, в матриксе митохондрий должна поддерживаться достаточная концентрация АДФ. Эти заряженные молекулы не могут самостоятельно пройти через липидный слой мембран. Внутренняя мембрана непроницаема для заряженных и гидрофильных веществ, но в ней содержится определённое количество транспортёров, избирательно переносящих подобные молекулы из цитозоля в матрикс и из матрикса в цитозоль.

В мембране есть белок АТФ/АДФ-антипортер, осуществляющий перенос этих метаболитов через мембрану.

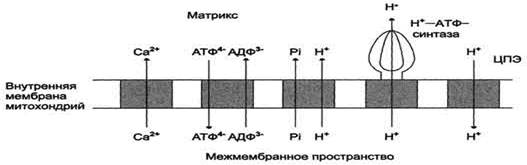
Потоки различных веществ (АТФ, АДФ, Н₃РО₄, Са²⁺) проходят через специфические транспортёры, при этом затрачивается энергия электрохимического потенциала мембраны.

Молекула АДФ поступает в митохондриальный матрикс только при условии выхода молекулы АТФ из матрикса.

Движущая сила такого обмена - мембранный потенциал переноса электронов по ЦПЭ. Расчёты показывают, что на транспорт АТФ и АДФ расходуется около четверти свободной энергии протонного потенциала. Другие транспортёры тоже могут использовать энергию электрохимического градиента. Так переносится внутрь митохондрии неорганический фосфат, необходимый для синтеза АТФ. Непосредственным источником свободной энергии для транспорта Са²⁺ в матрикс также служит протонный потенциал, а не энергия АТФ.

Дата добавления: 2014-01-05