
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Условия единственности решения уравнений электродинамики
|
|
|
|
Тема 5.
1. Вводные замечания
Уравнения Максвелла являются дифференциальными уравнениями в частных производных. Такие уравнения допускают множество решений. Однако из общих физических представлений очевидно, что при полном повторении условий эксперимента распределение поля должно быть одинаковым. Следовательно, в каждом конкретном случае электромагнитное поле должно удовлетворять не только уравнениям Максвелла, но и некоторым дополнительным условиям. Эти дополнительные условия определяются специальными теоремами, называемыми теоремами единственности решения задач электродинамики. Рассмотрим доказательство теорем для краевых задач в случае монохроматического поля, и считаем, что в рассматриваемой части пространства происходит поглощение энергии, т.е. что  .
.
2. Единственность решения внутренних задач электродинамики
 Покажем, что внутренняя задача электродинамики имеет единственное решение, если на граничной поверхности
Покажем, что внутренняя задача электродинамики имеет единственное решение, если на граничной поверхности  (см. рис8) выполняется одно из следующих четырех условий:
(см. рис8) выполняется одно из следующих четырех условий:
 а) в каждой точке М поверхности
а) в каждой точке М поверхности  задана проекция вектора
задана проекция вектора  на плоскость
на плоскость 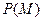 , касательную к
, касательную к  в точке
в точке 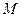 (Е-задача):
(Е-задача):
 (1)
(1)
б) в каждой точке 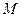 поверхности
поверхности  задана проекция вектора
задана проекция вектора  на плоскость
на плоскость 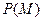 (
( -задача):
-задача):
 (2)
(2)
в) на одной части поверхности  (обозначим ее
(обозначим ее  ) задана проекция
) задана проекция 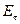 вектора
вектора  , а на другой части (
, а на другой части (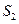 ) - проекция
) - проекция  вектора
вектора 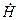 на плоскость
на плоскость 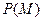 , причем
, причем  (
( -задача):
-задача):
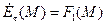 при
при 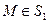 и
и  при
при 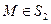 (3)
(3)
в каждой точке 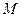 поверхности
поверхности  проекции векторов
проекции векторов  и
и 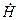 на плоскость
на плоскость 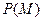 связаны соотношением
связаны соотношением
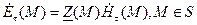 (4)
(4)
причем
 (5)
(5)
Условие (4) называют импедансным краевым условием. Очевидно, что векторы Ёт и Нт., образующиеся при проецировании  и
и 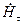 на плоскость
на плоскость 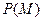 , имеют различное направление:
, имеют различное направление: 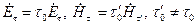 , где
, где 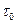 и
и 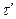 -единичные векторы, лежащие в плоскости
-единичные векторы, лежащие в плоскости 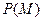 .
.
В формулах (1)-(5) через  и
и  обозначены известные (заданные) функции точки
обозначены известные (заданные) функции точки  .
.
Предположим, что существуют два различных решения поставленной задачи  и
и 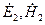 и рассмотрим их разность:
и рассмотрим их разность:
 ,
, 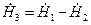 (6)
(6)
Векторы  и
и 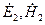 удовлетворяют уравнениям Максвелла
удовлетворяют уравнениям Максвелла
 (7)
(7)
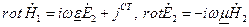 (8)
(8)
(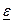 и
и  -комплексные диэлектрическая и магнитная проницаемости соответственно)
-комплексные диэлектрическая и магнитная проницаемости соответственно)
и одинаковым краевым условиям на поверхности S. Уравнения Максвелла для поля  получаются почленным вычитанием уравнения (8) из (7). При этом векторы
получаются почленным вычитанием уравнения (8) из (7). При этом векторы  сокращаются, и уравнения Максвелла для поля Ё3, Н3 принимают вид
сокращаются, и уравнения Максвелла для поля Ё3, Н3 принимают вид
 (9)
(9)
На поверхности  поле
поле  должно удовлетворять следующим краевым условиям: в случае
должно удовлетворять следующим краевым условиям: в случае  -задачи
-задачи
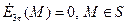 ; (10)
; (10)
в случае  -задачи
-задачи
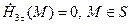 (11)
(11)
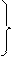 в случае
в случае  -задачи
-задачи
 (12)
(12)
 ;
;
в случае импедансного краевого условия (4)
 (13)
(13)
Составим уравнение баланса для средней за период мощности разностного поля  . Так как векторы
. Так как векторы  удовлетворяют уравнениям Максвелла (9), то мощность сторонних источников разностного поля
удовлетворяют уравнениям Максвелла (9), то мощность сторонних источников разностного поля 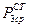 равна нулю, тогда
равна нулю, тогда
 (14)
(14)
Так как  , где
, где 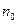 -орт внешней нормали к поверхности
-орт внешней нормали к поверхности  , то произведение
, то произведение 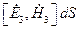 определяется только касательными составляющими векторов
определяется только касательными составляющими векторов 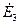 и
и 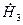 . В случае выполнения условий (2.10)-(2.12) произведение
. В случае выполнения условий (2.10)-(2.12) произведение 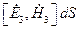 на поверхности
на поверхности  обращается в нуль. При этом из (2.14) следует, что
обращается в нуль. При этом из (2.14) следует, что
 (15)
(15)
Предположим вначале, что потери энергии в объеме 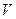 обусловлены только наличием проводимости (
обусловлены только наличием проводимости (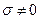 ), т.е. что
), т.е. что  , а
, а 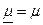 . В этом случае уравнение (15) принимает вид
. В этом случае уравнение (15) принимает вид
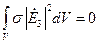 (16)
(16)
Так как 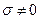 , а
, а 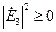 , то из равенства (16) следует, что
, то из равенства (16) следует, что  . Используя второе уравнение Максвелла, записанное относительно векторов
. Используя второе уравнение Максвелла, записанное относительно векторов 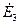 и
и 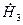 , получаем
, получаем 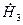 =0. Следовательно,
=0. Следовательно, 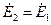 , и
, и 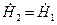 , т.е. задача имеет единственное решение.
, т.е. задача имеет единственное решение.
Рассмотрим теперь краевое условие (4).

В этом случае подынтегральное выражение во втором слагаемом в уравнении (14) может быть преобразовано следующим образом: 
При этом из (14) получаем соотношение
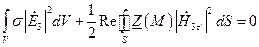 (17)
(17)
Так как 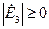 ,
,  и, кроме того, выполняется условие (5), то равенство (17) возможно только при
и, кроме того, выполняется условие (5), то равенство (17) возможно только при 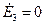 . Таким образом, и в этом случае задача имеет единственное решение.
. Таким образом, и в этом случае задача имеет единственное решение.
Единственность решения в более общем случае, когда  и
и 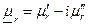 , доказывается аналогично на основе анализа уравнения (14).
, доказывается аналогично на основе анализа уравнения (14).
3. Единственность решения внешних задач электродинамики
В случае внешней задачи электродинамики поверхность S не охватывает рассматриваемую часть пространства, простирающуюся до бесконечности. Поэтому для единственности решения кроме одного из условий (1)—(4) требуется задать дополнительное условие, характеризующее поведение векторов  и
и  в точках, бесконечно удаленных от поверхности
в точках, бесконечно удаленных от поверхности  . Выясним, каким должно быть это дополнительное условие.
. Выясним, каким должно быть это дополнительное условие.
Пусть на  выполняется одно из условий (1)-(4). Предположим, что имеется два решения задачи
выполняется одно из условий (1)-(4). Предположим, что имеется два решения задачи  ,
, 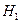 , и
, и  ,
, 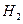 , и введем в рассмотрение разностное поле
, и введем в рассмотрение разностное поле 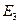 ,
,  по формулам (2.6). Как и в случае внутренней задачи электродинамики, векторы
по формулам (2.6). Как и в случае внутренней задачи электродинамики, векторы 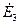 и
и 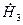 удовлетворяют уравнениям Максвелла (9) и одному из условий (10)—(13) на поверхности
удовлетворяют уравнениям Максвелла (9) и одному из условий (10)—(13) на поверхности  . Из произвольной точки 0 внутри области
. Из произвольной точки 0 внутри области 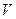 мысленно проведем сферу радиуса
мысленно проведем сферу радиуса 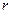 так, чтобы вся область
так, чтобы вся область 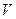 и все сторонние источники оказались внутри этой сферы. Объем, заключенный между поверхностями
и все сторонние источники оказались внутри этой сферы. Объем, заключенный между поверхностями  и
и  , обозначим через
, обозначим через 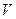 (рис.8). Составим уравнение баланса для средних за период значений мощности поля
(рис.8). Составим уравнение баланса для средних за период значений мощности поля 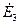 ,
, 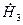 в объеме
в объеме 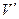 :
:
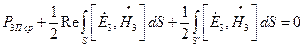 (18)
(18)
Перейдем в уравнении (18) к пределу при 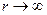 . Тогда область
. Тогда область 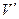 распространится на все пространство, внешнее по отношению к области
распространится на все пространство, внешнее по отношению к области 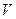 . Если в пределе третье слагаемое в левой части уравнения (18) окажется равным нулю, то получающееся при этом соотношение
. Если в пределе третье слагаемое в левой части уравнения (18) окажется равным нулю, то получающееся при этом соотношение
 (19)
(19)
не будет иметь принципиальных отличий от аналогичного уравнения (14) для внутренней задачи электродинамики, и, следовательно, рассматриваемая задача также будет иметь единственное решение. Действительно, при выполнении условий (1)—(3), второе слагаемое в левой части (19) обращается в нуль, и это уравнение принимает вид
 (20)
(20)
В частном случае, когда потери в среде обусловлены только наличием проводимости, т.е. когда  и
и 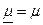 , уравнение (20) записывается в форме
, уравнение (20) записывается в форме
 (21)
(21)
Так как 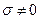 и
и 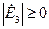 , то из (21) получаем
, то из (21) получаем 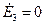 , а из второго уравнения Максвелла -
, а из второго уравнения Максвелла - 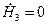 . Следовательно,
. Следовательно, 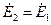 и
и 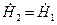
Если на поверхности  выполняется условие (4), то из уравнений (19) и (13) имеем
выполняется условие (4), то из уравнений (19) и (13) имеем
 ,
,
откуда также следует единственность решения.
Найдем условие, при котором
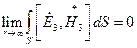 (22)
(22)
и, следовательно, проведенное выше доказательство справедливо. При 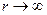 поверхность
поверхность  возрастает пропорционально
возрастает пропорционально  . Поэтому для выполнения условия (22) необходимо, чтобы абсолютная величина произведения
. Поэтому для выполнения условия (22) необходимо, чтобы абсолютная величина произведения  при
при 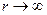 убывала быстрее
убывала быстрее  . Для этого достаточно потребовать, чтобы искомые векторы
. Для этого достаточно потребовать, чтобы искомые векторы  и
и  убывали быстрее, чем
убывали быстрее, чем  .
.
Таким образом, внешняя задача электродинамики имеет единственное решение, если на поверхности  , ограничивающей объем
, ограничивающей объем 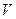 , выполняется одно из условий (1)-(4) и, кроме того, при
, выполняется одно из условий (1)-(4) и, кроме того, при 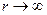 векторы
векторы  и
и  убывают быстрее, чем
убывают быстрее, чем  . Последнее всегда имеет место, так как в любых реальных средах имеются потери энергии.
. Последнее всегда имеет место, так как в любых реальных средах имеются потери энергии.
Отметим, что теорему единственности для внешней задачи электродинамики можно доказать и в случае среды без потерь, если вместо условия убывания векторов  и
и  при
при 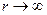 быстрее
быстрее  потребовать выполнения следующих соотношений:
потребовать выполнения следующих соотношений:
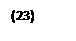


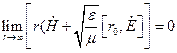
Предельные соотношения (23) называются условиями излучения. Они были сформулированы Зоммерфельдом. Физически эти условия эквивалентны требованию, чтобы при 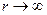 поле имело характер поперечных волн, распространяющихся вдоль направления
поле имело характер поперечных волн, распространяющихся вдоль направления 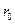 (предполагается, что источники поля находятся на конечном расстоянии от поверхности
(предполагается, что источники поля находятся на конечном расстоянии от поверхности  ). Из приведенного выше доказательства единственности решения краевых задач электродинамики следует, что при отсутствии потерь энергии в области
). Из приведенного выше доказательства единственности решения краевых задач электродинамики следует, что при отсутствии потерь энергии в области 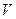 решение внутренней задачи может быть неединственным. Физически это означает, что в такой системе помимо полей, созданных непрерывно действующими сторонними источниками, могут существовать незатухающие поля, созданные когда-то действовавшими сторонними источниками (но в рассматриваемое время переставшими действовать). Эти поля из-за отсутствия потерь в среде могут существовать сколь угодно долго (например, собственные колебания идеального объемного резонатора).
решение внутренней задачи может быть неединственным. Физически это означает, что в такой системе помимо полей, созданных непрерывно действующими сторонними источниками, могут существовать незатухающие поля, созданные когда-то действовавшими сторонними источниками (но в рассматриваемое время переставшими действовать). Эти поля из-за отсутствия потерь в среде могут существовать сколь угодно долго (например, собственные колебания идеального объемного резонатора).
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 787; Нарушение авторских прав?; Мы поможем в написании вашей работы!