Табулирование функции

Вычисление производных.

Вычисление пределов.

Символьные вычисления в среде MATLAB.

Лекция № 7.

В состав MATLAB входит ToolBox Symbolic Math, предназначенный для вычислений в символьном виде. Преобразование выражений, отыскание аналитического решения задач линейной алгебры, дифференциального и интегрального исчисления, получение численного результата с любой точностью-вот далеко не полный перечень возможностей, предоставляемых данным ToolBox. Объектно-ориентированный подход, реализованный в MATLAB, позволил сделать работу с символическими выражениями простой и удобной.

Символьные переменные и функции являются объектами класс sym object, в отличии от числовых переменных, которые содержатся в массивах double array. Символьный объект создается при помощи функции syms.

Команда

>> syms x a b

создает три символьные переменные х, а, b. Размер памяти, отводимый под символьные переменные, достаточно большой.

Конструирование символических функций от переменных класса sym object производится с использованием обычных арифметических операций и обозначений для встроенных математических функций, например:

> f=(sin(x)+a)^2*(cos(x)+b)^2/sqrt(abs(a+b))

f =

(sin(x)+a)^2*(cos(x)+b)^2/abs(a+b)^(1/2)

Запись формулы для выражения в одну строку не всегда удобна, более естественный вид выражения выводит в командное окно функция pretty ():

Определенная функция f также является символической переменной типа sym object, в чем несложно убедиться при помощи команды whos:

>> whos f

Name Size Bytes Class

f 1x1 204 sym object

Grand total is 41 elements using 204 bytes

Имеющиеся символические переменные и функции позволяют образовывать новые символические выражения:

Символическую функцию можно создать без предварительного объявления переменных при помощи sym, входным аргументом которой является строка с выражением, заключенная в апострофы:

Замечание. Функция sym может быть использована для объявления символических переменных. Команда syms a,b,c эквивалентна последовательности a=sym('a');b=sym('b');c=sym('c').

Математическая функция может быть представлена в виде формулы, таблицы, графика. Табличное представление функции необходимо в следующих случаях:

· определение погрешности интерполяции;

· вычисление табличных разностей с целью определения степени интерполяционного полинома;

· определение области изоляции корня;

· оценка численных значений функции в широком диапазоне.

В среде MATLAB табулирование функции осуществляется с помощью функции subs(f,x,x1), где:

f -функция, заданная аналитически;

x - аргумент функции f;

х1 - вектор значений аргумента х, при котором определяется значение функции f.

Переменная х1 может представляться в виде вектора или при постоянном шаге в виде: , где 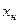-начальное значение х1, 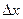- шаг, 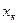-конечное значение х1.

Технология табулирования функции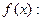

1. Определение группы символьных переменных с помощью функции syms.

2. Образование вектора х1.

3. Ввод функции табулирования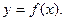

4. Образование функции табулирования subs.

5. Получение решения путем нажатия клавиши <Enter>.

Пример: найти значения функции 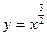для х1 в диапазоне [0;1] с постоянным шагом h = 0.01 и в случае, когда х1 =[0, 0.5, 1, 3, 5].

Решение:

>> syms x,x1,y;

>> x1=[0,0.5,1,3,5];

>> y=x.^(3/2);

>> subs(y,x,x1)

ans = 0 0.3536 1.0000 5.1962 11.1803

Функция subs позволяет табулировать одновременно несколько функций. Для этого необходимо функцию 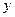представить в виде матрицы табулируемых функций, например,

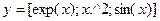
MATLAB позволяет табулировать функции, используя матричные операции и не обращаясь к функции subs. Технология вычислений в этом случае состоит в выполнении следующих операций;

1. Определение символьных переменных с помощью функции syms.

2. Образование вектора аргумента х.

3. Образование матрицы, элементами которой являются аргумент х и табулируемые функции.

4. Получение решения путем нажатия клавиши <Enter>.

5. При необходимости получение решения в столбик используется функция 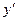(транспонирование).

Пример: найти значения функций 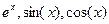в диапазоне изменения х, равном [0;1], с шагом 0,2. Решение получить в виде матрицы.

Решение:

>> syms x,y;

>> x=0:0.2:1;

>> y=[x; exp(x);sin(x);cos(x)]

y =

0 0.2000 0.4000 0.6000 0.8000 1.0000

1.0000 1.2214 1.4918 1.8221 2.2255 2.7183

0 0.1987 0.3894 0.5646 0.7174 0.8415

1.0000 0.9801 0.9211 0.8253 0.6967 0.5403

>> y'

ans =

0 1.0000 0 1.0000

0.2000 1.2214 0.1987 0.9801

0.4000 1.4918 0.3894 0.9211

0.6000 1.8221 0.5646 0.8253

0.8000 2.2255 0.7174 0.6967

1.0000 2.7183 0.8415 0.5403

Дата добавления: 2014-01-05