
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод ветвей и границ
|
|
|
|
...
 1 2 N 2 K
1 2 N 2 K
 |  | ||||||||
 |  | ||||||||
 | |||||||||
2... N 1 1 2... N 1 1 2 N 1
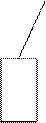
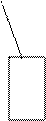
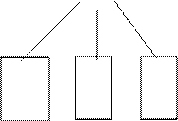
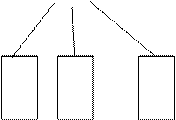
Рис. 11 Схема поиска неисправности по иерархическому принципу
Способ построения алгоритма поиска неисправностей методом ветвей и границ используется для синтеза алгоритмов поиска неисправностей в РЭА, функциональная модель, которой представляет собой произвольную структуру. Он позволяет определить наилучшую последовательность поиска среди возможных. Исходными данными являются функциональная модель ОД, таблица неисправностей с вероятностями различных состояний и стоимости контроля выходных параметров функциональных элементов. Целью данного метода является определить такую последовательность контроля параметров, которая будет обладать минимальной средней стоимостью при поиске любого неисправного элемента.
Средняя стоимость произвольной программы поиска неисправностей
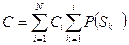 или
или 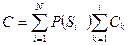 , (46)
, (46)
где Ci – стоимость контроля i – параметра;
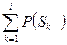 - сумма вероятностей состояний, которые рассматриваются при контроле i – параметра.
- сумма вероятностей состояний, которые рассматриваются при контроле i – параметра.
Расчет поиска начинается с любого i – параметра, который разбивает всё множество возможных состояний S на два подмножества: S0 (zi) и S1 (zi), соответствующие отрицательному и положительному результатам контроля параметра zi соответственно.
Последовательность контроля остальных параметров из приведенных подмножеств неизвестна, и определить значение средней стоимости алгоритма поиска невозможно. Поэтому значения средней стоимости заменяются их нижними границами Сн(S0) и Сн(S1) при контроле соответствующих параметров в подмножествах S0(zi) и S1(zi). Тогда нижняя граница средней стоимости всей программы поиска, которая начинается с контроля первого параметра, определяется как
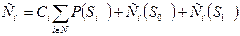 (47)
(47)
Вычислив нижние границы стоимостей Сн(S0) и Сн(S1) для всех возможных алгоритмов поиска, выбирают первым такой параметр, контроль которого дает минимальную среднюю стоимость нижней границы алгоритма поиска.
Затем для подмножеств S0(zi) и S1(zi) вычисляют нижние границы стоимостей для всех возможных пар контролируемых параметров между первым и оставшимися для каждого подмножества.
Пусть для подмножества S0(zi) контролируется параметр zк, а для подмножества S1(zi) – параметр zj. Тогда нижняя граница средней стоимости программы поиска, начинающейся с контроля i – параметра, будет:
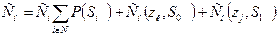 (48)
(48)
В общем виде записывается:
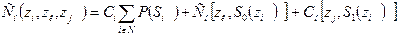 (49)
(49)
где 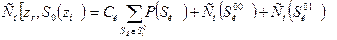 (50)
(50)
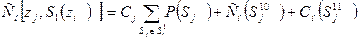 (51)
(51)
где 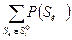 и
и 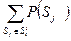 - суммы вероятностей в подмножествах
- суммы вероятностей в подмножествах 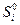 и
и 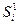 соответственно.
соответственно.
Значения 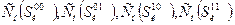 рассчитываются по формулам (46-48) для подмножеств
рассчитываются по формулам (46-48) для подмножеств 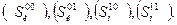
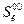 - подмножество состояний ОД, образующееся при отрицательном результате контроля параметров Zi
- подмножество состояний ОД, образующееся при отрицательном результате контроля параметров Zi и Zк;
и Zк;
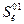 - подмножество состояний ОД, образующееся при отрицательном результате контроля параметра Zi
- подмножество состояний ОД, образующееся при отрицательном результате контроля параметра Zi и положительном результате контроля параметра Zк;
и положительном результате контроля параметра Zк;
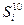 - подмножество состояний ОД, образующееся при положительном результате контроля параметра Zк и отрицательном результате контроля параметра Zi;
- подмножество состояний ОД, образующееся при положительном результате контроля параметра Zк и отрицательном результате контроля параметра Zi;
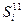 - подмножество состояний ОД, образующееся при положительном результате контроля параметром Zк и Zi;
- подмножество состояний ОД, образующееся при положительном результате контроля параметром Zк и Zi;
Вторым выбирается такой параметр, при контроле которого обеспечивается минимальная средняя стоимость нижней границы из всех возможностей алгоритмов поиска.
Аналогичным образом выбирают третий параметр и последующие параметры, пока получаемые пи контроле подмножества будут содержать более двух состояний ОД.
|
|
|



 Пример 3.7.4
Пример 3.7.4
 | |||||
| |||||
 |
Рис. 12 Функциональная модель ОД
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 599; Нарушение авторских прав?; Мы поможем в написании вашей работы!