
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод диагностики на основе ортогонального анализа отклика системы по базису гармонических функций
|
|
|
|
Известно, что динамические свойства любой радиотехнической системы можно описать её откликом h(t). Если отклик системы разложить в ряд Фурье и установить аналитическую связь между коэффициентами ряда Фурье для отклика и параметрами диагностируемой системы, то на этой основе можно проводить диагностирование. Отклик любой системы
 <
<  (59)
(59)
где М и С0 – постоянные положительные действительные числа:
h(t) = 0 при t < 0 и h(t)  0 при t > 0.
0 при t > 0.
Для отклика системы, удовлетворяющего условию (59) можно применить преобразование Лапласа:

(60)

где функция h(t) является оригиналом, а функция Н(р) является изображением функции по Лапласу.
Учитывая условие (59) в формулах (60) можно положить С = 0 и р = jω.
Тогда получим преобразование Фурье:
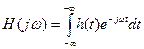
(61)

Разложение функции h(t) в ряде Фурье в комплексной форме имеет вид:
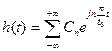 (62)
(62)
где t0 – для отклика h(t);
Сn – комплексные коэффициенты.

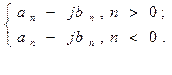 (63)
(63)
Из сравнения (60) и (63) получаем формулы для определения коэффициентов Фурье:
 , при
, при 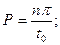 (64)
(64)
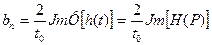 , при
, при  (65)
(65)
Используя преобразование Лапласа, можно получить изображение выходного сигнала и передаточной функции.
S2 (P) = S1 (P)*K(p) (66)
Зная параметры элементов системы, можно вычислить её передаточную функцию К(р). Если параметры входного сигнала S1(P) будут неизменными, то любые отклонения параметров системы за допустимые пределы будут отражаться в спектре выходного сигнала.
Связь между параметрами системы и коэффициентами ряда Фурье разложения передаточной функции можно продемонстрировать на примере.
Пример 3.9.5 Передаточная функция видеосигнала.
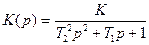 (67)
(67)
где {х} = К, Т1, Т2 – диагностируемые параметры (вторичные).
Решение. Определить вещественную и мнимую часть передаточной функции:
 ;
;
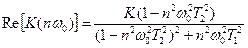 ;
;
 ;
;
ω = n*ω0, где n – номер гармоники;
ω0 – частота основной гармоники.
Для определения текущих значений диагностируемых параметров, составим систему уравнений, используя действительную часть передаточной функции:
 ;
;
(68)
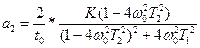 .
.
Используя мнимую часть передаточной функции, получим другую систему уравнений:
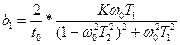 ;
;
(69)
 .
.
В дальнейшем для упрощения вычислений используем относительные коэффициенты разложения:
В1 = b1/ a 1; B2 = b2/ a 2; …; Bn = bn/ a 2. (70)
Используя текущие значения в относительных коэффициентов, составим систему уравнений:
 (71)
(71)
Систему уравнений приведем к виду:
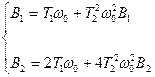 (72)
(72)
Решая систему уравнений (71) и (72) относительно Т1 и Т2, получим выражения для параметров диагностируемой системы:
 (73)
(73)
Для определения коэффициента усиления К видеоусилителя воспользуемся уравнением:
 . (74)
. (74)
Отсюда:
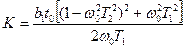 . (75)
. (75)
Полученные значения параметров сравниваются с их номинальными значениями. Параметр, вышедший из допуска, и определяет место неисправности.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 357; Нарушение авторских прав?; Мы поможем в написании вашей работы!