Лабораторная работа №3

Численное интегрирование

3.1 Постановка задачи численного интегрирования.

Основные понятия

Пусть вычисляется интеграл 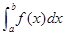, причем функция 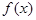такова, что неопределенный интеграл от неё или не вычисляется в элементарных функциях или функция 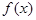задана в виде таблицы. Вместо слов, численное вычисление определённых интегралов, часто используют термин вычисление квадратур, дабы избежать путаницы с численным интегрированием обыкновенных дифференциальных уравнений и по этой причине формулы приближенного вычисления интегралов называют квадратурными формулами.

Пусть [ a, b ] конечный интервал оси х разбит на n интервалов, которые называются элементарными отрезками или подинтервалами [. Положим 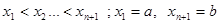, а через обозначим длину i -го элементарного отрезка, тогда

, (1)

который можно представить в виде 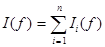, разбивая промежуток интегрирования, где интеграл по подинтервалу.

Аналитическую формулу, дающую приближённое значение называют простой (элементарной) квадратурной формулой, а формулу, дающую значение , называют составной квадратурной формулой.

Итак, задача численного интегрирования состоит в вычислении приближённого значения интеграла (1),т.е. в построении составной квадратурной формулы, проведении численного расчета и оценке погрешности вычислений.

3.2 Основные методы построения квадратурных формул.

Наиболее распространённые методы построения квадратурных формул основаны на использовании аппарата интерполирования, либо получаются, на основе интерполяционных формул, методом неопределённых коэффициентов.

Рассмотрим простейший пример построения элементарных квадратур методом неопределённых коэффициентов. Без ограничения общности можем рассматривать элементарный отрезок [- h, h ] и количество узлов в нём выбирать, исходя из точности квадратуры.

Приведём рассмотрение случаев одного, двух и трёх узлов на отрезке [- h, h ] при построении квадратурных формул, которые будут точны, соответственно, на полиномах нулевой, первой и второй степеней[1].

а) Квадратурная формула, точная для многочленов нулевой степени (формула прямоугольников).

Эта квадратура может быть получена из интерполяционного полинома построенного по одному узлу. Т.е. элементарная квадратура имеет вид следующего равенства:

,

с неопределенным коэффициентом 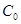.Погрешность этой квадратуры равная

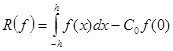, (2)

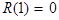должна обращаться в нуль на многочленах нулевой степени, т.е. при мы должны иметь , т.к. 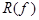является линейным функционалом. Для получаем уравнение из равенства (2)

,

т.е. имеем простую квадратуру

,

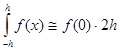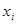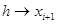которую легко обобщить для i -го элементарного интервала, по следующей схеме: соответствует нижнему пределу интегрирования i -го элементарного интервала , , соответствует средина промежутка интегрирования

. (2а)

Легко установить геометрический смысл этой квадратуры, (из которого становится очевидным название квадратуры- как формулы прямоугольников). Из приведенного ниже рисунка, где наклонными линиями заштрихована фигура, площадь которой равна а вертикальными линиями заштрихован прямоугольник с площадью даваемой квадратурной формулой (2а)

Рис.1

б) Квадратурная формула, точная для многочленов первой степени (формула трапеций).

В этом случае мы должны строить квадратуру по двум узлам - h, h.

.

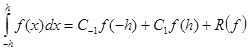Неопределённые коэффициенты 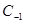и 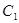мы определим из условия обращения в нуль и

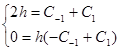
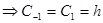
Таким образом, имеем простую квадратуру

,

которая легко обобщается для любого i -го элементарного подинтервала

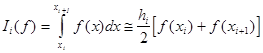. (2б)

Геометрический смысл этой формулы (дающей ей название формулы трапеций) легко установить из приведённого ниже рисунка, где наклонными линиями заштрихована фигура, площадь которой равна , а вертикальными линиями заштрихована трапеция с площадью даваемой квадратурной формулой (2б)

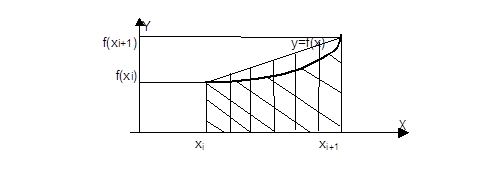
Рис.2

в) Квадратурная формула, точная для многочленов второй степени (формула Симпсона или формула парабол).

В этом случае мы должны строить квадратуру уже по трем узлам - h, 0, h

.

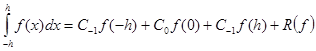Из условия обращения в ноль получаем систему трёх уравнений на коэффициенты

Решая эту систему, получаем

.

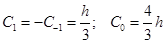Таким образом, элементарная квадратура имеет вид

,

ее обобщение для i -го элементарного подинтервала имеет вид

.

Аналогично предыдущему можно провести геометрическую интерпретацию формулы Симпсона (2в). Предлагается выполнить это задание самостоятельно. Окончательно выпишем элементарные квадратуры для всех рассмотренных случаев:

а) формула прямоугольников ;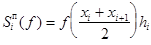

б) формула трапеций ;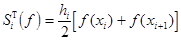

в) формула Симпсона .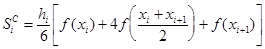

Мы установили, что эти квадратурные формулы являются точными соответственно для полиномов 0-й, 1-й и 2-й степеней, но нет никаких ограничений, которые бы запрещали этим формулам быть точными для полиномов более высоких степеней, что мы и увидим позже, когда займёмся оценкой погрешностей квадратурных формул.

Задачи для самостоятельного решения.

1. Построить квадратурные формулы исходя из аппарата интерполирования.

2. Построить квадратуры прямоугольников и трапеций, непосредственно вычисляя площади фигур, получаемых в результате разбиения.

3. Типичной задачей прикладной математики является отыскание решения интегрального уравнения

,

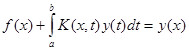где и заданы, а задача состоит в вычислении .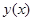

Если мы приблизим интеграл посредством квадратурной формулы

,

то интегральное уравнение превратится в систему линейных алгебраических уравнений. Ее решение 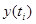, , есть искомое дискретное приближение к функции .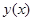

Используя формулу Симпсона, постройте приближенную систему для интегрального уравнения

.

Сравните полученное решение с точным в различных точках интервала .

4. Найдите веса формулы Ньютона-Котеса 8-го порядка, потребовав, чтобы приближенное равенство

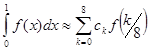
было точным для , .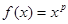

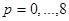3.3 Оценка погрешности квадратурных формул

В этом параграфе найдём оценки точности полученных элементарных квадратурных формул сначала на интервале [ -h, h ], а затем проведём обобщение на произвольный элементарный интервал.

Введём в рассмотрение остаточный член квадратурной формулы, называемый также ее невязкой , дающий точность квадратурных формул.

1. Формула прямоугольников.

, ,

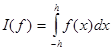. (3.1)

Разложим функцию f(x) в точке x =0 в ряд Тейлора по x с точностью до членов второго порядка:

, где .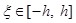

Подставляя это выражение в (3.1), получим

.

Предельная абсолютная погрешность квадратуры прямоугольников может быть выписана в виде

или .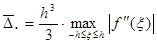

Производя естественное обобщение на случай произвольного элементарного интервала, получим, с учётом , оценку предельной погрешности вычисления интеграла для i -го подинтервала

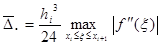. (3.2)

Из полученной формулы видим, что она является точной и для многочленов первой степени.

2. Формула трапеций.

Аналогично проведём оценку погрешности формулы трапеций.

Разложим функции f (x), f (-h) и f (h) в ряд Тейлора в точке x=h=0:

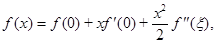
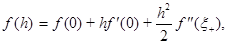
где , , .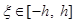

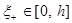С учётом полученных разложений имеем

Член с производными можно упростить, предполагая непрерывной. По свойству среднего арифметического

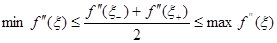
оно является промежуточным значением производной в некоторой точке 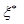интервала, т.е.

,

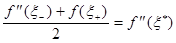на основании теоремы о промежуточных значениях непрерывной функции. Точное значение интеграла от функции f (x) на отрезке [- h, h ] будет равно

.

Поэтому величина R (f) получится равной

Следовательно, предельная абсолютная погрешность формулы трапеций может быть оценена следующим образом

,

.

Для произвольного элементарного подинтервала имеем

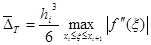
Полученная формула также подтверждает, что квадратура трапеций является точной для многочленов первой степени.

3. Формула Симпсона.

Оценку точности квадратурной формулы проведём аналогично тому, как это делалось для формулы трапеций.

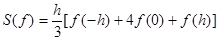
Функции f (x), f (-h) и f (h) разложим в ряд Тейлора в точке x =0, сохраняя в их разложении, только пять первых членов:

;

;

.

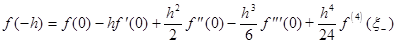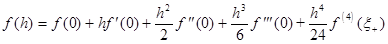В этом случае будем иметь:

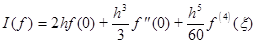
и

.

Оценку точности, как обычно, определим по формуле

,

откуда получаем искомую предельную абсолютную погрешность квадратуры Симпсона для интервала [ -h, h ]

.

Для обобщения полученной оценки погрешности на случай произвольного подинтервала следует интервал [ a, b ] разделить на чётное число подинтервалов n = 2m, и тогда оценку погрешности можно записать в виде

.

Из приведённой формулы видно, что квадратура парабол будет точной и для многочленов третьей степени.

3.4 Составные квадратурные формулы

Получим составные квадратурные формулы прямоугольников, трапеций и Симпсона для интервала [ a, b ], приведём оценку их погрешностей и укажем способ Ричардсона приближённой оценки погрешностей названных квадратурных формул.

Как обычно, рассмотрение проведём для каждого случая отдельно.

1. Формула прямоугольников

Погрешность вычислений по этой формуле не будет превышать величины

,

где

Для равноотстоящих узлов формула прямоугольников и соответствующая ей погрешность будут иметь вид:

,

где .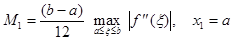

Приведённая формула и оценка погрешности удобны для численных расчётов на ЭВМ.

2. Формула трапеций

Составная квадратурная формула прямоугольников имеет вид:

.

Поскольку при суммировании по интервалам все внутренние точки встречаются дважды, приведём формулу для случая равноотстоящих узлов в двух видах:

,

.

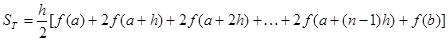Погрешность расчёта по этим формулам будет равна ,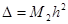

где .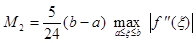

3. Формула Симпсона

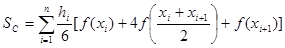
Поскольку при суммировании все внутренние узлы интервала [ a, b ] встречаются дважды, составная квадратурная формула для равноотстоящих узлов будет иметь вид:

,

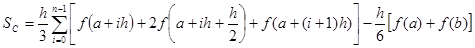где , , .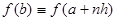

3.5 Метод Ричардсона практической оценки точности квадратурных формул

Рассмотрим приближённый метод оценки точности квадратурных формул. Приближённость метода состоит в том, что он корректен только для некоторого класса функций и полученные формулы для погрешности работают с точностью, до главных членов[2]. Мы же будем применять его для любых функций.

Пусть 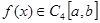, при этом предположении мы получим уточнение формулы прямоугольников. Производя разложение в ряд Тейлора с точностью до членов четвертого порядка по 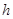получим

,

где постоянная величина независящая от 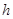, а элементарная квадратура прямоугольников. Величина 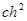называется главной частью погрешности формулы прямоугольников. При этих же предположениях, для формулы трапеций справедливо соотношение , где элементарная квадратура трапеций. Для формулы Симпсона, при условии имеет место равенство .Т.е. для любой квадратурной формулы можно выписать соотношение

. (1)

Тогда, выписывая это соотношение на шаге 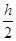, имеем

. (2)

Вычитая из (1) равенство (2), получим

.

Отсюда

и, следовательно, согласно (2) имеем с точностью до

, (3)

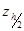и 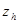известные величины*, причем величина погрешности· равна ¨.

Замечание На практике подтверждением условия является выполнение неравенства

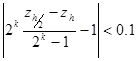. (4)

Неравенство (4) может нарушаться последующим причинам: а) 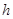велико, при этом влияет отброшенный член ; б) 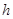слишком мало, тогда могут сказаться погрешности арифметики реальной ЭВМ; в) или близко к нулю.

Задачи для самостоятельного решения.

1. Используя равенство

найти с помощью численного интегрирования приближения к числу 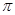. Использовать формулу прямоугольников и формулу трапеций с элементарными отрезками одинаковой длины , взяв 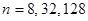. Для данных 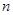результат записать со всеми верными цифрами.

2. Для интеграла 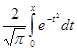построить таблицу значений, с точностью , допускающую линейную интерполяцию.

3. Используя определение интеграла Римана и теорему о среднем значении интеграла, доказать, что приближения, получаемые из квадратур прямоугольников и трапеций, сходятся при к интегралу. Выделите отчетливо те предположения, которые делаются относительно подынтегральной функции.

4. Какой результат будет получен квадратурой Симпсона, с точностью 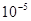, для интеграла ? Каков точный результат?

5. Опишите эффективный и “точный” метод вычисления интеграла , где

.

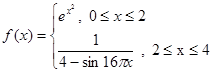Задания к лабораторной работе.

№	f(x)	a	b
		1.7	3.3	10^-8
		40.0	43.6	10^-8
		2.6	5.0	10^-8
		2.6	16.8	10^-8
		1.5	3.1	10^-8
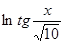
		1.8	3.4	10^-8
		0.7	1.5	10^-8
		7	15	10^-8
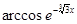
		0.20	0.56	10^-8
		2.2	7.0	10^-8
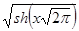
		1.50	2.22	10^-8
		0.5	1.7	10^-8
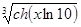
		1.5	3.1	10^-8
		2	6	10^-8
		2.0	5.2	10^-8
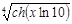
		1.5	3.1	10^-8
		1.5	3.1	10^-8
		2.0	6.0	10^-8
№	f(x)	a	b
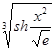
		2	6	10^-8
		2.2	7.0	10^-8
		2.21	7.01	10^-8

1. Квадратурами прямоугольников, трапеций и Симпсона вычислить интегралы с заданной точностью. Пояснить, почему получается такое число подинтервалов?

2. Построить таблицу значений интеграла , где принимает десять значений из промежутка , допускающую линейную интерполяцию. Результат должен быть представлен со всеми верными цифрами.

Контрольные вопросы к лабораторной работе.

Литература

1. Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. Численные методы. М:, Наука, 1987.

2. Дж. Форсайт, М. Малькольм, К. Моулер Машинные методы математических вычислений. М., “Мир” 1980.

3. В.В. Воеводин Вычислительные основы линейной алгебры. М., “Наука”, 1977.

4. Е.А. Волков Численные методы. М., “Наука”, 1987.

5. Л.З. Румшиский Вычислительный лабораторный практикум. М., ГИФМЛ 1961.

[1] Применимость этого метода основана на факте, что интерполяционный полином построенный по узлам, приближает с нулевой погрешностью все полиномы степени не выше

[2] Это требование не является обременительным т,к, в погрешности мы не оставляем более двух значащих цифр.

* При условии.

· С такой же точностью.

¨ Эта оценка и называется правилом Рунге.

Дата добавления: 2014-01-05