Натуральная величина отрезка прямой общего положения. Метод прямоугольного треугольника

Деление отрезка в заданном отношении

Теорема Фалеса:

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Используя эту теорему можно легко разделить любой отрезок в заданном отношении.

Рис. 2.13

В отличие от отрезков прямых частного положения, проецирующихся хотя бы на одну из плоскостей проекций в натуральную величину, отрезок прямой общего положения на плоскости проекций проецируется с искажением. Для того, чтобы найти его натуральную величину необходимо провести ряд преобразований. Существует несколько методов нахождения натуральной величины отрезка прямой общего положения и углов наклона его к плоскостям проекций. Одним из этих методов является метод прямоугольного треугольника, в котором находится зависимость длины проекции отрезка от его истинной величины.

Возьмем прямую общего положения АВ и спроецируем ее на горизонтальную плоскость проекций P₁. Через точку А проведем линию, параллельную плоскости P₁. Таким образом в пространстве получим прямоугольный треугольник АВВ’, один из катетов которого (АВ’) равен длине проекции отрезка, а угол, между отрезком и этим катетом является углом наклона заданного отрезка к плоскости проекций (рис. 2.14).

Рис. 2.14

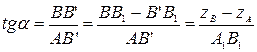
Для определения натуральной величины отрезка прямой общего положения и углов наклона ее к плоскости проекций на КЧ необходимо построить прямоугольный треугольник:

1. Первый катет этого треугольника равен проекции отрезка на плоскости проекций (обычно прямоугольный треугольник пристраивают к проекции отрезка, однако в некоторых задачах целесообразно прямоугольный треугольник строить в стороне от проекций геометрических объектов).

2. Из проекции любого конца отрезка (А₁ или В₁) под прямым углом к проекции отрезка проводится луч, на котором откладывается длина второго катета, равная разности расстояний от концов отрезка до данной плоскости проекций.

3. Гипотенуза полученного таким образом прямоугольного треугольника равна длине заданного отрезка.

4. Угол наклона отрезка к той или иной плоскости проекций равен углу между гипотенузой - натуральной величиной и катетом – проекцией на эту плоскость проекций.

Следовательно, для определения угла наклона отрезка к горизонтальной плоскости проекций, прямоугольный треугольник строится на базе горизонтальной проекции отрезка, к фронтальной плоскости проекций – на базе фронтальной плоскости, к профильной плоскости проекций – на базе профильной проекции.

Рис. 2.15

Дата добавления: 2014-01-05