Спосіб заміни площин проекцій

Нехай ми маємо якийсь об’єкт, наприклад, точку А, яка спроекційована на дві площини проекцій П₁ та П₂ (рис. 6.4). З якоїсь причини нас не влаштовують проекції А₁ і А₂. Необхідно перетворити креслення, замінивши одну з площин проекцій, наприклад, П₂. Введемо нову площину П₄, перпендикулярну до площини П₁. При цьому утворилась нова система

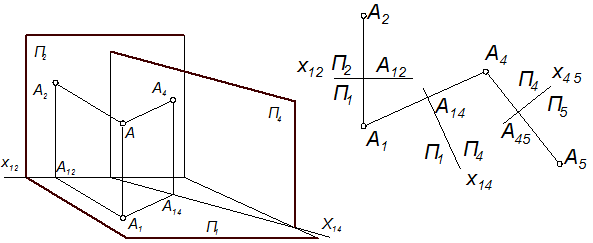площин проекцій П₁/П₄ з новою віссю проекцій x₁₄. Спроекціюємо ортогонально точку А на нову площину проекцій, маємо проекцію А₄. Звернімо увагу на те, що висота Z_A точки А однаково без спотворення проек

Рис. 6.4 Рис. 6.5

ціюється і на площину П₂ («стару») і на площину П₄ («нову»). Ця обставина і використовується для побудови нової проекції А₄.

Суть способу заміни площин проекцій полягає у заміні однієї площини проекцій іншою, перпендикулярною до тієї, що залишається. У такому разі від старої системи площин проекцій П₁/П₂ залишається одна площина проекцій і все, що з нею пов’язане, а саме проекція предмета на цю площину і відстані від точок предмета до цієї площини.

Покажемо суть способу на прикладі конкретної точки А (рис. 6.5). Введемо нову площину проекцій П₄, провівши якимось чином нову вісь проекцій x₁₄. Через проекцію А₁ точки А проведемо нову лінію зв’язку перпендикулярно до осі x₁₄ і на ній відкладемо відрізок А₁₄А₄, який становить висоту точки А і дорівнює відрізкові А₂А₁₂. Може виникнути потреба у подальшому перетворенні креслення заміною і площини П₁ новою площиною - П₅, перпендикулярною до площини П₄. У такому разі проводимо нову вісь проекцій x₄₅ і через проекцію А₄ проводимо нову лінію зв’язку перпендикулярно до неї. На цій лінії відкладаємо відрізок А₄₅А₅, який дорівнює відрізкові А₁А₁₄, тобто відстані від точки А до площини П₄. Маємо “нову” проекцію А₅ точки А.

Далі покажемо застосування способу заміни площин проекцій для розв’язування чотирьох основних задач.

Задача 1. Перетворити креслення так, щоб пряма АВ(А₁В₁, А₂В₂) загального положення стала лінією рівня (рис. 6.6).

Для цього необхідно одну з площин проекцій, наприклад, П₂, замінити новою площиною П₄, паралельною прямій АВ. Проводимо нову вісь проекцій x₁₄ паралельно проекції А₁В₁ прямої АВ на довільній від неї відстані і за лініями зв’язку, перпендикулярними до осі x₁₄, знаходимо нові проекції А₄ і В₄ точок А і В: А₁₄А₄ = А₂А₁₂, В₁₄В₄ = В₂В₁₂. Сполучаємо точки А₄ і В₄, маємо проекцію А₄В₄ відрізка АВ. Довжина проекції А₄В₄ дорівнює довжині самого відрізка АВ, тобто відрізок АВ спроекціювався на площину проекцій П₄ без спотворення. Крім того, кут нахилу проекції А₄В₄ до осі x₁₄ становить кут нахилу прямої АВ до площини проекцій П₁. Щоб визначити кут нахилу прямої Рис. 6.6

АВ до площини проекцій П₂,

необхідно замінити площину П₁ новою площиною проекцій, перпендикулярною до площини П₂ і паралельною прямій АВ.

Задача 2. Перетворити креслення прямої загального положення так, щоб вона стала проекціювальною прямою.

Нову площину проекцій не можна поставити зразу перпендикулярно до прямої АВ, бо за умовою способу заміни ця площина має бути перпендикулярною до тієї площини проекцій, що залишається. Тому, щоб пряму загального положення перетворити на проекціювальну, необхідно послідовно замінити обидві площини проекцій П₁ і П₂, перетворивши спочатку пряму у лінію рівня, а потім – у проекціювальну пряму. Таким чином, задача 1 входить до складу задачі 2 як її перша складова частина. На рис. 6.6 після заміни площини П₂ замінено площину П₁ на нову площину проекцій П₅, перпендикулярну до площини П₄ і прямої АВ. Нова вісь проекцій x₄₅ проведена перпендикулярно до проекції А₄В₄ прямої АВ і за лінією зв’язку, перпендикулярною до осі x₄₅ знайдена нова проекція А₅=В₅ прямої АВ: А₅А₄₅ = А₁А₁₄ = В₅В₄₅ = В₁В₁₄.

На основі другої задачі можна визначити відстань від точки до прямої, між двома прямими (паралельними чи мимобіжними), двогранний кут між площинами, якщо відома лінія їхнього перетину і т. ін.

Для прикладу на рис. 6.6 визначена відстань від точки М(М₁, М₂) до прямої АВ. Після послідовної заміни площин проекцій П₂ і П₁ на нові площини П₄ і П₅ та побудови проекції А₅=В₅ прямої АВ аналогічно знаходимо нові проекції М₄ та М₅ точки М. Відрізок М₅А₅ становить відстань від точки М до прямої АВ.

Задача 3. Перетворити креслення площини загального положення так, щоб вона стала проекціювальною площиною.

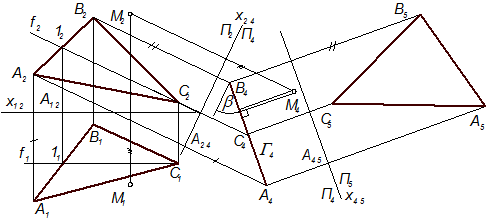Для цього необхідно нову площину проекцій поставити перпендикулярно до лінії рівня заданої площини. На рис. 6.7 показано перетворення

креслення площини Г(DАВС), де замінена площина П₁ на нову площину П₄ ^ П₂. Площина П₄ ^ f Ì Г: x₂₄ ^ f₂. На лініях зв’язку, Рис. 6.7

перпендикулярних до осі x₂₄, від останньої відкладені координати y_A, y_B та y_C. Так, на лінії зв’язку А₂А₄ ^ x₂₄ від точки А₂₄ відкладений відрізок А₁А₁₂, маємо точку А₄. Точки В₄ і С₄ побудовані аналогічно. Оскільки площина П₄ перпендикулярна до площини Г, то остання зобразилась у пряму лінію. На основі третьої задачі можна визначити відстань від точки чи прямої до площини і між двома паралельними площинами, а також кути нахилу площини до площин проекцій. На рис. 6.7 показано визначений кут b між площиною Г(DАВС) і площиною П₂. Крім того, визначена дійсна величина відстані від точки М до площини Г. Слідом за побудовою проекції Г₄ площини Г побудована і проекція М₄ так, як це зроблено для проекції А₄ точки А. Перпендикуляр, проведений від точки М₄ до проекції Г₄ площини Г, визначає дійсну величину відстані від точки М до площини Г.

Задача 4. Перетворити креслення площини загального положення так, щоб вона стала площиною рівня.

Для цього необхідно спочатку перетворити задану площину на проекціювальну (задача 3), а потім заміною другої площини проекцій можна привести задану площину у положення площини рівня.

На рис. 6.7 після того, як розв’язана задача 3 (площина Г(DАВС) приведена у положення проекціювальної), замінено площину П₂ на П₅, перпендикулярну до площини П₄. Площина П₅ поставлена паралельно площині Г, тому вісь x₄₅ êêГ₄(А₄В₄С₄).

На лінії зв’язку А₄А₅ відкладений відрізок А₄₅А₅ = А₂А₂₄. Аналогічно побудовані проекції В₅ і С₅ точок В і С. Трикутник А₅В₅С₅ конгруентний заданому трикутнику АВС. Тому на основі четвертої основної задачі можна визначити неспотворену проекцію плоскої фігури, а також дійсну величину кута між двома прямими загального положення (мимобіжними чи такими, що перетинаються).

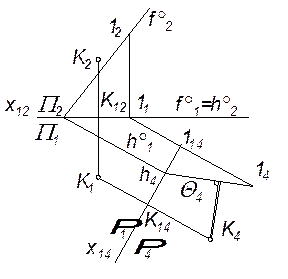Розв’язування задачі 3 значно спрощується, якщо площина задана своїми слідами. На рис. 6.8 показано визначення відстані від точки К(К₁, К₂) до площини Q(h°, f°). Для цього площина проекцій П₂ замінена на площину П₄, яка перпендикулярна до горизонтального сліду h° площини Q: x₁₄ ^ h°₁.

На фронтальному сліді f° взята довільна точка 1(1₁, 1₂) і побудована її проекція 1₄ на площині П₄: 1₁1₄ ^ x₁₄, 1₁₄1₄ = 1₂1₁₂. Площина Q спроекціювалась у пряму Q₄, яка проходить через точки h₄ і 1₄. Рис. 6.8

Проекція К₄ точки К побудована аналогічно точці 1₄: К₁К₄ ^ x₁₄, К₁₄К₄ = К₂К₁₂. Перпендикуляр, проведений від точки К₄ до проекції Q₄ площини Q, визначає дійсну величину відстані від точки К до площини Q.

Дата добавления: 2014-01-05