
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Деформативность бетона
|
|
|
|
Деформации могут быть силовые, развивающиеся под действием внешних сил, и температурно-влажностные, развивающиеся, в результате взаимодействия бетона с внешней средой.
Деформации бетона под нагрузкой. Различают силовые деформации при однократном кратковременном, длительном, а также многократно-повторном нагружениях.
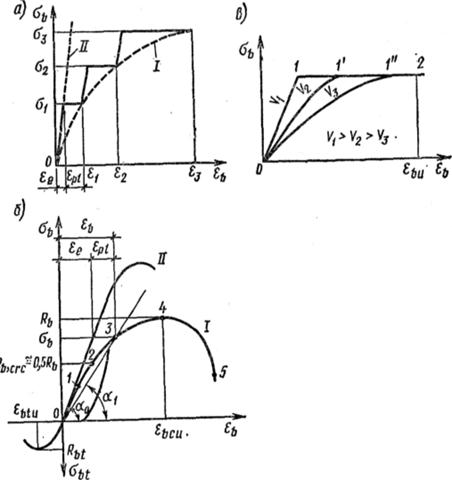
Рисунок 1.3 – Диаграммы деформирования бетона: а) – при ступенчатом нагружении; б) – кривая полных деформаций; в) – при длительном нагружении; I – полные деформации; II – при мгновенном нагружении
1. Деформации при однократном кратковременном нагружении. Наибольшее практическое значение имеют деформации при осевом сжатии. Если бетонную призму нагружать по этапам, замеряя деформации дважды: сразу после приложения нагрузки и через некоторое время после выдержки под нагрузкой, то на диаграмме « » получают ступенчатую линию (рис. 1.3,а). Полные деформации будут складываться из упругих
» получают ступенчатую линию (рис. 1.3,а). Полные деформации будут складываться из упругих 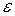 е, возникающих непосредственно после приложения нагрузки, и пластических
е, возникающих непосредственно после приложения нагрузки, и пластических 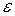 Р1, развивающихся во времени. Кривая полных деформации показана на рис. 1.3,б. Из диаграммы видно, что при небольших напряжениях (
Р1, развивающихся во времени. Кривая полных деформации показана на рис. 1.3,б. Из диаграммы видно, что при небольших напряжениях (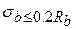 ) бетон можно рассматривать как упругий материал (участок 0 —/). При
) бетон можно рассматривать как упругий материал (участок 0 —/). При 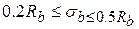 возникают неупругие деформации, вызванные уплотнением геля (участок /— 2). После образования микротрещин Rb,crc рост пластических деформаций становится более интенсивным (участок 2 — 3). При дальнейшем увеличении нагрузки микротрещины объединяются и образец разрушается — точка 4 соответствует предельному сопротивлению образца Rb и деформациям
возникают неупругие деформации, вызванные уплотнением геля (участок /— 2). После образования микротрещин Rb,crc рост пластических деформаций становится более интенсивным (участок 2 — 3). При дальнейшем увеличении нагрузки микротрещины объединяются и образец разрушается — точка 4 соответствует предельному сопротивлению образца Rb и деформациям 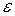 ь,си. Если по мере падения сопротивления бетона удается в той же мере снижать нагрузку, то может быть получен нисходящий участок диаграммы (4 —5). Знать, как работает бетон на этом участке, важно для ряда конструкций и видов нагружения.
ь,си. Если по мере падения сопротивления бетона удается в той же мере снижать нагрузку, то может быть получен нисходящий участок диаграммы (4 —5). Знать, как работает бетон на этом участке, важно для ряда конструкций и видов нагружения.
При разгрузке с некоторого уровня напряжений, соответствующего восходящей ветви, до нуля в образце будут иметь место остаточные деформации, которые со временем несколько уменьшаются (примерно на 10%). Это явление называется упругим последействием 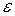 ер. Характер диаграммы «
ер. Характер диаграммы « » бетона при растяжении аналогичен рассмотренному (рис. 1.3,б).
» бетона при растяжении аналогичен рассмотренному (рис. 1.3,б).
Связь между напряжениями и деформациями при небольших напряжениях (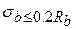 ) устанавливается законом Гуна
) устанавливается законом Гуна 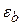 =
=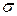 ь/Еb, где Еb — начальный модуль упругости, Еb = tg
ь/Еb, где Еb — начальный модуль упругости, Еb = tg =
=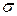 b/
b/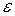 ь (см. рис. 1.3,б). Модуль упругости зависит от марки бетона (см. табл. 2.1). При
ь (см. рис. 1.3,б). Модуль упругости зависит от марки бетона (см. табл. 2.1). При 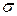 b >0,2 Rb (зависимость «
b >0,2 Rb (зависимость « » нелинейная, модуль в каждой точке диаграммы — переменный, Еb =d
» нелинейная, модуль в каждой точке диаграммы — переменный, Еb =d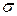 /d
/d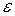 = tg
= tg и определение полных деформаций является затруднительным.
и определение полных деформаций является затруднительным.
Для практических расчетов было предложено выражать напряжения через полные деформации бетона с помощью упругопластического модуля деформаций Еb,pl = tg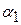 (см. рис. 1.3,б).
(см. рис. 1.3,б).
Выразив одно и то же напряжение в бетоне через упругие и полные деформации, получают
откуда (1.5)
где  — коэффициент, характеризующий упруго-пластическое состояние сжатого бетона; он изменяется от 1 (при упругой работе) до 0,45 при кратковременном нагружении; при длительном действии нагрузки
— коэффициент, характеризующий упруго-пластическое состояние сжатого бетона; он изменяется от 1 (при упругой работе) до 0,45 при кратковременном нагружении; при длительном действии нагрузки 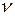 = 0,1...0,15.
= 0,1...0,15.
При растяжении (1.6)
где 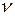 t — коэффициент, характеризующий упругопластическое состояние бетона при растяжении,
t — коэффициент, характеризующий упругопластическое состояние бетона при растяжении, 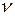 t = 0,5. Модуль сдвига бетона:
t = 0,5. Модуль сдвига бетона:
(1.7)
где 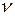 — коэффициент поперечных деформаций, для всех видов бетонов
— коэффициент поперечных деформаций, для всех видов бетонов 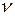 = 0,2, при этом Gb =0,4 Еb.
= 0,2, при этом Gb =0,4 Еb.
2. Деформации при длительном действии нагрузки. При длительном действии нагрузки неупругие деформации бетона с течением времени увеличиваются. Наибольшая интенсивность нарастания неупругих деформаций наблюдается в первые 3...4 мес.
Ползучестью называют свойство бетона увеличивать неупругие деформации при длительном действии постоянной нагрузки. Различают ползучесть линейную и нелинейную. Линейная ползучесть имеет место при 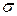 b < 0,5 Rb и обусловлена главным образом уплотнением геля. При этом происходит перераспределение под нагрузкой напряжений с гелевой структуры на цементный камень и заполнители. Увеличение деформаций ползучести примерно пропорционально увеличению напряжений. При
b < 0,5 Rb и обусловлена главным образом уплотнением геля. При этом происходит перераспределение под нагрузкой напряжений с гелевой структуры на цементный камень и заполнители. Увеличение деформаций ползучести примерно пропорционально увеличению напряжений. При 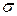 b > 0,5 Rb в бетоне возникают микротрещины, линейная зависимость
b > 0,5 Rb в бетоне возникают микротрещины, линейная зависимость 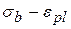 нарушается, наступает нелинейная ползучесть,
нарушается, наступает нелинейная ползучесть,
Ползучесть бетона затухает во времени, так как вследствие перераспределения усилий напряжения в геле снижаются, а упругость кристаллического сростка возрастает.
Опыты показывают, что независимо от того, с какой скоростью v достигнуто напряжение 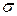 b, конечные деформации ползучести, соответствующие этому напряжению, будут одинаковыми (рис. 1.3,в).
b, конечные деформации ползучести, соответствующие этому напряжению, будут одинаковыми (рис. 1.3,в).
Деформации ползучести увеличиваются с уменьшением влажности среды, увеличением В/Ц и количества цемента. Бетон, нагруженный в более раннем возрасте, обладает большей ползучестью. С повышением прочности бетона и прочности заполнителя ползучесть уменьшается. У малых образцов при прочих равных условиях ползучесть проявляется сильнее, чем у больших.
Для аналитического описания явления ползучести предложены различные теории. Однако полученные на их основе математические зависимости сложны для использования в практических расчетах и в большинстве своем справедливы лишь для определенных условий. Поэтому на практике применяют упрощенные, линейные зависимости, связывающие напряжения в бетоне с деформацией ползучести. Правомерность такого подхода подтверждается и тем обстоятельством, что при эксплуатационных нагрузках в большинстве конструкций напряжения в сжатом бетоне 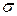 b < 0,5 Rb, т.е. имеет место линейная ползучесть.
b < 0,5 Rb, т.е. имеет место линейная ползучесть.
Для количественного определения деформаций ползучести при сжатии обычно вводят понятия меры и характеристики ползучести.
Мера ползучести Сt представляет собой относительную деформацию ползучести в момент времени t, соответствующую приращению напряжения 0,1 МПа. При напряжениях в бетоне 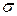 b
b
(1.8)
• Характеристика ползучести  равна отношению деформаций ползучести в момент времени t к мгновенной деформации
равна отношению деформаций ползучести в момент времени t к мгновенной деформации
(1.9)-
Предельные значения Сt и  будут при t=
будут при t= •(Сt =
•(Сt = =С;
=С; 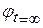 =
= ). Между мерой и характеристикой ползучести существует связь
). Между мерой и характеристикой ползучести существует связь
откуда. Значения  для обычных тяжелых бетонов изменяются в пределах 1...4.
для обычных тяжелых бетонов изменяются в пределах 1...4.
Предельные деформации бетона, т.е. деформации перед разрушением, зависят от многих причин и изменяются в значительных пределах. Для расчетов принимают: при осевом кратковременном сжатии  = 2·10-3, длительном
= 2·10-3, длительном  = 2,5·10-3, при изгибе и внецентренном сжатии
= 2,5·10-3, при изгибе и внецентренном сжатии  = 3,5·10-3, при центральном растяжении
= 3,5·10-3, при центральном растяжении  =1,5·10-4.
=1,5·10-4.
Деформации при многократно-повторных нагружениях. Многократно-повторные нагружения и разгрузки бетонных образцов приводят к накапливанию неупругих деформаций. После достаточно большого количества циклов пластические деформации достигают предельного значения и бетон начинает работать упруго. Такой характер работы имеет место, когда напряжения в бетоне не превышают предела выносливости. При больших многократных напряжениях неупругие деформации возрастают, вызывая разрушение образца.
Температурно-влажностные деформации бетона:
1. Деформации бетона от действия температуры. Твердение бетона сопровождается выделением теплоты, и при последующем неравномерном остывании появляются значительные температурные деформации. Температурные деформации возникают также в конструкциях, подверженных атмосферным воздействиям или изменениям технологических температур. Особое значение имеют температурные воздействия на бетон массивных конструкций (например, гидротехнических) и статически неопределимых систем большой протяженности, вызывая дополнительные усилия в элементах (см. рис. 11.4). Определение температурных деформаций бетона производят по формулам сопротивления материалов, принимая средний коэффициент линейной температурной деформации при —50°С< t <+50°С равным 1·10-5 град-1.
2. Влажностные деформации бетона. Бетон, твердея в различных средах, изменяет свой объем.
Свойство бетона уменьшаться в объеме при твердении в сухой среде называют усадкой, при твердении во влажной среде бетон увеличивается в объеме — происходит набухание. Различают усадку обратимую — связанную с испарением свободной воды в цементном камне и обусловленную капиллярными явлениями (натяжением менисков в порах бетона), и необратимую, происходящую в результате потери химически связанной влаги на гидратацию цемента и, как следствие, уменьшения объема геля.
Усадка зависит от возраста бетона: наиболее интенсивно она протекает в первые дни, затем постепенно затухает. Усадка тем больше, чем больше содержание в бетоне цемента, воды и чем ниже влажность окружающей среды. При твердении в воде увеличивается количество свободной воды в цементном камне, что вызывает явление, обратное усадке, — набухание.
Усадка повышает сцепление бетона с арматурой, вызывая ее обжатие, что является положительным фактором. Однако неравномерная усадка разных слоев бетона (у поверхности — в большей степени, во внутренних слоях— в меньшей) приводит к наличию «собственных» напряжений (внутренние слои препятствуют свободной усадке поверхностных слоев, в результате чего в последних возникает растяжение) и возникновение усадочных трещин, что нежелательно. Особенно существенно влияние усадки в массивных конструкциях.
Снижение усадки достигается подбором состава бетона (уменьшением объема пор), увлажнением поверхности в период вызревания бетона (особенно в первые дни) и т. п.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 6766; Нарушение авторских прав?; Мы поможем в написании вашей работы!