
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Фотоэлектрический эффект
|
|
|
|
Лекция № 2
Фотоэлектрическим эффектом или фотоэффектом называется испускание электронов веществом под действием света. Это явление было открыто в 1887г. Г.Герцем, который заметил, что проскакивание искры между цинковыми шариками разрядника облегчается, если один из них осветить ультрафиолетовыми лучами.
В 1887г. А.Г.Столетов подверг это явление тщательному изучению и установил, что испускаемые под действием света заряды имеют отрицательный знак. Величина испускаемых зарядов пропорциональна поглощенной световой энергии. Наибольший эффект достигается при действии ультрафиолетовых лучей.
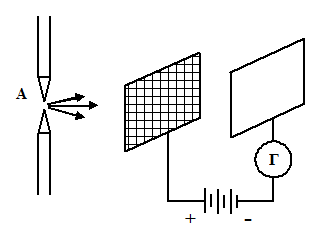 Схема опыта Столетова состояла в следующем: между обкладками кон-денсатора, состоящего из полированной цинковой пластины и металлической сетки, создавалась разность потен-циалов. При освещении цинковой плас-тинки дугой в цепи появлялся электрический ток, величина которого измерялась гальванометром.
Схема опыта Столетова состояла в следующем: между обкладками кон-денсатора, состоящего из полированной цинковой пластины и металлической сетки, создавалась разность потен-циалов. При освещении цинковой плас-тинки дугой в цепи появлялся электрический ток, величина которого измерялась гальванометром.
В 1898г. Ленард и Томсон измерили удельный заряд частиц, вырываемых излучением, и установили, что он равен удельному заряду электронов.
 Вырывание светом электронов из металлов наружу получило название внешнего фотоэффекта. Ток, возникающий при этом, называется фототоком, а электроны, вырванные светом, - фото-электронами.
Вырывание светом электронов из металлов наружу получило название внешнего фотоэффекта. Ток, возникающий при этом, называется фототоком, а электроны, вырванные светом, - фото-электронами.
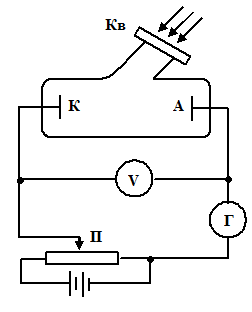
Схема современной установки для иссле-дования фотоэффекта показана на рисунке.
Свет, проникая через кварцевое окошко 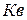 в эвакуированный баллон, освещает катод
в эвакуированный баллон, освещает катод 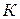 , изготовленный из исследуемого материала. Электроны, вырванные вследствие фотоэффекта, перемещаются под действием электрического поля к аноду
, изготовленный из исследуемого материала. Электроны, вырванные вследствие фотоэффекта, перемещаются под действием электрического поля к аноду 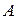 , в результате чего в цепи течет фототок, измеряемый гальванометром
, в результате чего в цепи течет фототок, измеряемый гальванометром 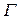 . Напряжение между анодом и катодом можно менять с помощью потенциометра
. Напряжение между анодом и катодом можно менять с помощью потенциометра 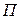 .
.
Усовершенствование методики исследования фотоэффекта было осуществлено П.И. Лукирским и С.С. Прилежаевым, применившим в своей установке метод сферического конденсатора. Анодом в ней служили посеребренные стенки стеклянного сферического баллона. В центре баллона размещается катод в виде шарика.
Полученная в результате экспериментов зависимость силы фототока от разности потенциалов между электродами при неизменном лучистом потоке 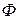 изображена на графике.
изображена на графике.
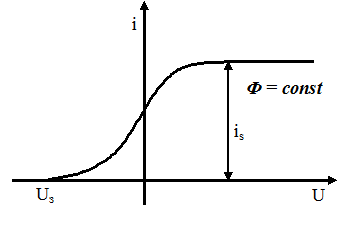 Как видно из графика при некотором значении напряжения сила фототока достигает макси-мального значения и далее остается постоянной.
Как видно из графика при некотором значении напряжения сила фототока достигает макси-мального значения и далее остается постоянной.
Этот ток, называемый током насыщения, соответствует состо-янию, когда все электроны, вырванные из фотокатода, достигают анода. График этот называется вольт-амперной характеристикой.
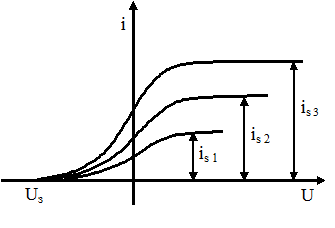 Если изменять значения лучистого потока
Если изменять значения лучистого потока 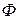 , то получится семейство таких кривых, для данного фотокатода.
, то получится семейство таких кривых, для данного фотокатода.
А.Г.Столетовым был установлен закон, носящий его имя: при неизменном спектральном составе падающего на катод света сила тока насыщения прямо пропор-циональна лучистому потоку
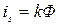 .
.
Как видно из вольт-амперной характеристики при отсутствии напряжения между электродами сила фототока не равна нулю. Это говорит о том, что электроны покидают катод со скоростью отличной от нуля. Для того, чтобы фототок стал равным нулю, нужно приложить задерживающее напряжение 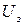 . При таком напряжении ни одному из электронов, даже обладающему при вылете из катода наибольшим значением скорости, не удается преодолеть задерживающее поле и достигнуть анода.
. При таком напряжении ни одному из электронов, даже обладающему при вылете из катода наибольшим значением скорости, не удается преодолеть задерживающее поле и достигнуть анода.
Поэтому можно записать, что
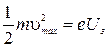 ,
,
где 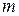 - масса электрона.
- масса электрона.
Из этого соотношения можно определить максимальные значения скорости 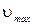 и кинетической энергии фотоэлектронов
и кинетической энергии фотоэлектронов 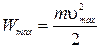 .
.
Как показывает опыт, при освещении катода монохроматическим светом задерживающее напряжение меняется с частотой света по линейному закону
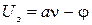 ,
,
где 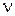 - частота света;
- частота света;
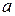 и
и 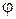 - константы.
- константы.
Умножив это равенство на 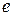 (заряд электрона) и заменив
(заряд электрона) и заменив 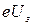 на
на 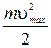 , получим
, получим 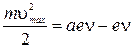 .
.
Отсюда следует, что для того, чтобы электроны могли покинуть катод под действием света, т.е. для того, чтобы 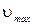 была вещественной, необходимо, чтобы
была вещественной, необходимо, чтобы 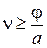 .
.
Обозначив 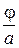 через
через 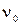 , получим
, получим 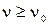 .
.
Частота 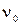 и соответствующая ей длина волны
и соответствующая ей длина волны 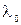 носят название красной границы фотоэффекта или порога фотоэффекта.
носят название красной границы фотоэффекта или порога фотоэффекта.
Таким образом, законами внешнего фотоэффекта можно считать следующие явления:
1. максимальная начальная скорость фотоэлектронов зависит от частоты света и не зависит от его интенсивности;
2. при неизменном спектральном составе падающего на катод света сила тока на насыщения пропорциональна световому потоку;
3. для каждого вещества существует красная граница фотоэффекта, т.е. та минимальная частота, при которой еще возможен фотоэффект;
4. фотоэффект практически безынерционен.
Эти законы фотоэффекта, подтвержденные экспериментально, не удается объяснить, основываясь на волновой теории света.
Согласно представлениям волновой теории, под действием электромагнитной световой волны электроны вещества должны совершать вынужденные колебания с амплитудой пропорциональной амплитуде волны. При достаточной интенсивности колебаний связь электрона с веществом может быть нарушена и электроны будут вылетать наружу со скоростью, величина которой должна зависеть от амплитуды падающего света или его интенсивности. В действительности такой зависимости нет, т.к. скорость электронов зависит только от частоты колебаний.
Кроме того, время, в течение которого электроны под воздействием поля электромагнитной волны накопят энергию, превосходящую работу выхода, согласно волновой теории, должно измеряться несколькими минутами. Следовательно, фотоэффект не может быть безынерционным.
А. Эйнштейн, опираясь на гипотезу Планка о квантах, предложил новое объяснение фотоэлектрических явлений, получившее название квантовой теории фотоэффекта. Он предположил, что свет частоты 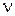 не только излучается, но и распространяется и поглощается отдельными фотонами.
не только излучается, но и распространяется и поглощается отдельными фотонами.
Интенсивность облучения катода определяется числом фотонов, падающих в единицу времени на единицу поверхности катода. Энергия каждого фотона равна
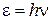 ,
,
где 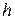 - постоянная Планка;
- постоянная Планка;
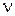 - частота колебаний.
- частота колебаний.
Импульс фотона - 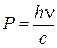 ,
,
где 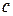 - скорость света в вакууме.
- скорость света в вакууме.
Масса фотона - 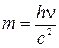 .
.
При падении пучка фотонов на поверхность металла происходит соударение фотонов с электронами, и каждый фотон отдает электрону свою энергию, равную 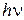 .
.
Для выхода электрона из металла он должен преодолеть потенциальный барьер на границе металл-вакуум и совершить работу выхода 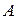 .
.
Если 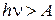 , то электрон может вырваться из металла.
, то электрон может вырваться из металла.
Наибольшую кинетическую энергию, которую сможет приобрести электрон, можно найти по закону сохранения энергии
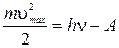 .
.
Это уравнение называется уравнением Эйнштейна для внешнего фотоэффекта.
Как видно из этого уравнения, при частоте света, при которой энергия фотона равна работе выхода, кинетическая энергия электрона равна нулю и фотоэффект наблюдаться не будет. Эта частота и соответствующая ей длина волны и будут красной границей фотоэффекта для данного вещества.
Квантовая теория фотоэффекта позволяет объяснить и закон Столетова. Величина лучистого потока определяется числом фотонов, падающих в единицу времени на поверхность металла. Чем больше это число, тем больше электронов может быть вырвано из металла в единицу времени, следовательно, тем сильнее будет фототок.
Практическая безынерционность фотоэффекта объясняется тем, что передача энергии при столкновении фотонов с электронами происходит почти мгновенно.
Уравнение Эйнштейна для внешнего фотоэффекта можно записать несколько иначе.
Как мы уже знаем, 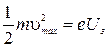 . С учетом этого, уравнение примет вид:
. С учетом этого, уравнение примет вид:
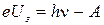 .
.
Расписав в этом выражении 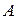 как
как 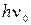 , получим
, получим
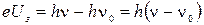 .
.
Подтверждением правильности этой формулы является определение из нее постоянной Планка
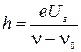 .
.
Производится это следующим образом: из опыта можно определить величину напряжения, при котором исчезает фототок 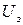 , и построить график зависимости
, и построить график зависимости 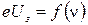 .
.
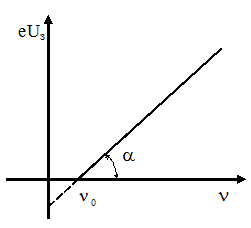 Эта зависимость выражается прямой линией. По углу между искомой прямой и осью абсцисс и можно определить постоянную Планка
Эта зависимость выражается прямой линией. По углу между искомой прямой и осью абсцисс и можно определить постоянную Планка
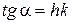 ,
,
где 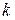 - соотношение размерных величин, принятых за единицы масштаба по осям
- соотношение размерных величин, принятых за единицы масштаба по осям 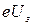 и
и 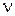 .Полученное таким образом значение
.Полученное таким образом значение 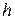 оказалось равным
оказалось равным 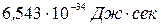 , что хорошо согласуется с результатами других методов определения этой величины. Тем самым подтверждается правильность уравнения Эйнштейна и понятий о квантовом характере взаимодействия света с электронами при фотоэффекте.
, что хорошо согласуется с результатами других методов определения этой величины. Тем самым подтверждается правильность уравнения Эйнштейна и понятий о квантовом характере взаимодействия света с электронами при фотоэффекте.
Технические применения внешнего фотоэффекта основаны на использовании фотоэлементов, в которых электроны под действием света выходят с поверхности катода в вакуум или в разреженный газ. Современные фотоэлементы состоят из фотокатода, являющегося излучателем электронов, и анода, собирающего эти электроны.
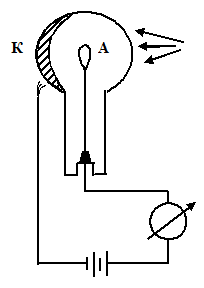 Расположение катода и анода в фотоэлементах показано на схеме.
Расположение катода и анода в фотоэлементах показано на схеме.
Кроме рассмотренного нами внешнего фото-эффекта (называемого обычно фотоэффектом) существует также внутренний фотоэффект, при котором происходит лишь увеличение числа свободных электронов внутри вещества, но не происходит выхода их наружу. Он наблюдается в диэлектриках и полупроводниках.
Внутренний фотоэффект заключается в перераспределении электронов по энергетическим уровням под действием света. Если энергия кванта 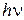 превышает ширину запрещенной зоны полу-проводника, то электрон переходит из валентной зоны в зону проводимости, в результате чего увеличивается электропроводность вещества.
превышает ширину запрещенной зоны полу-проводника, то электрон переходит из валентной зоны в зону проводимости, в результате чего увеличивается электропроводность вещества.
На внутреннем фотоэффекте основано действие фотосопротивлений. Они представляют собой стеклянную пластину, на которую нанесен тонкий слой полупроводника, на поверхности которого укреплены токоподводящие электроды. При освещении фотосопротивления, соединенного с источником напряжения, в цепи появляется электрический ток.
В отличие от фотоэлементов с внешним фотоэффектом фотосопротивления не обладают током насыщения. В них количество образующихся носителей тока пропорционально падающему световому потоку. Поэтому чувствительность фотосопротивлений в сотни и тысячи раз больше чувствительности фотоэлементов с внешним фотоэффектом. Это позволяет использовать фотосопротивления для целей фотометрии.
Возможен и другой вид фотоэффекта – фотогальванический эффект или, как его еще называют, фотоэффект запирающего слоя.
Вводя промежуточный (запирающий) слой с односторонней проводимостью между полупроводником и металлической подложкой, можно фотоэлектроны, освобожденные в полупроводнике под действием света, переводить в металл, откуда они идут во внешнюю цепь и обратно к полупроводнику, без участия какого бы то ни было внешнего источника тока.
В таких фотоэлементах, называемых вентильными или фотоэлементами с запирающим слоем, происходит непосредственное преобразование энергии света в энергию электрического тока. Для них не требуется внешнего источника тока, так как ЭДС появляется в результате действия света.
Фотоэлементы с запирающим слоем нашли широкое применение в создании солнечных батарей, в которых происходит прямое преобразование энергии солнечного излучения в электроэнергию. КПД этих батарей достигает 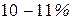 , что составляет около 100 Вт с 1 м2 поверхности при нормально падающем солнечном излучении. Срок службы этих батарей практически неограничен. На советских искусственных спутниках такие фотоэлементы использовались для питания радиоаппаратуры.
, что составляет около 100 Вт с 1 м2 поверхности при нормально падающем солнечном излучении. Срок службы этих батарей практически неограничен. На советских искусственных спутниках такие фотоэлементы использовались для питания радиоаппаратуры.
 Для усиления фототоков используют явление, получившее название вторичной электронной эмиссии. Явление это состоит в том, что при обстреле некоторых веществ быстрыми электронами наблюдается вылет из них новых электронов. При определенных условиях можно добиться того, чтобы каждый падающий электрон выбивал из вещества по нескольку вторичных электронов.
Для усиления фототоков используют явление, получившее название вторичной электронной эмиссии. Явление это состоит в том, что при обстреле некоторых веществ быстрыми электронами наблюдается вылет из них новых электронов. При определенных условиях можно добиться того, чтобы каждый падающий электрон выбивал из вещества по нескольку вторичных электронов.
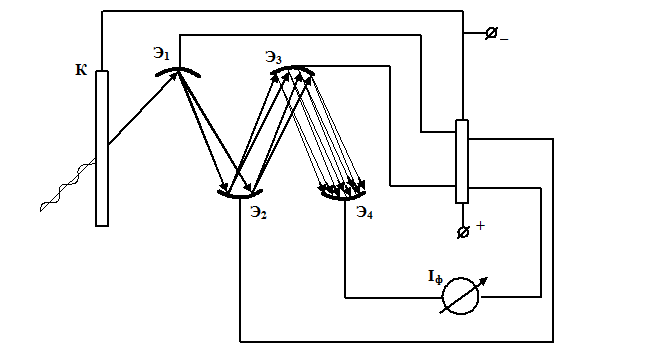
Особенно высокое усиление токов дает прибор, получивший название фотоэлектронного умножителя.
Схема прибора изображена на рисунке.
Фотоэлектроны с катода 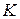 ускоряются в электрическом поле и, попадая на первый эмиттер (излучатель)
ускоряются в электрическом поле и, попадая на первый эмиттер (излучатель) 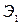 , выбивают из него большее количество электронов. Эти электроны, ускоряясь в свою очередь, попадают на эмиттер
, выбивают из него большее количество электронов. Эти электроны, ускоряясь в свою очередь, попадают на эмиттер 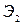 , выбивая из него еще большее количество электронов.
, выбивая из него еще большее количество электронов.
Для того, чтобы электроны следовали по необходимым маршрутам, электродам придают специальную форму и сообщают им нужные потенциалы.
В современных промышленных образцах фотоэлектронного умножителя при девяти ступенях усиления достигается общее усиление фототока в 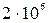 раз при напряжении питания в 1000-1500 вольт. Такой фотоэлектронный умножитель имеет размеры, немного превышающие размера обычной радиолампы.
раз при напряжении питания в 1000-1500 вольт. Такой фотоэлектронный умножитель имеет размеры, немного превышающие размера обычной радиолампы.
На фотоэлектрическом эффекте основаны все современные системы телевидения, т.е. передачи изображений по радио. Для этого необходимо световые сигналы превратить в электрические.
Передаваемое изображение разбивается на элементы, величина которых определяется четкостью изображения. В случае движущегося изображения вся картина передается 25раз в секунду.
Основной частью передающего устройства является мозаика, состоящая из ячеек образованных крупинками серебра, осажденными на слюде.
Вся мозаика располагается на металлической подложке. Поверхность мозаики последовательно, строчка за строчкой, оббегается электронным лучом, при этом ячейки мозаики приобретают положительный потенциал. Если осветить мозаику, спроектировав на нее изображение, то в результате фотоэффекта потенциал ячеек изменится. В зависимости от освещенности ячеек их потенциал будет различным. Таким образом, на поверхности мозаики установится распределение потенциала в соответствии с распределением яркости изображения. При этом соответствующим образом изменится и потенциал металлической подложки. Этот потенциал и используется в качестве видеосигнала.
Далее видеосигнал передается по радио, как и сигнал, получаемый с микрофона при трансляции речи или музыки. В телевизоре электронный луч оббегает поверхность электронно-лучевой трубки, причем принимаемые видеосигналы, поступая на модулирующий электрод, меняют интенсивность этого луча. При этом поверхность трубки светится с большей или меньшей яркостью, воспроизводя изображение.
Световое давление с квантовой точки зрения
Рассмотрим фотон, распространяющийся в вакууме, и применим к нему релятивистскую формулу зависимости массы от скорости
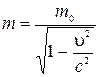 .
.
Для фотона 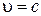 и если считать, что
и если считать, что 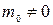 , то эта формула дает бессмысленный результат, т.к.
, то эта формула дает бессмысленный результат, т.к. 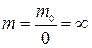 , и, следовательно, энергия фотона
, и, следовательно, энергия фотона 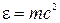 также равна
также равна 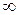 . На самом же деле она равна
. На самом же деле она равна 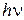 . Следовательно, остается одно
. Следовательно, остается одно 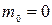 . Это значит, что покоящихся фотонов не существует.
. Это значит, что покоящихся фотонов не существует.
Таким образом, фотон - это особенная частица, существенно отличающаяся от таких частиц, как электрон, протон и нейтрон, которые обладают не равной нулю массой покоя и могут находиться в состоянии покоя.
Фотон не имеет массы покоя и может существовать, только двигаясь со скоростью света.
Кроме энергии и массы фотон обладает импульсом. Связь энергии фотона с его импульсом вытекает из формул теории относительности
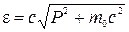 ,
,
где 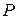 - импульс фотона.
- импульс фотона.
Для фотона 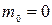 , тогда
, тогда 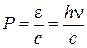 . Эта формула выражает корпускулярные свойства фотона, как частицы света.
. Эта формула выражает корпускулярные свойства фотона, как частицы света.
Эту формулу можно записать несколько иначе, выразив 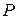 через волновое число
через волновое число 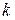 . Под волновым числом в оптике понимают число длин волн, укладывающихся на длине
. Под волновым числом в оптике понимают число длин волн, укладывающихся на длине 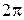 метров, т.е.
метров, т.е.
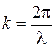 ,
,
где 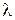 - длина волны.
- длина волны.
Тогда 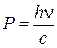 и т.к.
и т.к. 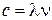 , то
, то 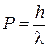 .
.
Выразив в этой формуле 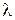 через
через 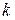 , получим
, получим 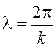 и
и 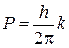 .
.
Обозначив 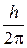 через
через 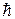 , получим
, получим 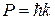 .
.
Введем понятие волнового вектора, который по модулю равен волновому числу 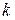 , а по направлению совпадает с направлением распространения света.
, а по направлению совпадает с направлением распространения света.
Тогда искомая формула в векторной форме запишется в виде
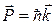 .
.
Эта формула выражает волновые свойства фотона.
Таким образом, на примере рассмотрения импульса фотона мы пронаблюдали связь волновых и корпускулярных свойств света.
Связь эта не случайна. Мы уже отмечали, что свет обнаруживает корпускулярно-волновой дуализм: в одних явлениях проявляется его волновая природа, и он ведет себя, как электромагнитная волна, в других – проявляется корпускулярная природа света, и он ведет себя, как поток фотонов.
Из наличия у фотона импульса вытекает, что свет, падающий на какое-нибудь тело, оказывает на него давление, равное импульсу, сообщаемому фотонами единице поверхности в единицу времени. Мы уже рассматривали световое давление с точки зрения волновой природы света (Ур-ния Максвелла. Плоская эл-магн. волна).
Рассмотрим теперь его с квантовой точки зрения.
Давление света на поверхность тела является результатом того, что при столкновении с поверхностью тела каждый фотон передает ей свой импульс.
Пусть на поверхность тела перпендикулярно к ней падает свет. В единицу времени, на единицу площади падает «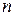 » фотонов. Часть из них поглотится поверхностью и каждый из них передаст ей свой импульс. Часть фотонов отразится. Отраженный фотон полетит в противоположном направлении с импульсом «
» фотонов. Часть из них поглотится поверхностью и каждый из них передаст ей свой импульс. Часть фотонов отразится. Отраженный фотон полетит в противоположном направлении с импульсом «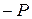 ».
».
Поэтому полный импульс, переданный поверхности отраженным фотоном будет 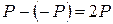 .
.
Давление света на поверхность равно импульсу, который передают в единицу времени все «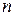 » падающих фотонов.
» падающих фотонов.
Если обозначить через 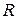 коэффициент отражения света от поверхности, то число отраженных фотонов будет
коэффициент отражения света от поверхности, то число отраженных фотонов будет 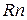 , а число поглощенных фотонов будет
, а число поглощенных фотонов будет 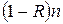 . Таким образом, давление света будет равно
. Таким образом, давление света будет равно
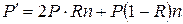 ,
,
где 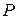 - импульс фотона,
- импульс фотона,
или с учетом того, что 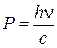 ,
,
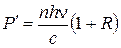 .
.
Произведение 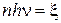 представляет собой энергию всех фотонов, падающих в единицу времени на единицу поверхности. Тогда
представляет собой энергию всех фотонов, падающих в единицу времени на единицу поверхности. Тогда
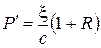 .
.
 Величина
Величина 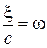 представляет собой объемную плотность энергии падающего света. С учетом этого
представляет собой объемную плотность энергии падающего света. С учетом этого
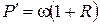 .
.
Эта формула была впервые получена Максвеллом и подтверждена опытами Лебедева. Прибор Лебедева представлял собой очень чувствительные крутильные весы, подвижной частью которых являлась легкая рамка с укрепленными на ней светлыми и черными дисками. Так как давление на черный диск больше, чем давление на светлый диск, то на подвижную систему будет действовать вращающий момент, который можно измерить по углу закручивания нити, на которой подвешена рамка.
На основе ряда наблюдений Лебедев пришел к выводу, что в пределах погрешности эксперимента величина светового давления согласуется с формулой, полученной Максвеллом.
Эффект Комптона
Корпускулярные свойства света особенно отчетливо проявляются в явлении, которое получило название эффекта Комптона.
В 1923г. Комптон, исследуя рассеивание рентгеновских лучей различными веществами, обнаружил, что в рассеянных лучах, наряду с излучением первоначальной длины волны «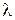 », содержатся также лучи большей длины волны
», содержатся также лучи большей длины волны 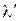 . Им была установлена следующая закономерность
. Им была установлена следующая закономерность
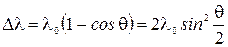 ,
,
где 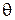 - угол, образованный направлением рассеянного излучения с направлением первичного пучка;
- угол, образованный направлением рассеянного излучения с направлением первичного пучка;
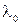 - постоянная величина, равная
- постоянная величина, равная 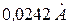 .
.
Схема опыта Комптона изображена ниже.
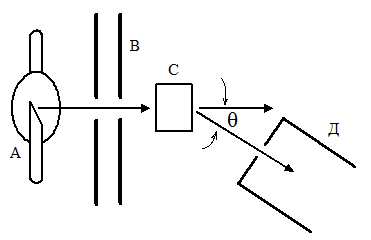 Монохроматические рентгенов-ские лучи, возникшие в рент-геновской трубке
Монохроматические рентгенов-ские лучи, возникшие в рент-геновской трубке 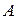 , проходят через диафрагмы
, проходят через диафрагмы 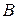 и узким пучком направляются на рассеивающее вещество
и узким пучком направляются на рассеивающее вещество 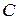 . Рас-сеянные лучи регистрируются рентгеновским спектрографом
. Рас-сеянные лучи регистрируются рентгеновским спектрографом  .
.
Эффект Комптона не объяс-няется волновой теорией, однако его легко объяснить, если рас-сматривать рентгеновские лучи как поток фотонов. При рассеянии их должен выполняться закон сохранения энергии
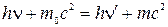 ,
,
где 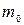 - масса ионов,
- масса ионов, 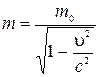 ;
;
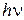 - энергия падающего фотона;
- энергия падающего фотона;
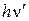 - энергия рассеянного фотона;
- энергия рассеянного фотона;
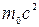 - энергия неподвижного электрона;
- энергия неподвижного электрона;
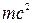 - энергия движущегося электрона.
- энергия движущегося электрона.
Кроме этого должен также выполняться и закон сохранения импульса
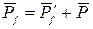 ,
,
где 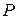 - импульс электрона;
- импульс электрона;
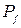 - импульс падающего фотона;
- импульс падающего фотона;
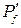 - импульс рассеянного фотона.
- импульс рассеянного фотона.
Это векторные величины. Следовательно, как видно из этого уравнения, они образуют между собой треугольник.
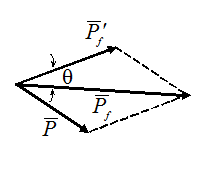 Тогда, согласно теореме косинусов,
Тогда, согласно теореме косинусов,
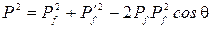 .
.
Так как 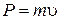 ,
, 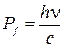 и
и 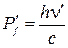 , то
, то
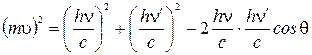 . (1)
. (1)
Разделим уравнение закона сохранения энергии для каждого случая на 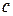 .
.
Тогда 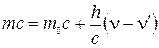 .
.
Возведем его в квадрат
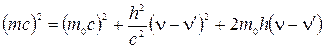
и, расписав второе слагаемое, как
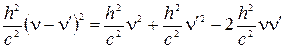 ,
,
получим
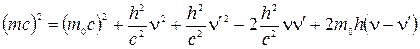 . (2)
. (2)
Вычитая из уравнения (2) уравнение (1), получим
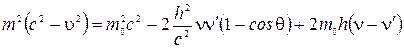 .
.
Так как 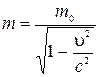 , то
, то 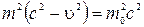 .
.
Подставив это выражение в левую часть предыдущего уравнения, после несложных преобразований получим
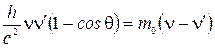 ;
;
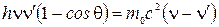 .
.
Разделим полученное равенство на 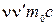 .
.
Тогда 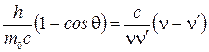 или
или 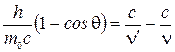 .
.
Так как 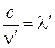 и
и 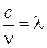 , то равенство примет вид
, то равенство примет вид 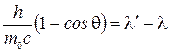 или
или 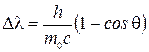 .
.
Обозначив 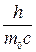 через
через 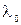 , получим формулу, совпадающую с эмпирической формулой Комптона
, получим формулу, совпадающую с эмпирической формулой Комптона
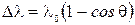 .
.
Как видно из этой формулы, возрастание длины волны рентгеновского излучения при рассеянии фотонов на электронах будет наибольшим при 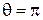 , т.е. при условии, когда фотон после рассеяния полетит назад, в сторону противоположную первоначальному направлению его движения.
, т.е. при условии, когда фотон после рассеяния полетит назад, в сторону противоположную первоначальному направлению его движения.
В этом случае 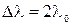 .
.
Формула Комптона показывает также, что изменение длины волны рентгеновского излучения очень мало. Поэтому его можно наблюдать лишь для коротких длин волн, у которых относительное изменение длины волны 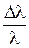 порядка 5%.
порядка 5%.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 10078; Нарушение авторских прав?; Мы поможем в написании вашей работы!