Й учебный вопрос. Построение уравнения двухфакторной линейной регрессии

Уравнение двухфакторной линейной регрессии является простейшим случаем множественной регрессии. На предыдущей лекции мы имели дело с двумя признаками — результативным и факторным.

Но на результат действует обычно не один фактор, а несколько, что необходимо учитывать для достаточно полного анализа связей.

В математической статистике разработаны методы построения множественной регрессии (Регрессия называется множественной, если число независимых переменных, учтенных в ней, больше или равно двум.), Возвратимся к ранее рассмотренному примеру. В нем была определена форма связи между величиной сбора хлеба на душу и размером посева на душу.

Введем в анализ еще один фактор — уровень урожайности (см.табл. 3.1). Без сомнения, эта переменная влияет на сбор хлеба на душу. Но в какой степени влияет? Насколько обе независимые переменные определяют сбор хлеба на душу в черноземных губерниях? Какая из переменных — посев на душу или урожайность — оказывает определяющее влияние на сбор хлеба? Попытаемся ответить на эти вопросы.

После добавления второй независимой переменной уравнение регрессии будет выглядеть так:

y = a₀+a₁x₁+a₂x₂ (3.4)

где у—сбор хлеба на душу; х₁—размер посева на душу; x₂—урожай с десятины (в пудах); а₀, а₁, а₂—параметры, подлежащие определению.

Для нахождения числовых значений искомых параметров, как и в случае одной независимой переменной, пользуются методом наименьших квадратов.

Он сводится к составлению и решению системы нормальных уравнений, которая имеет вид:

Когда система состоит из трех и более нормальных уравнений, решение ее усложняется. Существуют стандартные программы расчета неизвестных параметров регрессионного уравнения на ЭВМ (например, SPCC, Statistica, Statgraphic и другие). При расчете вручную можно воспользоваться известным методом определителей. Использование этого метода чрезвычайно упрощается, если все расчеты вести в программе Excel.

Пример. По данным табл. 3.1 найдем параметры a₀, а₁, а₂.

Построим вспомогательную таблицу 3.2. для составления системы нормальных уравнений:

Таблица 3.2

Вспомогательная таблица для расчета параметров уравнения двухфакторной линейной регрессии

№	y	x1	x2	Х1^2	X2^2	Х1У	УX2	X1Х2
	48,01	0,91	46,08	0,83	2123,37	43,69	2212,30	41,93
	38,18	0,76	45,18	0,58	2041,23	29,02	1724,97	34,34
	38,70	0,82	41,76	0,67	1743,90	31,73	1616,11	34,24
	46,72	0,88	50,94	0,77	2594,88	41,11	2379,92	44,83
	41,58	0,88	43,54	0,77	1895,73	36,59	1810,39	38,32
	36,89	0,89	38,80	0,79	1505,44	32,83	1431,33	34,53
	34,54	0,87	39,22	0,76	1538,21	30,05	1354,66	34,12
	42,86	0,94	42,74	0,88	1826,71	40,29	1831,84	40,18
	38,97	0,91	41,20	0,83	1697,44	35,46	1605,56	37,49
	43,22	1,07	39,35	1,14	1548,42	46,25	1700,71	42,10
	28,19	0,69	34,38	0,48	1181,98	19,45	969,17	23,72
	38,65	0,74	48,98	0,55	2399,04	28,60	1893,08	36,25
	36,26	0,90	40,06	0,81	1604,80	32,63	1452,58	36,05
	32,07	0,52	57,91	0,27	3353,57	16,68	1857,17	30,11
	32,83	0,66	43,86	0,44	1923,70	21,67	1439,92	28,95
	35,16	0,58	58,62	0,34	3436,30	20,39	2061,08	34,00
	44,56	0,99	44,39	0,98	1970,47	44,11	1978,02	43,95
	59,16	1,63	35,77	2,66	1279,49	96,43	2116,15	58,31
	67,99	1,95	35,96	3,80	1293,12	132,58	2444,92	70,12
	53,73	1,27	40,99	1,61	1680,18	68,24	2202,39	52,06
	52,39	1,55	33,05	2,40	1092,30	81,20	1731,49	51,23
	36,10	1,15	30,68	1,32	941,26	41,52	1107,55	35,28
	32,67	0,94	34,26	0,88	1173,75	30,71	1119,27	32,20
Σ	959,43	22,50	967,72	16,06	22148,00	614,76	21403,63	508,50

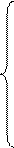Используя суммы, рассчитанные в последней строке таблицы 3.2, построим систему нормальных уравнений и решим ее.

23a₀ + 22,5a₁+967,72a₂ = 959,43

22,5a₀+16,06a₁+508,5a₃=614,76 (3.5)

967,72 a₀+508,50a₁+22148a₃=21403,63

Решая систему (3.5) методом определителей, получаем следующие результаты: a₀ = -0,85, a₁ =28,18, a₂ =0,36.

Таким образом, уравнение множественной регрессии между величиной сбора хлеба на душу населения (у), размером посева на душу (x₁) и уровнем урожайности (х₂) имеет вид:

у = -0,85+28,18x₁+0,36x₂ (3.6)

Дата добавления: 2014-01-05