
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Введение. Тема лекции:«Линеаризация нелинейных уравнений регрессии»
|
|
|
|
ТЕКСТ ЛЕКЦИИ
Тема лекции: «Линеаризация нелинейных уравнений регрессии»
Учебные и воспитательные цели:
1. Ознакомление студентов с различными видами нелинейных уравнений регрессии и способами их приведения к линейному виду
2. Усвоение возможности и причин нарушения теоретических предпосылок МНК при использовании метода для построения нелинейных уравнений регрессии
3. Изучение основных способов проверки предпосылок о характере поведения остатков уравнения регрессии
Время: 2 часа (90 мин.).
Литература (основная):
1. «Эконометрика», под редакцией Елисеевой И.И., М., «Финансы и статистика», 2005г
2.Елисеева И.И., Курышева С.В., Гордеенко Н.М., Бабаева И.В., Костеева Т.В., Михайлов Б.А., «Практикум по эконометрике», Изд-во «Финансы и статистика», Москва, 2004.
Литература (дополнительная):
4. Доугерти К., «Введение в эконометрику», Инфра-М, Москва, 2004.
5. Тихомиров Н.П., Дорохина Е.Ю., «Учебно-методическое пособие по дисциплине «Эконометрика», Изд-во РЭА., Москва, 2004.
6. Кремер Н.Ш., Путко Б.А., «Эконометрика: Учебник для вузов», ЮНИТИ-ДАНА, Москва, 2004.
Учебно-материальное обеспечение:
Наглядные пособия: раздаточный материал в виде плакатов
Технические средства обучения: электронный конспект лекций
ПЛАН ЛЕКЦИИ:
Введение – до 5 мин.
Основная часть (учебные вопросы) – до 80 мин.
1-й учебный вопрос: Понятие линеаризации и основные типы уравнений нелинейной регрессии - 30 мин.
2-й учебный вопрос: Построение систем нормальных уравнений для нелинейных уравнений регрессии – 20 мин.
3-й учебный вопрос: Способы проверки предпосылок МНК – 30 мин.
Заключение – до 5 мин.
До сих пор мы, в основном, изучали линейные уравнения парной и множественной регрессии. Но не всегда связь между признаками может быть достаточно хорошо представлена линейной функцией. Иногда для описания реально существующей статистической зависимости более пригодными, а порой и единственно возможными являются более сложные нелинейные функции. Метод наименьших квадратов, как мы заметили, изучая его сущность, был разработан для линейных функций. Его использование для расчета параметров нелинейных уравнений регрессии, основано на предварительном приведении нелинейных уравнений к линейному виду, то есть на процедуре их линеаризации. На данной лекции мы рассмотрим различные виды уравнений нелинейной регрессии, способы их приведения к линейному виду, и различные проблемы, возникающие в связи с этим.
1-й учебный вопрос: Понятие линеаризации и основные типы уравнений нелинейной регрессии
Как уже отмечалось, метод наименьших квадратов (МНК) был разработан для расчета параметров уравнений линейной регрессии, но многие соотношения между экономическими показателями очень часто приходится оценивать с помощью нелинейной функции (параболы, гиперболы).
Для того, чтобы привести нелинейные уравнения регрессии к линейному виду используются различные специальные процедуры, совокупность которых называются линеаризацией.
Таким образом, линеаризация уравнений регрессии – это использование различных процедур (логарифмирование, замена переменных), в результате которых нелинейные уравнения приводятся к линейному виду. Следует учитывать, что далеко не все нелинейные уравнения легко привести к линейному виду.
Поэтому в эконометрике принято различные нелинейные уравнения регрессии делить на несколько типов, в зависимости от того, насколько сложной является процедура их линеаризации.
Прежде всего, различают два класса нелинейных уравнений регрессии.
Первый класс – это уравнения регрессии, нелинейные относительно факторных переменных (x1,x2), но линейные относительно параметров (a0,a1,a2…).
К этому классу относятся, например, следующие уравнения:
y=a0 + a1x + a2x2(парабола)
y= a0 + a1x + a2x2 + a3x3 + …+ anxn (полином n–ой степени)
y= a0 + a1/x (гипербола)
Второй класс – это уравнения, нелинейные относительно оцениваемых параметров.
К этому классу относятся, например, следующие уравнения:
y=a0 xa1 (степенная)
y=a0 a1x (показательная)
y=ea0+a1*x(экспоненциальная)
Кроме того, к данному классу относятся так называемые функции с пределом насыщения или S -образные кривые: например, логистическая функция
y = 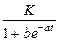 ;
;
логистическая кривая Перла-Рида
y =  ;
;
кривая Гомперца
y = 
и некоторые другие).
Далее мы рассмотрим более подробно различные способы линеаризации описанных функций и построение систем нормальных уравнений для каждой из них.
Построение систем нормальных уравнений для расчета параметров нелинейных уравнений регрессии
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 913; Нарушение авторских прав?; Мы поможем в написании вашей работы!