Демультиплексор

Иногда возникает обратная задача – передача одного входного сигнала по нескольким различным адресам. Схемное решение такой задачи приведено на рис.5. На рисунке приведена схема демультиплексора на 4 выхода. Если схема имеет n адресных входов, то она может управлять 2ⁿ выходами.

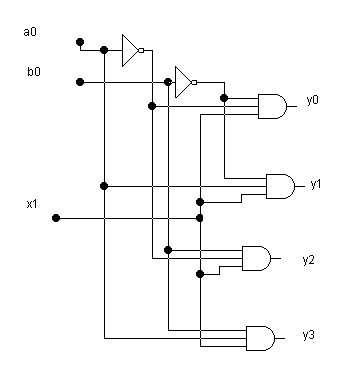
Рис.5.

Промышленностью выпускаются следующие демультиплексоры в интегральном исполнении:

	TTL	ЭСЛ	КМОП
16 выходов	SN 74154		МС 14514
10 выходов	SN 7442
8 выхода	SN 74S138	МС 10162
2х4 выхода	SN 74155	МС 10172	МС14555

Если на х подавать логическую 1, то демультиплексор работает как дешифратор. Вход х можно рассматривать как стробирующий вход такого дешифратора.

Кроме функции коммутации входов мультиплексор позволяет реализовать множество ФАЛ.

Пусть ФАЛ задана картой Карно:

x2x3
x1

Запишем ФАЛ

_ _ _ _ _ _

Y = x₁x₂x₃ + x₁x₂x₃ + x₁x₂x₃ + x₁x₂x₃

Сравним ее с формулой мультиплексора для 3-х переменных:

_ _ _ _ _ _ _ _ _ _ _

Y = A₀A₁A₂D₀ + A₀A₁A₂D₁ + A₀A₁A₂D₂ + A₀A₁A₂D₃ + A₀A₁A₂D₄ + A₀A₁A₂D₅ +

_

+ A₀A₁A₂D₆ + A₀A₁A₂D₇

Из сравнения получим значения коэффициентов D_i:

D₀ = D₃ = D₅ = D₆ = 1

D₁ = D₂ = D₄ = D₇ = 0

Тогда для реализации ФАЛ необходимо на адресные входы A_0, A_1, A₂ подать переменные x_1, x_2, x₃ а на информационные входы D₀ – D₇ подать 0 или 1 в соответствии с их значениями.

0 1

D₀

D₁ К8-1

D₂

D₃

D₄

D₅ Y

D₆

D₇

X₀ A₀

X₁ A₁

X₂ A₂

Мы рассмотрели простой случай, когда количество переменных равно количеству адресных входов.

Возможно построение ФАЛ на мультиплексоре даже если количество переменных превышает количество адресных входов.

В общем случае, когда требуется синтезировать КУ, реализующее функцию N аргументов на мультиплексоре с M управляющими входами и 2^М информационными входами, М младших переменных из набора Х₁, Х_2, .... Х_N следует подать на управляющие входы, а информационные сигналы (настроечные) D₀, D₁,.... D₂^м нужно представить функциями остальных (N - M) переменных, как показано на рис. Тогда синтез КУ сводится, по сути дела, к синтезу схемы формирования информационных сигналов, которую можно рассматривать как внутреннее более простое КУ.

X_m+1 D₀

К8-1

Схема

формиро-

вания

КУ Y

X_N

D₂^m

X₀ A₀

X_m A_m

Например, пусть требуется реализовать на мультиплексоре с 2-мя адресными входами (4 информационных) ФАЛ 3-х переменных:

_ _ _ _ _ _

Y = x₁x₂x₃ + x₁x₂x₃ + x₁x₂x₃ + x₁x₂x₃

Воспользуемся методом декомпозиции и представим ФАЛ в виде функции двух переменных, и функции на множестве 0,1, третья переменная.

_ _ _ _

Y = f₀(0,0,x₃) x₁x₂ + f₁(0,1,x₃) x₁x₂ + f₂(1,0,x₃) x₁x₂ + f₃(1,1,) x₁x₂

Вычислим f_i

_ _

f₀ = x₃, f₁ = x₃, f₂ = x₃, f₃ = x₃

Подаем на управляющие входы х0, х1 а на информационные входы D0-D3 подадим вычисленные значения f_i.

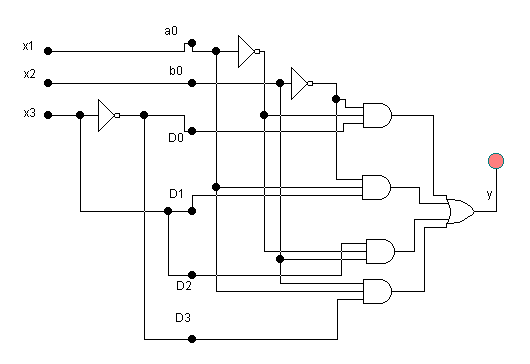
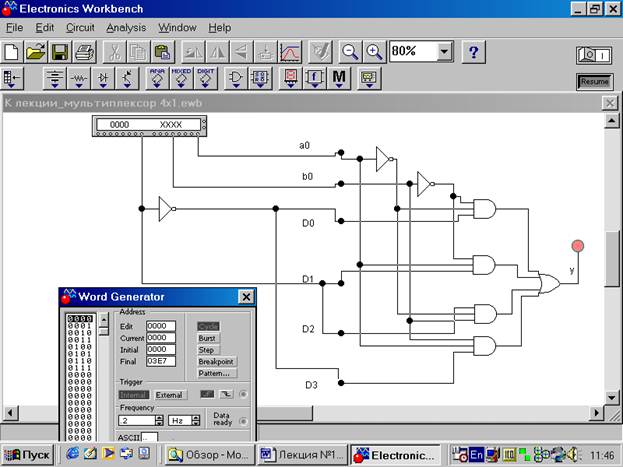
Например, пусть требуется реализовать на мультиплексоре с 3-мя адресными входами (8 информационных) ФАЛ 4-х переменных:

_ _ _ _ _ _ _ _

Y = x₁x₂x₃ + x₁x₂x₃ + x₂x₃x₄ + x₂x₃x₄ + x₁x₃x₄ + x₁x₂x₄

Воспользуемся методом декомпозиции и представим ФАЛ в виде функции трех переменных, и функции на множестве 0,1, четвертая переменная. _ _ _ _ _ _ _

Y = f₀(0,0,0,x₄) x₁x₂x₃ + f₁(0,0,1,x₄) x₁x₂x₃ + f₂(0,1,0,x₄) x₁x₂x₃ +

_ _ _ _

f₃(0,1,1,x₄) x₁x₂x₃ + f₄(1,0,0,x₄) x₁x₂x₃ + f₅(1,0,1,x₄) x₁x₂x₃ +

_

f₆(1,1,0,x₄) x₁x₂x₃ + f₇(1,1,1,x₄) x₁x₂x₃

Вычислим f_i

_ _

f₀ = 0, f₁ = x₄, f₂ = 1, f₃ = 0, f₄ = x₄, f₅ = 1, f₆ = 1, f₇ = x₄

Таким образом, для реализации заданной ФАЛ необходимо на 3 адресных входа подать переменные x_1, x_2, x₃, а на каждый из 8-ми информационных входов – соответствующее значение f_i.

0 1

D₀

D₁ К8-1

^· D₂

D₃

X₄ D₄

^· D₅ Y

_ D₆

X₄ ^`· D₇

X₀ A₀

X₁ A₁

X₂ A₂

Дата добавления: 2014-01-05