И 2 не подходят для оптимизации

Метод Ньютона.

1. - один постоянный член любой точки данной функции является оптимальным – тривиальный случай;
2. линейная функция (двучлен)

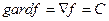(возможно бесконечное уменьшение и увеличение)

1. трехчлен

;

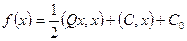без ограничения общности можно положить что матрица q – симметричная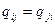

Разложим функцию в ряд Тейлора (должно быть 3 члена). Чтобы найти линейный член квадратичной функции, надо взять grad.

;

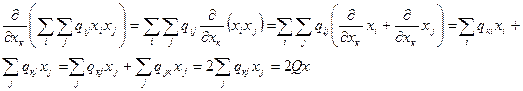
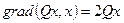; С = 0

Найдем матрицу Гесса (матрица вторых частных производных)

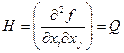
элемент матрицы Гесса является элементом функции Q. 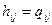(все частные производные высших порядков равны 0).

Функция экстремальна, если grad в данной точке равен 0, следовательно условие экстремальности - система.

Необходимое условие оптимальности:

Если 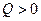решение данной системы существует и оно единственное (совместная система).

Если 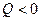решение данной системы существует и оно единственное, т.е. если Q знакоопределена, то существует решение и оно единственное.

Если имеем квадратичную функцию и матрица положительно определена, то линии уровня – эллипсы.

Собственные значения определяют оси эллипсов.

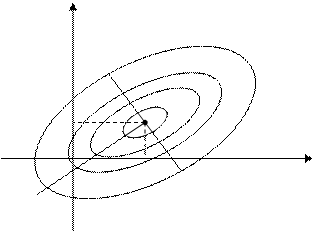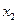
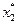
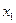
Чтобы определить координаты точки локального минимума, нужно решить систему .

Пусть f(x) – произвольная функция и надо найти точку локального минимума. Разложим функцию в ряд Тейлора в окрестности точки.

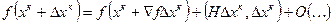
Пусть функция не квадратичная, эллипсы примерно отражают кривизну линий уровня и находятся в окрестности точки 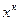. В окрестности точки 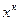находим приближение и заменяем эту функцию квадратичной функцией, которая получается из разложения в ряд Тейлора. Далее решаем задачу минимизации.

Находим точку минимума и рассматриваем эту точку как следующее приближение и т.д.

Для нахождения точки минимума квадратичной функции (зависит от 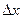)необходимо решить систему:

Окончательно следующее приближение .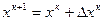

- формула Ньютона

(обобщение формулы минимизации одной переменной)

Выполнение метода останавливается когда , т.е. когда 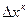очень мало. Для получения практической точности достаточно выполнить 4 итерации метода Ньютона.

Если f – хороша, то метод Ньютона подходит, если f – квадратичная функция, то метод Ньютона приводит к минимальной точке за 1 шаг, из любой точки.

Недостатки:

1. на каждом шаге итерации надо находить решение системы ;
2. С ростом числа итераций Н – разрежается, т.е. большое число членов становится равными 0.

Все формулы безусловной минимизации можно записать в общую схему:

1. выбор направления;
2. выбор шага.

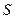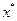
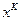
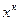- приближение в точке локального минимума, чтобы приблизиться к искомой точке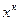. Мы должны выбрать направление, в конце получим локальную линию.

Допустим, требуется f(x)àmin; - начальное приближение; 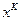- текущее приближение

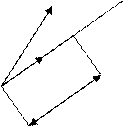
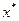
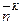
а) выбор направления ;

б) движение вдоль выбранного направления

Задачи оптимизации с ограничениями – разностями (ЗОР)

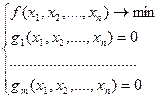
Пример:

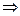
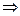
Функции заданы аналитическим выражением можно разрешить относительно одной из переменных 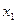можно исключить из f и 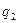, подставив вместо нее :

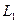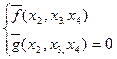
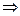
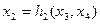
Тогда, - задача безусловной оптимизации. Находим вычисляем

Дата добавления: 2014-01-05