Задачи линейного программирования (ЛП)

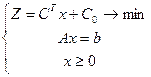
- стандартная форма задачи ЛП

В общем случае, если , то допустимая область представляющая собой многогранник в пространстве.

В случае 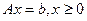- многогранник, имеющий неполную размерность.

Допустим, имеется некоторое выпуклое множество. Тогда в любой граничной точке этого множества, всегда можно провести опорную гиперплоскость, т.е. такую гиперплоскость которая имеет с множеством только одну общую точку, и все множество находится по одну сторону от гиперплоскости.

Если –grad является нормалью к гиперплоскости и плоскость не опорная, то можно двигаться под острым углом к –grad, тем самым улучшая значение функции. Такое движение невозможно, если антиградиент определяет опорную плоскость. Следовательно в этом случае это точка локального минимума, который является и глобальным.

Геометрически, чтобы найти точку локального минимума, необходимо найти такую вершину глобального множества, что плоскость которая является нормальной к антиградиенту является опорной.

Рассмотрим 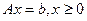, т – ограничений равенств, п – число переменных.

n

m A

Первые m столбцов линейно независимы. , .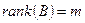

n n-m

A = B N m

Базисная матрица

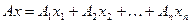, - столбцы матрицы

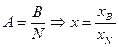- базисные переменные

Тогда систему ограничений равенств можно записать

;

;

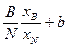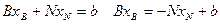Для В существует обратная матрица ;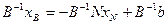

Если для данного базиса зафиксируем не базисные переменные в нуле, то получим точку, которая является вершиной многогранника.

Вершины многогранника множества характеризуемые тем, что небазисные переменные равны 0.

Что делать если вершина не точка оптимума.

Рассмотрим целевую функцию:

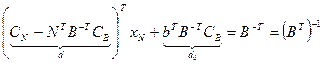
d – показывает суммарное влияние небазисных переменных на целевую функцию

d₀ – множители Лагранжа или относительные оценки небазисных переменных.

Z

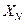
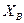
Точка будет точкой оптимума, если все .

Если имеется один отрицательный коэффициент.

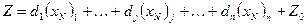
следовательно можно увеличить 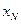, тогда целевая функция начнет улучшаться.

, если 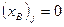, то дальше 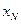увеличивать нельзя 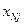и меняются местами.

Дата добавления: 2014-01-05