
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Распределительный метод решения транспортной задачи
|
|
|
|
Пример 7. Найти оптимальное распределение поставок в задаче 1.
Решение. Начнем с базисного распределения поставок, полученного в задаче 3. Как было установлено ранее (см. задачу 5), данное распределение не оптимально. Оценки свободных клеток приведены в (13).
Далее поступаем так, как поступили бы при решении задачи симплекс- методом: переменную  , например, коэффициент при которой отрицателен, будем переводить в базисные (основные) переменные. Переменная
, например, коэффициент при которой отрицателен, будем переводить в базисные (основные) переменные. Переменная  начинает возрастать от нуля. Как было показано в примере 3, перевод поставки в свободную клетку вызывает перераспределение поставок (передвижение поставки по циклу). Означенный цикл пересчета для клетки (1,3) показан на рис. 3.
начинает возрастать от нуля. Как было показано в примере 3, перевод поставки в свободную клетку вызывает перераспределение поставок (передвижение поставки по циклу). Означенный цикл пересчета для клетки (1,3) показан на рис. 3.

Рис. 3
Подобно тому, как это было в симплекс-методе, увеличиваем поставку  в клетке (1,3) до тех пор, пока поставка в одной заполненных клеток не станет равной нулю (дальнейшее увеличение
в клетке (1,3) до тех пор, пока поставка в одной заполненных клеток не станет равной нулю (дальнейшее увеличение  приводит в область недопустимых решений). Эта клетка принадлежит, конечно, циклу, построенному на рис. 3 для клетки (1,3).
приводит в область недопустимых решений). Эта клетка принадлежит, конечно, циклу, построенному на рис. 3 для клетки (1,3).
Найдем ее. Если в клетку (1,3) передать поставку, равную  , то поставка в клетках цикла со знаком "+" увеличится на z, а в клетках со знаком "-" - уменьшится на z. Поэтому искомая клетка находится среди клеток цикла, имеющих знак «-» Более того, она имеет минимальную поставку среди таких клеток. Так как min{60,40} = 40 (рис. 3), то в нашем случае - это клетка (3,3), и для обнуления поставки в этой клетке по циклу следует передать 40 единиц груза. Таким образом, поставка, передаваемая по циклу, определяется как минимум среди поставок в клетках цикла со зна ком «-». После этого клетка (1,3) считается заполненной, а клетка (3,3) — свободной.
, то поставка в клетках цикла со знаком "+" увеличится на z, а в клетках со знаком "-" - уменьшится на z. Поэтому искомая клетка находится среди клеток цикла, имеющих знак «-» Более того, она имеет минимальную поставку среди таких клеток. Так как min{60,40} = 40 (рис. 3), то в нашем случае - это клетка (3,3), и для обнуления поставки в этой клетке по циклу следует передать 40 единиц груза. Таким образом, поставка, передаваемая по циклу, определяется как минимум среди поставок в клетках цикла со зна ком «-». После этого клетка (1,3) считается заполненной, а клетка (3,3) — свободной.
В клетках со знаком "+" цикла поставка увеличивается на передаваемую поставку: поставка клетки (3,2) станет равной 90 единицам, поставка клетки (1,3) - 40 единицам. Аналогично в клетках со знаком " - " поставка уменьшится на передаваемую поставку, например, поставка клетки (1,2) станет равной 20 единицам, что видно из табл. 12. Нетрудно доказать, что вновь полученное распределение поставок - базисное.
И вновь возникает вопрос об оптимальности базисного распределения поставок - круг решения замкнулся.
Найдем оценки свободных клеток (матрицу оценок) распределения поставок. Для этого, как и прежде, подберем потенциалы так, чтобы коэффициенты затрат заполненных клеток стали равными нулю (табл.12). Тогда матрица оценок примет вид (10).
Табл.12
| 20 | |||
|
-2
-1
-3
0 0 -3 -1
Так как среди свободных клеток есть клетка (1,1) с отрицательной оценкой, то найденное распределение не оптимально и передача поставки в клетку (1,1) ведет к уменьшению суммарных затрат на перевозку. Означенный цикл пересчета для клетки (1,1) приведен на рис. 4. По правилу, сформулированному выше, поставка, передаваемая по циклу  = {20, 20, 10}= = 10. Передвигая эту поставку по циклу (рис. 4), приходим к новому распределению поставок (табл. 13).
= {20, 20, 10}= = 10. Передвигая эту поставку по циклу (рис. 4), приходим к новому распределению поставок (табл. 13).
Найдя матрицу (11) оценок этого распределения, заключаем, что оно оптимально, так как среди оценок свободных клеток нет отрицательных.
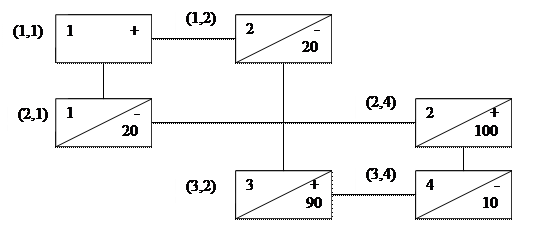
Рис. 4
Табл. 13
|
Суммарные затраты на перевозку этого распределения поставок в денежных единицах составляют:
Fmin = 1*10 +2*10 +5*40+1*10 +2*110 + 3*100 = 760.
Экономия 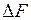 , достигнутая в результате применения метода перераспределения поставок, составляет в денежных единицах
, достигнутая в результате применения метода перераспределения поставок, составляет в денежных единицах  . Знак " - " в данном случае показывает, что при переходе к оптимальному распределению суммарные затраты на перевозку уменьшились.
. Знак " - " в данном случае показывает, что при переходе к оптимальному распределению суммарные затраты на перевозку уменьшились.
Замечание 1. Поставка, передаваемая по циклу, не может быть ни меньше, ни больше минимума поставок клеток цикла со знаком " - ". Действительно, в первом случае ни одна из клеток цикла не будет иметь нулевой поставки, а потому общее число заполненных клеток таблицы будет равно 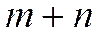 и, следовательно, распределение не будет базисным. Во втором случае уходим в область недопустимых решений.
и, следовательно, распределение не будет базисным. Во втором случае уходим в область недопустимых решений.
Замечание 2. Оптимальное распределение поставок, найденное в задаче 7 (табл.13), не единственное, так как среди оценок свободных клеток есть нулевые, например клетка (2,3) в матрице (11).
Замечание 3. В некоторых случаях требуется определить изменение затрат 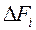 на перевозку (экономию затрат) для некоторого i-го шага решения (или для каждого из шагов) транспортной задачи.
на перевозку (экономию затрат) для некоторого i-го шага решения (или для каждого из шагов) транспортной задачи.
Из экономического смысла оценки свободной клетки следует, что экономия затрат 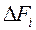 , достигнутая на некотором i -м шаге, равна произведению оценки клетки, в которую передается поставка, на передаваемую поставку. Например, при переходе от исходного распределения поставок (табл. 11) к распределению поставок по табл. 12 поставка в 40 единиц передается в клетку, оценка которой равна -1. Тогда экономия затрат
, достигнутая на некотором i -м шаге, равна произведению оценки клетки, в которую передается поставка, на передаваемую поставку. Например, при переходе от исходного распределения поставок (табл. 11) к распределению поставок по табл. 12 поставка в 40 единиц передается в клетку, оценка которой равна -1. Тогда экономия затрат 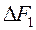 на первом шаге задачи 7 составит
на первом шаге задачи 7 составит
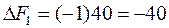 .
.
Последовательность действий по решению произвольной закрытой транспортной задачи теперь может быть изложена в виде следующего алгоритма.
1. Для данного базисного распределения поставок подбираем потенциалы строк и столбцов таблицы поставок так, чтобы коэффициенты затрат заполненных клеток стали равны нулю. Составляем матрицу оценок.
2. Если оценки всех свободных клеток неотрицательны, то найденное распределение оптимально — решение закончено. Если среди оценок свободных клеток есть отрицательные, то выбираем одну из них для передачи в нее поставки (для определенности можно брать, например, одну из клеток с наименьшей оценкой).
3. Для избранной свободной. клетки строится означенный цикл пересчета. Поставка z, передаваемая по циклу, определяется как минимум среди поставок в клетках со знаком " - ". Найденная поставка передвигается по циклу. При этом поставка в клетках цикла со знаком "+" увеличивается на z, а в клетках со знаком " - " уменьшается на z. Клетка, поставка в которой при этом станет равной нулю, будет считаться свободной (далее рассмотрен случай, когда таких клеток несколько), остальные клетки цикла — заполненными. Таким образом, получено новое базисное распределение поставок.
4. Переходим к п. 1 алгоритма.
Рассмотрим особые случаи, которые могут возникнуть при решении транспортной задачи.
1. В некоторых случаях поставка, переводимая по циклу, может оказаться равной нулю. Это возможно тогда, когда клетка цикла со знаком "-" содержала нулевую поставку. В этом случае по циклу передается нулевая поставка. В результате та свободная клетка, для которой был построен цикл, становится заполненной (нулевой поставкой), а клетка с нулевой поставкой — свободной.
2. Если при переводе поставки по циклу поставка обращается в нуль сразу в нескольких заполненных клетках, то свободной из них следует считать только одну (любую), остальные клетки, поставка в которых стала равной нулю, следует считать заполненными нулевой поставкой. Разберем перечисленные особые случаи на примере.
Пример 8. Завершить решение транспортной задачи из примера 4.
Решение. Установим сначала, оптимально ли распределение поставок, полученное в указанном примере методом "северо-западного" угла (табл. 8). Подберем потенциалы строк и столбцов этой таблицы поставок так, чтобы коэффициенты затрат заполненных клеток стали равны нулю (табл. 14).
Табл. 14
|
-1 -3 -2
Это приводит к матрице оценок (12). Так как среди свободных клеток таблицы есть клетка (3,2) с отрицательной оценкой, то данное базисное распределение поставок не оптимально. Переведем поставку в клетку (3,2) с отрицательной оценкой. Строя для клетки (3,2) означенный цикл пересчета (рис. 5), находим, что объем передаваемой поставки в данном случае равен х 32 =min{0,10}= 0. Передавая по построенному циклу нулевую поставку, приходим к новому базисному распределению (табл. 15).

Рис. 5
Табл. 15
|
-2
1 -1 -2
Подбирая потенциалы к строкам и столбцам табл. 15, находим матрицу (13) оценок данного распределения. Так как среди свободных клеток таблицы есть клетка (1,3) с отрицательной оценкой, то данное базисное распределение не оптимально. Найдем новое базисное распределение, передавая поставку в клетку (1,3) с отрицательной оценкой. Построим цикл для клетки (1,3), показанный на рис. 6.
Поставка, передаваемая в клетку (1,3): 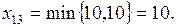 При передаче по циклу (рис. 6) 10 единиц груза станут равными нулю поставки в клетках (1,2) и (3,3). Полагаем, что только одна из них стала свободной, например клетка (3,3), а клетка (1,2) заполнена нулевой поставкой. Таким образом, будет получено базисное распределение поставок, представленное в табл. 16.
При передаче по циклу (рис. 6) 10 единиц груза станут равными нулю поставки в клетках (1,2) и (3,3). Полагаем, что только одна из них стала свободной, например клетка (3,3), а клетка (1,2) заполнена нулевой поставкой. Таким образом, будет получено базисное распределение поставок, представленное в табл. 16.
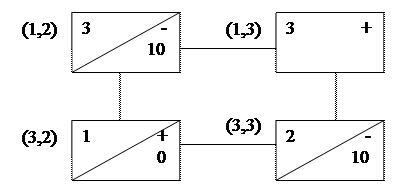
Рис. 6
Табл. 16
|
-1
0 -2 -2
Определяя матрицу оценок (14), видим, что среди оценок свободных клеток найденного распределения нет отрицательных, т.е. найденное распределение (табл. 16) оптимально.
Открытая модель транспортной задачи
Открытая транспортная задача решается сведением ее к закрытой транспортной задаче.
Пример 9. Найти оптимальное распределение поставок для транспортной задачи (табл. 17).
Табл. 17 Табл. 18
Решение. В данном случае суммарный спрос потребителей больше, чем суммарное предложение поставщиков (45+35+55+ +65 = 200 > 40+60+90 = 190). Введем "фиктивного поставщика" и в таблицу поставок добавим дополнительную строку (табл. 18) так, чтобы задача стала закрытой. Для этого мощность фиктивного поставщика следует принять равной 10 = 200—190. Коэффициенты затрат этой добавленной строки определяются издержками ввиду недогрузки мощностей потребителей. Если информация об этих издержках отсутствует, то их принимают равными одному и тому же числу (например, нулю, как в табл. 18). Согласно теореме 3, конкретное значение этого числа не влияет на оптимальное распределение поставок.
Первоначальное распределение поставок для сформулированной закрытой транспортной задачи найдем, например, по методу наименьших затрат. Для удобства укажем последовательность заполнения таблицы поставок:  . В результате приходим к следующему базисному распределению поставок (табл. 19).
. В результате приходим к следующему базисному распределению поставок (табл. 19).
Табл.19
|
-2
-3
-4
-2
0 1 0 2
Установим, оптимально ли это распределение - найдем для него матрицу оценок (15). Так как среди оценок свободных клеток есть отрицательные, то найденное распределение не оптимально. Переведем поставку в одну из клеток с наименьшей отрицательной оценкой, например в клетку (4,3). Цикл для этой клетки изображен на рис 7. Поставка, передаваемая по циклу, равна х43 = min {50, 35, 10} = 10. Передвигая по циклу поставку, равную 10 единицам, приходим к следующему распределению поставок (табл. 20).
Найдем оценки свободных клеток данного распределения (20). Так как оценки всех свободных клеток неотрицательны, то распределение поставок табл. 20 оптимальное.
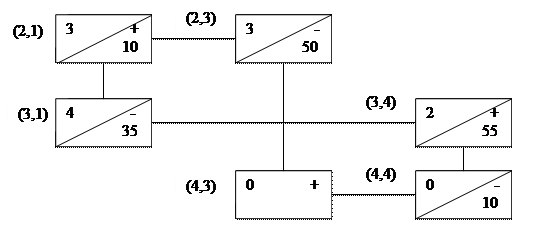
Рис. 7
Табл. 20
|
В случае, когда суммарная мощность поставщиков больше суммарной мощности потребителей, в рассмотрение вводится "фиктивный потребитель", а к таблице поставок присоединяется дополнительный столбец. Коэффициенты затрат этого добавленного столбца соответствуют затратам на хранение неотправленного груза (поставки последнего столбца – неотправленный груз для каждого из поставщиков). Если информация об этих затратах отсутствует, то их принимают равными какому-либо значению (например, нулю).
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 2068; Нарушение авторских прав?; Мы поможем в написании вашей работы!
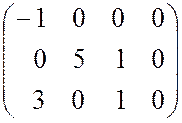 . (10)
. (10)
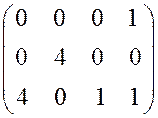 . (11)
. (11)
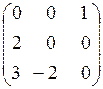 . (12)
. (12)
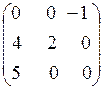 . (13)
. (13)
 . (14)
. (14)
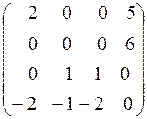 . (15)
. (15)
 . (16)
. (16)