
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Проверка опорного плана на оптимальность
|
|
|
|
Запишем исходную модель КТЗ в векторной форме:
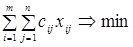 (5)
(5)
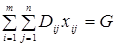 (6)
(6)
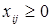 (7)
(7)
Здесь 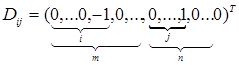 - вектор условия,
- вектор условия,
G=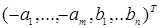 - вектор ресурсов.
- вектор ресурсов.
Известно, что каждой ЗЛП соответствует двойственная задача. В двойственной задаче столько же переменных, сколько ограничений в исходной, и столько же ограничений, сколько в исходной задаче переменных.
Пусть 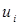 - двойственная переменная, соответствующая i-тым ограничениям (2) (потенциал пункта Аi),
- двойственная переменная, соответствующая i-тым ограничениям (2) (потенциал пункта Аi), 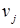 - двойственная переменная, соответствующая j-тому ограничению (3) (потенциал пункта Вj). Тогда вектор двойственных переменных будет иметь вид:
- двойственная переменная, соответствующая j-тому ограничению (3) (потенциал пункта Вj). Тогда вектор двойственных переменных будет иметь вид: 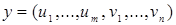 , а сама двойственная задача запишется в виде:
, а сама двойственная задача запишется в виде:
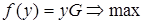 (8)
(8)
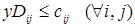 (9)
(9)
В скалярной форме эта задача запишется:
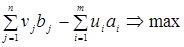 (10)
(10)
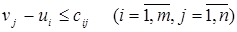 (11)
(11)
Существует теорема (без доказательства):
Для оптимальности опорного плана 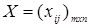 КТЗ (1)-(4) необходимо и достаточно существование вектора двойственных переменных, компоненты которого удовлетворяют условию:
КТЗ (1)-(4) необходимо и достаточно существование вектора двойственных переменных, компоненты которого удовлетворяют условию:
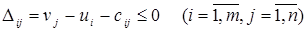 (12)
(12)
Причем 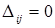 , если
, если 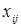 - базисная переменная, и
- базисная переменная, и 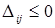 , если
, если 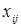 - небазисная переменная.
- небазисная переменная.
Т.о. из теоремы следует, что если хотя бы для одной небазисной переменной 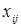
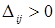 , то опорный план неоптимален и его требуется улучшить.
, то опорный план неоптимален и его требуется улучшить.
Т.о., для проверки опорного плана 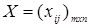 на оптимальность необходимо определить потенциалы
на оптимальность необходимо определить потенциалы 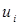 ,
, 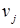 всех пунктов Аi и Вj. Для этого используют условие (12) для базисных переменных:
всех пунктов Аi и Вj. Для этого используют условие (12) для базисных переменных:
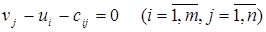 (13)
(13)
Для отыскания потенциалов 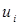 ,
, 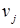 необходимо решить данную систему линейных уравнений. Уравнений в системе (13) будет (m+n-1), а кол-во неизвестных (m+n). Поэтому любой одной переменной можно придать любое значение, в том числе и нулевое. На распределительной таблице построение потенциалов производится следующим образом: полагаем для какой-либо строки i1, содержащей базисные переменные, потенциал
необходимо решить данную систему линейных уравнений. Уравнений в системе (13) будет (m+n-1), а кол-во неизвестных (m+n). Поэтому любой одной переменной можно придать любое значение, в том числе и нулевое. На распределительной таблице построение потенциалов производится следующим образом: полагаем для какой-либо строки i1, содержащей базисные переменные, потенциал 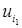 =0. Просматривается эта строка, и находятся базисные клетки
=0. Просматривается эта строка, и находятся базисные клетки 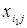 . Для всех таких клеток из (13) можно определить потенциалы столбцов Вj:
. Для всех таких клеток из (13) можно определить потенциалы столбцов Вj: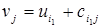 . Далее по известным потенциалам столбцов можно определить потенциалы некоторых строк. Пусть потенциал
. Далее по известным потенциалам столбцов можно определить потенциалы некоторых строк. Пусть потенциал 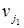 известен. Тогда просматривается столбец с номером
известен. Тогда просматривается столбец с номером 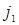 и находятся клетки (
и находятся клетки (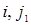 ), содержащие базисные переменные. Для всех этих клеток из (13) можно найти потенциалы строк Аi:
), содержащие базисные переменные. Для всех этих клеток из (13) можно найти потенциалы строк Аi: 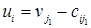 . Продолжая этот процесс, найдутся потенциалы строк
. Продолжая этот процесс, найдутся потенциалы строк 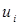 всех пунктов производства и потенциалы столбцов
всех пунктов производства и потенциалы столбцов 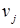 всех пунктов потребления.
всех пунктов потребления.
Далее для всех клеток (i,j) содержащих небазисные переменные, вычисляются оценки 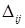 . Если все
. Если все 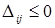 , то рассматриваемый план КТЗ является оптимальным. Если хотя бы для одной клетки (k,l) справедливо
, то рассматриваемый план КТЗ является оптимальным. Если хотя бы для одной клетки (k,l) справедливо 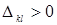 , то опорный план неоптимален и необходимо перейти к лучшему опорному плану.
, то опорный план неоптимален и необходимо перейти к лучшему опорному плану.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 230; Нарушение авторских прав?; Мы поможем в написании вашей работы!