Агрегатные состояния вещества. Уравнение Ван дер Ваальса. Фазовые переходы

По мере увеличения плотности газа становится существенным взаимодействие между молекулами. Увеличение давления может сопровождаться превращением газа в жидкость, среду со свойствами существенно отличными от свойств газа, тем более идеального газа.

Эти явления связаны с взаимодействием молекул между собой. Выяснить в деталях характер этого взаимодействия в данном разделе физики не представляется возможным, однако, можно привести факты, а в дальнейшем их использовать, показывающие, что на близких расстояниях молекулы отталкиваются (газ нельзя сжать до бесконечно малого объема, а на больших – притягиваются (жидкость не распадается на молекулы, самопроизвольно не превращается в пар).

Учтем эти силы в уравнение состояния идеального газа:

- силы отталкивания не позволяют сжать газ до бесконечно малого объема, поэтому, вместо 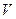в уравнении 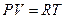, запишем 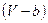. При этом получим 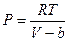. Видно, что при ,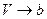

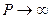- силы притяжения уменьшают давление, т.к. они стремятся сжать газ. Поправку к давлению учтем следующим образом. На каждую молекулу действует сила пропорциональная плотности газа 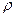~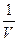, где 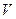-объем, но давление тем меньше, чем больше молекул, т.е. опять имеем пропорциональность 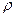. Таким образом поправка к давлению ~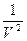. Обозначим эту поправку как 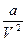, где 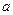- некоторая константа, характеризующая силы притяжения молекул. Поэтому имеем:

-

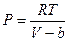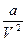
или, для одного моля вещества, получаем:

.

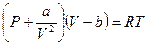Это уравнение состояния реального газа или, как его еще называют, уравнение Ван дер Ваальса. Коэффициенты 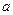и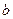называются константами Ван дер Ваальса. Они зависят от типа газа.

При малых плотностях газа, когда 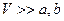, поправками Ван дер Ваальса можно пренебречь и получить уравнение состояния идеального газа.

Представим полученное уравнение в виде:

.

Это уравнение третей степени, следовательно, оно имеет три корня. Анализ показывает, что отрицательных корней нет, а корни либо все три действительные, либо один действительный и два комплексно сопряженных.

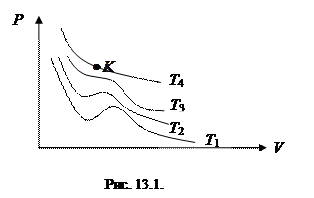
На 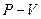-диаграмме (рис. 13.1) представлены изотермы Ван дер Ваальса для различных температур: .

Видим, что при низких температурах изотермы реального газа существенно отличаются от изотермы идеального газа.

Рассмотрим на изотерме реального газа (рис. 13.2) следующие участки:

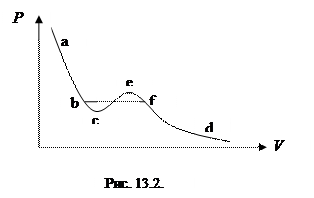(a-c) и (e-d) - на этих участках с ростом объема уменьшается давление, что находится в соответствии с экспериментом.

(с-e) – этот участок изотермы на практике не реализуется.

Как показывает опыт реальной изотерме Ван дер Ваальса соответствует кривая (a-b-f-d).

Участок (a-b) соответствует газообразному состоянию, (f-d) – жидкому, горизонтальный участок (b-f) - переходному двухфазовому состоянию вещества, в котором две фазы жидкая и газообразная находятся одновременно. Причем для данного вещества этому переходу соответствует определенное давление, определяемое температурой.

Участки (e-f) и (b-c) отвечают метастабильным состояниям: переохлажденному пару (газу) и перегретой жидкости соответственно.

При повышении температуры прямолинейный участок (b-f) сужается до точки (К). Это критическая точка (см. рис.13.1). В этой точке при фазовом переходе объем сохраняется, а производная . Температура, при которой это происходит называется критической (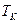). При - преобразования фазовых состояний нет, существует только газообразная фаза. При 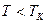возможно существование как жидкой, так и газообразной фаз.

Из изотерм Ван дер Ваальса видно, как сделать газ жидкостью. Для этого необходимо охладить газ до температуры ниже критической и потом сжать.

Дата добавления: 2014-01-05