Коэффициент теплопроводности

Для нахождения коэффициента теплопроводности не требуется проведения каких либо дополнительных вычислений, т.к. процессы диффузии и теплопроводности является аналогичными. При этом роль коэффициента диффузии в процессе переноса тепла играет коэффициент температурапроводности (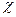), т.е. имеем

~.

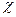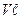15.6. Теплосопротивление

Выражение плотности потока тепла позволяет решать различные задачи по теплопроводности. Рассмотрим одну из них.

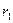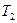Пусть имеется слой вещества, ограниченный двумя концентрическими сферами, с радиусами и , поддерживаемыми при температурах и соответственно. Требуется найти стационарное значение полного потока тепла от сферы 1 к сфере 2. Для нашего случая имеем:

.

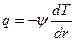Согласно закону сохранения энергии можно констатировать, что полный поток тепла через сферу любого радиуса одинаков. Т.е.

,

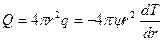откуда следует, что:

.

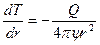Интегрируя последнее выражение получим:

.

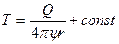Знаем, что при 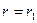температура 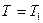. Поэтому имеем:

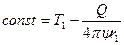
и как следствие этого получаем:

.

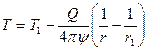Теперь подставим в это выражения параметры второй сферы и получим:

,

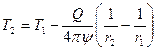и определим искомую величину:

.

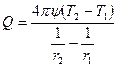Из полученного выражения видно, что если удалить вторую сферу на бесконечность (), то

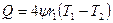
и полный тепловой поток не зависит от 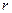, а определяется только разностью температур тела и бесконечности.

Отношение разности температур к тепловому потоку называется теплосопротивлением. В частности, для сферического слоя теплосопротивление 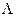равно:

.

15.7. Внутреннее трение в газах. Вязкость

Представим себе плоскость, разделяющую два слоя движущегося газа так, что слой №1 движется со скоростью 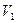, слой №2 – со скоростью . Пусть 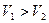. Молекулы в слое №1, в на-

правлении потока газа, обладают большим количеством движения, чем молекулы слоя №2. За счет теплового движения, молекулы из слоя №1 попадают в слой №2, а из слоя №2 в слой №1, перенося с

собой количество движения в направлении потока газа. Происходит обмен количеством движения. Первый слой замедляется, второй – ускоряется. Изменение количества движения в единицу времени определяет силу, силу трения между слоями газа. Это сила внутреннего трения или сила вязкости. Ее причина в обмене количеством движения в направлении потока между слоями газа (жидкости) за счет теплового движения частиц.

Получим выражение для коэффициента вязкости.

Для этого изобразим плоскость 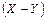и отстоящие от нее на расстояниях, равном средней длине свободного пробега частиц 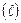, две другие плоскост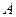и и 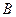, где газ движется со скоростям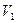и и . Таким образом градиент скорости будет равен . Выделим единичную поверхность на плоскости 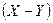и найдем количество движения, переносимое через нее в единицу времени. Испытав последнее столкновение (в среднем) на расстоянии 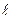от плоскости 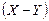молекулы с вероятностью 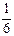движутся в направлении соседнего слоя (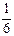-т.к. есть шесть возможных направлений движения и все они равновероятны), перенося при этом в единицу времени массу равную 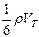, где 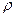- плотность газа, 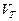- тепловая скорость движения молекул. При этом, из слоя №1 в слой №2 будет перенесено в единицу времени 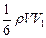количества движения, а из слоя №2 в слой №1 . Разность этих величин определяет избыток количества движение переносимый через единичную площадку в единицу времени, т.е. силу трения:

.

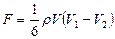Ранее, для силы вязкого трения, было приведено выражение: 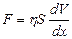, которое для нашего случая (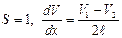) принимает вид:

.

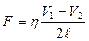Сравнивая представленные выражения для силы трения, получаем:

.

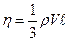Известно, что произведение 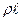для данного типа газа величина постоянная, поэтому сила вязкого трения для газов не зависит от плотности газа – это закон Максвелла. Закон был проверен Бойлем в экспериментах по изучению затухания маятника в газе при различных его давлениях и был подтвержден. Объяснение заключается в том, что изменение плотности газа приводит к изменению средней длины свободного пробега его молекул.

Заключение.

Рассмотренные явления: диффузия, теплопроводность, вязкость, называются явлениями переноса, переноса вещества, энергии, количества движения, которые осуществляются за счет теплового движения частиц. Было получено, что ~ .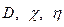

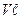15.8. Свойства газов при низких давлениях

Если средняя длина свободного пробега молекул газа превышает характерные размеры объема, в котором он находится, то его свойства будут существенно отличаться от свойств идеального газа. Это различие обусловлено тем, что свойства идеального газа определяются столкновениями между молекулами, которые хоть и редко, но происходят.

При давлении в 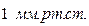и температуре 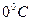средняя длина свободного пробега молекул азота (воздух) составляет примерно , а при давлении она значительно меньше - 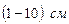и становится сравнимой с размерами лабораторных камер. Такие и большие разрежения газа называются вакуумом. Следует отметить, что и при относительно высоких давлениях всегда можно указать такие размеры сосудов, при которых вакуумные условия будут выполняться. Ясно, что в вакуумных условиях явления переноса уже теряют тот смысл, который они имели ранее. Это сказывается на многих явлениях, происходящих в разреженных газах.

Различие в физических свойствах разреженного и идеального газов покажем на следующем примере. Пусть у нас имеются два объема, содержащие газ, соединенных трубкой. Эти объемы поддерживаются при различных температурах. Найдем отношения установившихся плотностей газов в этих объемах для условий, соответствующих:

а) идеальному газу. В этом случае состояние равновесия достигается при равенстве давлений в сосудах, поэтому, в соответствии с законом Гей-Люссака, имеем:

,

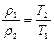б) разреженному газу. В этом случае состоянию равновесия уже соответствует условие равенства потоков молекул перетекающих из одного сосуда в другой, т.е. 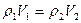или

.

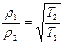СОДЕРЖАНИЕ

Раздел I. Механика поступательного и вращательного

движения тел..................... 3

1. Кинематика......................... 3

1.1. Основные понятия кинематики........... 3

1.2. Законы сложения скоростей и ускорений.....10

2. Основы динамики.................... 12

2.1. Инерциальные системы отсчета.

Первый закон Ньютона...............12

2.2. Масса. Количество движения.

Сила. Второй и третий законы Ньютона......13

2.3. Вращательное движение твердого тела.......17

2.4. Момент инерции...................18

2.5. Кинетическая энергия движения твердого тела..23

2.6. Теорема Штейнера..................23

2.7. Момент количества движения............25

2.8. Момент силы.....................25

2.9. Второй закон Ньютона для вращательного

движения.......................25

2.10. Гироскоп. Скорость прецессии гироскопа.....26

2.11. Закон сохранения массы и количества движения.

Реактивное движение.................29

2.12. Закон сохранения момента количества движения.32

2.13. Механическая работа. Потенциальная энергия.

Типы равновесий...................33

2.14. Закон сохранения энергии.............. 36

2.15. Применение законов сохранения.

Упругое соударение шаров............. 38

2.16. Силы упругости. Закон Гука............. 40

2.17. Силы трения...................... 45

2.18. Силы тяготения. Потенциальная энергия

гравитационного поля. Вес. Ускорение свободного

падения........................ 46

2.19. Силы инерции..................... 51

3. Механические колебания и волны............ 52

3.1. Гармонические колебания.............. 52

3.2. Потенциальная, кинетическая и полная энергия

тела, совершающего гармонические колебания.. 57

3.3. Пружинный, математический и физический

Маятники........................ 58

3.4. Затухающие колебания............... 65

3.5. Вынужденные колебания............... 68

3.6. Параметрический резонанс.............. 73

3.7. Сложение колебаний одинакового направления.. 77

3.8. Сложение колебаний взаимно перпендикулярного

направления...................... 78

3.9. Негармонические периодические колебания.

Гармонический анализ................ 81

3.10 Механические волны. Фазовая скорость волны... 82

3.11 Фазовая и групповая скорость распространения

Волн. Дисперсия. Формула Рэлея.......... 85

3.12. Стоячая волна..................... 88

3.13. Эффект Допплера................... 89

3.14. Акустические волны. Звук.............. 91

4. Основы гидродинамики и аэродинамики........ 93

4.1. Уравнение неразрывности струи........... 94

4.2. Уравнение Бернулли................. 95

4.3. Течение вязкой жидкости.............. 97

4.4. Сопротивление движению тел в жидкостях и

газах......................... 101

4.5. Кинематическая вязкость. Число Рейнольдса... 104

4.6. Аэродинамические силы............... 106

Раздел II. Молекулярная физика и термодинамика..... 109

1. Основные макропараметры систем......... 109

1.1. Температура..................... 109

1.2. Давление....................... 111

2. Идеальный газ.

Уравнение состояния идеального газа........ 112

3. Закон Бойля Мариотта, Гей Люссака, Шарля,

Дальтона........................ 115

3.1. Закон Бойля Мариотта................ 115

3.2. Закон Гей Люссака.................. 115

3.3. Закон Шарля..................... 116

3.4. Закон Дальтона................... 116

4. Идеальный газ во внешнем силовом поле.

Распределение Больцмана.

Барометрическая формула............... 117

5. Распределение частиц по скоростям при

тепловом равновесии. Распределение Максвелла.. 119

6. Работа при тепловых процессах............ 120

6.1. Работа при изобарном процессе........... 122

6.2. Работа при изохорном процессе.......... 122

6.3. Работа при изотермическом процессе....... 122

7. Закон сохранения энергии при тепловых

процессах. Первое начало термодинамики...... 123

8. Теплоемкость..................... 124

8.1. Теплоемкость при постоянном объеме и

постоянном давлении................ 124

8.2. Теплоемкость одноатомного газа......... 125

8.3. Теплоемкость двухатомного газа.......... 126

8.4. Теплоемкость твердого тела.

Закон Дюлонга и Пти................ 127

9. Адиабатический процесс............... 127

10. Цикл Карно...................... 130

11. Необратимость тепловых процессов......... 132

12. Второе начало термодинамики............ 133

13. Агрегатные состояния вещества.

Фазовые переходы. Уравнение Ван дер Ваальса... 134

14. Жидкости........................ 137

14.1. Поверхностные явления............... 137

14.2. Капиллярные явления................ 141

14.3. Упругость пара над искривленной поверхностью.142

14.4. Тройная точка.................... 143

14.5. Кристаллические модификации.......... 145

14.6. Фазовые переходы первого и второго рода.... 146

15. Столкновения молекул и явления переноса..... 147

15.1. Диффузия. Теплопроводность.

Температурапроводность.............. 148

15.2. Средняя длина свободного пробега молекул.

Среднее время свободного пробега молекул.

Средняя частота столкновений молекул...... 149

15.3. Прицельный параметр и эффективная

частота столкновений молекул........... 150

15.4. Коэффициент диффузии.............. 151

15.5. Коэффициент теплопроводности.......... 152

15.6. Теплосопротивление................. 152

15.7. Внутреннее трение в газах. Вязкость........ 154

15.8. Свойства газов при низких давлениях....... 157

Дата добавления: 2014-01-05