Строительная продукция

Пример 2.

Примеры решения типовых задач

Задачи для самостоятельной работы

Первообразная и неопределенный интеграл.

Первообразная и неопределенный интеграл.

Лекция № 7

Волгодонск

Определение: Первообразной F(x) для функции f(x) на промежутке называют функцию, производная которой.

Пример. Для функции: первообразная на R, так к при любом х.

Лемма.Если производная функции на промежутке, то.

Доказательство: По теореме Лагранжа для любых x₁, x₂ Î выполняется, где, так как Þ Þ Þв силу произвольности точек x₁ и x₂ F(x) = C(const).

Ч.т.д.

Теорема: Пусть функция F(x) – первообразная f(x), Ф(x) – другая первообразная f(x) Þ F(x)=Ф(x)+С.

Доказательство: так как Þ по Лемме Þ.

Ч.т.д.

Таким образом, из теоремы следует, что выражение описывает все множество первообразных функции f(x).

Определение: Неопределенным интегралом функции f(x) по переменной x называется множество всех её первообразных, где.

ò ‒ знак интеграла, f(x) – подынтегральная функция, x – переменная интеграла, ‒ подынтегральное выражение, С – const интегрированная.

Вычисление неопределенного интеграла называют интегрированием. Проверить правильность вычисления неопределенного интеграла можно продифференцировав результат.

; - верно

Свойства неопределенного интеграла.

Замена переменных в неопределенном интеграле.

Пусть функция является дифференцируемой и обратимой, на множестве значений которой определена функция Þ =.

Пример: = = = = = =.

Пример: = = =e^t+C=e^{sin x}+C.

Таблица интегралов.

	, n≠-1

Теоретические вопросы для самопроверки.

1. Что такое первообразная?

2. Что такое неопределённый интеграл и в чём отличие его от первообразной?

3. Какие свойства неопределённого интеграла знаете?

4. Зачем нужна замена переменных в неопределенном интеграле?

а); б); в)

1.Замена переменных

Пример 1. Найти.

Решение:

Решение:

Пример 3. Найти.

Решение:

Виды строительных процессов:

1. Объектный

2. Специализированный

3. Частный

Виды строительной продукции:

1. Здания и другие сооружения

2. Часть здания, конструктивный элемент здания

3. Элемент строительной конструкции

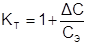Технологичность строительной продукции

Коэффициент технологичности: Где

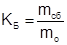Коэффициент равновесности:

Коэффициент блочности:

Коэффициент технологичности стыков:

Основные элементы строительного процесса:

1. Трудовые ресурсы

2. Материальные ресурсы

3. Технические средства

Дата добавления: 2014-01-05