Основні положення символічного методу

Раніше ми розглянули розрахунок електричних кіл синусоїдного струму методом векторних діаграм та методом еквівалентних опорів і провідностей. Ці методи є достатньо складними, особливо при розрахунку розгалужених та складних електричних кіл.

Тому широке практичне застосування одержав символічний метод розрахунку кіл синусоїдного струму. (Метод був введений американським вченим Штейнметчем, в Росії його став застосовувати академік Міткевич).

Для наочності розрахунок електричних кіл символічним методом супроводжується побудовою векторних діаграм.

Символічний метод оснований на застосуванні комплексних чисел.

З математики відомо, що комплексне число можна виразити точкою, або радіус-вектором на комплексній площині (рис. 3.24) і записати аналітично в трьох формах: алгебраїчній, тригонометричній та показниковій:

,

де A= – модуль комплексного числа;

– аргумент комплексного числа;

cos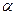+ j sin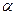=e – Формула Ейлера.

01 – вісь дійсних чисел;

0j – вісь уявних чисел.

Для переходу від однієї форми комплексного числа до іншої використовуються такі формули:

,

,

.

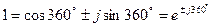При додаванні або відніманні краще використовувати алгебраїчну форму запису, а при множенні та діленні – показникову форму.

Наприклад: _.

; .

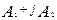
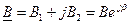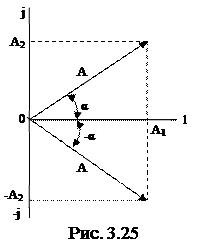
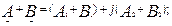
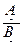
Два комплексних числа називаються спряженими, якщо їх модулі рівні, а аргументи рівні, але протилежні за знаком (рис. 3.25)

;

.

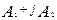
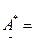
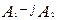
Добуток комплексно-спряжених чисел дорівнює дійсному числу:

.

Таким чином, комплексне число можна подати радіус-вектором і навпаки, – радіус-вектор може бути поданий комплексним числом.

Зобразимо вектор струму І_m на комплексній площині під кутом α= ψ_і (рис. 3.26):

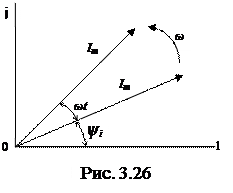Як радіус-вектор його можна записати в комплексній формі:

.

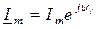Примусимо вектор І_m обертатися з частотою ω. Тоді через час t він займе положення α=ωt+ψ_і. Вектор, що обертається, в комплексній формі записується у вигляді:

= І_m e^j(ωt+ψі)=I_m e^jψі e^jωt=e^jωt,

де – комплексний миттєвий струм,

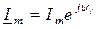. – комплексна амплітуда струму,

– оператор обертання.

Запишемо комплексний миттєвий струм в тригонометричній формі:

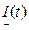= I_m cos(ωt+ψ_і)+jI_m sin(ωt+ψ_і).

Бачимо, що синусоїдну функцію можна подати у вигляді уявної частини комплексного числа, тобто проекції радіус-вектора на вісь уявних чисел. Умовно це записується так:

i=I_m sin(ωt+ψ_і)=J_m(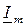e^jωt).

Символ J_m (уявний) означає, що при переході від комплексного числа до синусоїдної функції, необхідно брати лише уявну частину. Можна записати іншим чином:

i=I_m sin(ωt+ψ_і) e^jωt= ,

де i – оригінал; –знак відповідності;

– зображення – це допоміжна величина, що не має фізичного змісту, але зручна для розрахунку.

Отже, комплексним числом можна зобразити синусоїдну функцію.

Аналогічно

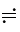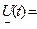
u e^jωt; =e^jψu; 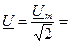U e^jψu;

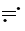e= e^jωt; e^jψе; e^jψе.

Приклад:

1. Дано: i =10sin(ωt+30) A. Визначимо ,.

= I_m e^jψі=10 e^j30 A. = A.

2. Дано: 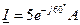. Визначимо , i.

i=I_m sin(ωt+ψ_і)=5sin(ωt-60) A,

= I_m e^jψі=5e^–j60 A.

Дата добавления: 2014-01-05