Приклади розрахунку перехідних процесів

Задача № 1

На кінці лінії постійного струму в навантаженні відбулося коротке замкнення. Електромагнітне реле захисту від короткого замикання з внутрішніми параметрами R, L, вимкнуло своїми контактами S_p (рис. Р13.1) лінію від джерела енергії, коли струм в ній досяг значення 30 А. Визначити закон зміни струму в лінії і проміжок часу, за який спрацює реле після короткого замикання, якщо R=3 Ом, L=0,2 Гн, R_л=2 Ом, R_н=20 Ом, U=200 B.

Рішення

1. Визначимо контур, в якому протікає перехідний процес.

Після виникнення короткого замикання (ввімкнення вимикача S на
рис. Р8.1) перехідний процес буде протікати в контурі, що включає реле з параметрами R, L та контактом S_р, опір лінії R_л та джерело енергії з
напругою U.

2. Позначимо напрям перехідного струму та обходу контуру.

3. Визначимо незалежні початкові умови із контуру до комутації з врахуванням вибраного напряму перехідного струму:

i_L(0)=I=.

Такий струм протікав в колі до короткого замикання.

4. Складаємо рівняння перехідного процесу для контуру після комутації:

.

5. Рішення диференціального рівняння шукаємо в вигляді суми двох складових: і=і_ус+і_в.

Для визначення усталеної складової перехідного струму і_ус розрахуємо коло після закінчення перехідного процесу:

i_ус=.

Вільну складову перехідного струму і_в шукаємо як загальне рішення однорідного рівняння:

в вигляді: ,

де р – корінь характеристичного рівняння:

(R+R_л )+ pL=0,

звідки .

Тому ,

де – стала часу кола.

Таким чином і=і_ус+і_в=40+Ае^-25t A.

6. Сталу інтегрування А знаходимо із початкових умов при t=0:

і(0)=і_ус(0)+і_в(0), 8=40+А, А= - 32 А.

Тепер можемо записати кінцевий вираз для перехідного струму:

і=40 - 32е^-25t A. (1)

7. Визначимо проміжок часу t_c, за який спрацює реле після виникнення короткого замикання.

За умовою реле спрацює, коли перехідний струм досягне значення 30А. Підставимо це значення струму в рівняння (1) і розрахуємо його відносно часу t=t_c:

30=40-32, або 32=10.

Тоді , .

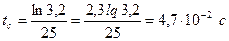8. Побудуємо часову діаграму і(t), для цього спершу окремо побудуємо усталену складову перехідного струму
і_ус = 40 А – це пряма,
та вільну складову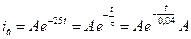

в масштабі часу, кратному сталій часу кола τ=0,04 с.

Пам’ятаємо, що за інтервал часу τ вільна складова зменшується в е (е=2,71…) раз. Перехідний струм і знаходимо як суму і=і_ус+і_в. За кривою і(t) для струму І=30 А визначаємо час спрацювання реле t_{c .} (рис. Р13.2).

Задача № 2

Коло зі змішаним з’єднанням елементів R₁, C, R₂ знаходиться під постійною напругою U=120 В. Визначити закони зміни перехідних напруг на конденсаторі і струму в ньому після вимикання вимикача, якщо R₁=40 Ом, R₂=20 Ом, С=50 мкФ
(рис. Р13.3).

Рішення

1. Показуємо в контурі, де протікає перехідний процес, напрямок перехідного струму і та напруги на конденсаторі u_c і обхід контуру за напрямом перехідного струму.

2. Визначимо незалежні початкові умови u_c(0) з кола до комутації:

.

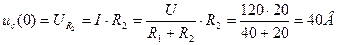3. Складемо рівняння перехідного процесу для контуру після комутації, в якому протікає перехідний струм:

, або , де .

4. Рішення цього рівняння шукаємо в вигляді суми двох складових:

Усталену складову u_cус знаходимо в колі після комутації для усталеного режиму:

.

В усталеному режимі струм в колі не протікає, тому u_R1= 0, а

u_сус=U=120 В.

Вільну складову u_св знаходимо як загальне рішення однорідного рівняння

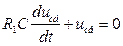
в вигляді: u_cв=Ае^Pt,

де р - корінь характеристичного рівняння R₁C p+1= 0.

.

Таким чином .

5. Визначимо сталу інтегрування А із початкових умов:

,

звідки А =- 80 В.

Кінцевий вираз для перехідної напруги на конденсаторі має такий вигляд:

.

6. Знаходимо перехідний струм:

Задача № 3

Електричне коло (рис. Р13.4) підключене до джерела постійного струму. Визначити закони зміни струмів в гілках і₁, і₂ і напруги на вході кола u_аб після вимкнення вимикача, якщо R₁=R₂=10 Ом,
J=2 A, С=100 мкФ.

Рішення

1. Показуємо напрямок перехідних струмів в гілках.

2. Визначаємо незалежні початкові умови u_c(0) з кола до комутації:

так як джерело струму замкнене накоротко, то u_c(0)= u_аб(0)= 0.

3. Складемо рівняння за I-м законом Кірхгофа для вузла «а»:

і₁+і₂=J.

Наступні перетворення будемо здійснювати відносно струму і₂ враховуючи, що: ,

отримаємо:

або, враховуючи, що

4. Вирішимо отримане рівняння, рішення будемо шукати в вигляді:

де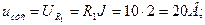

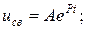
р – корінь характеристичного рівняння, рівний:

.

Таким чином

.

5. Визначимо сталу інтегрування А із початкових умов при t=0:

Тоді .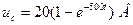

6. Визначимо перехідні струми в гілках:

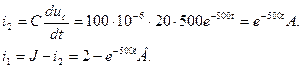
7. Визначимо напругу на вході кола

.

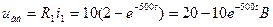Задача № 4

Знайти перехідну напругу на обкладинках конденсатора після вимикання вимикача S в колі рис. Р13.5, якщо u=200sin(1000t+ψ_u) B,
R=50 Ом, L=0,05 Гн, С=20 мкФ і при t=0 напруга, зростаючи, досягає позитивної величини, рівної її діючому значенню.

Рішення

1. Попередньо знаходимо початкову фазу прикладеної напруги u із умови:

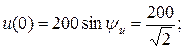
або 135°.

В нашому випадку ψ_u =45°, так як комутація виконується в той момент, коли напруга зростає в області позитивних значень.

Таким чином:

.

1. Знаходимо напругу на конденсаторі в колі до комутації:

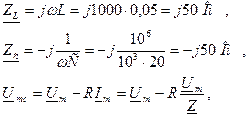
де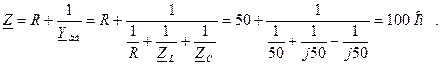

В показовій формі:

.

Переходячи до тригонометричної форми, отримаємо напругу на конденсаторі до комутації:

2. Визначаємо незалежні початкові умови:

3. Складемо рівняння перехідного процесу за ІІ-м законом Кірхгофа для контуру R,C відносно u_c:

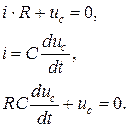
4. Вирішимо складено рівняння:

5. При t=0:

u_c(0)=u_cус(0)+u_cв(0),

.

Тому .

Задача № 5

Визначити перехідний струм при включенні кола рис. Р13.6 на постійну напругу , якщо ; ; .

Рішення

1. Відповідно до полярності прикладеної напруги вказуємо на схемі (рис. Р8.6) позитивний напрямок перехідного струму.

2. На підставі закону Ома складемо вираз для перехідного струму в операторній формі:

.

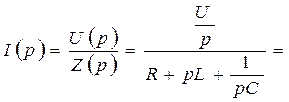
3. За допомогою теореми розкладання за знайденим операторним струмом знайдемо перехідний струм

.

Знайдемо корні рівняння ,

, ,

Обчислимо значення похідної при знайдених коренях

,

,

.

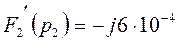Знайдемо значення :

.

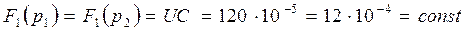Підставимо у формулу розкладання числові значення величин:

.

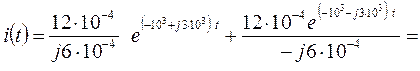
При необхідності будь-яку перехідну напругу на ділянці кола можна знайти відразу, не обчислюючи струм. Наприклад:

Застосувавши до цього виразу теорему розкладання, знайдемо .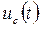

Задача № 6

Розрахувати перехідний процес при відключенні кола рис. Р13.7 від джерела постійної напруги, якщо

Рішення

При вимиканні рубильника S утвориться коло з послідовним з’єднанням R, та , до якого можна застосувати закон Ома для ненульових початкових умов.

1. Задамося напрямками перехідних струму, напруги на конденсаторі та обходу контуру (рис. Р13.7).

2. Визначимо значення струму в котушці та напруги на конденсаторі в колі до комутації з врахуванням вибраного напряму перехідного процесу:

, "+" – тому, що співпадає з ;

u_c(0)= - U= - 150 B.

3. Складемо вираз для операторного перехідного струму за законом Ома для ненульових початкових умов:

.

так як немає джерела енергії в контурі після комутації.

4. За допомогою теореми розкладання за операторним струмом знайдемо перехідний струм:

.

Визначимо корені рівняння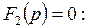

, , , ,

.

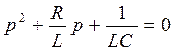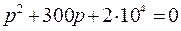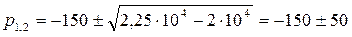Визначимо похідну 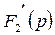та її значення при знайдених коренях:

.

,

.

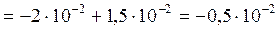Знайдемо значення :

,

Підставивши у формулу розкладення числові значення величин, отримаємо:

5. Зробимо перевірку

1) На відповідність початковим умовам:

при t =0 .

2) На відповідність усталеним значенням:

при .

Умови задачі задовольняються.

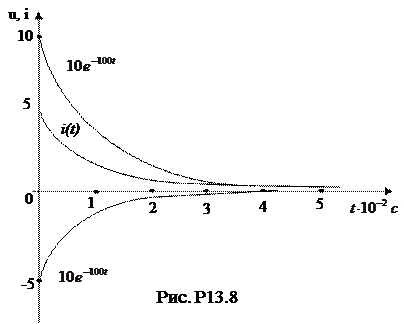
4. Побудуємо криву перехідного струму (рис. Р13.8). При побудові складових перехідного струму враховуємо, що 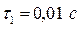а .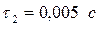

Задача № 7

Розрахувати класичним методом перехідний струм в резисторі R ₃
(рис. 13.9) а також інші перехідні струми та напругу на конденсаторі, якщо: U =10 B, R ₁ =50 Ом, R ₂ =16,67 Ом, R ₃ =33,33 Ом, С=1 мкФ.

Розв’язок.

1. Аналізуємо схему. Бачимо, що в усталеному режимі до комутації струм через R ₃ не протікав, а після комутації в усталеному режимі він дорівнює струму І₂. Для розрахунку перехідного процесу задаємо напрями перехідних струмів і₁, і₂, і₃, напруги на конденсаторі u_с та обходу контурів.

За класичним методом перехідний струм і₃ в резисторі R ₃ (як і інші перехідні струми та напруги) знаходимо як суму вільної та усталеної складових:

і₃= і_3у+ і_3в.

2. Визначаємо початкові умови.

Спершу із кола до комутації (рис. 13.9,а) визначаємо незалежні початкові умови, в даному колі це напруга на конденсаторі u_с(0). Конденсатор представлений розривом вітки, тому що постійний струм по ньому не протікає.

u_с(0)= І₂ R₂, де І₂=І₁=U/(R₁+ R₂)=0,15 А, тому u_с(0)=2,5 В.

Тепер визначаємо залежні початкові умови із схеми після комутації (рис. 13.9,б) з урахуванням незалежних початкових умов:

із контуру І маємо:

і₃(0₊)= і₂(0₊)= u_с(0)/(R₃+ R₂)=0,05 А,

із зовнішнього контуру:

і₁(0₊)=(U - u_с(0))/ R₁=0,15 А,

за І законом Кірхгофа:

і_с(0₊)= і₁(0₊) - і₂(0₊)=0,1 А.

3. Для кола після комутації складаємо за законами Кірхгофа систему рівнянь перехідного процесу і вирішуємо її відносно і₃ чи будь-якої іншої невідомої величини. В нашому випадку це краще зробити відносно u_c.

і₁= і₂+ і_c, і_c =С d u_c / dt,

u_c – U + і₁ R₁ =0, → і₁=(U - u_c )/ R₁,

u_c – і₂ (R₂+R₃ ) =0, → і₂=- u_c /(R₂+ R₃ ).

Підставивши значення струмів в перше рівняння, отримаємо:

R₁ (R₂+R₃ ) С d u_c / dt +(R₁ +R₂+R₃ ) u_c = U (R₂+R₃ ).

Рішення цього неоднорідного диференціального рівняння першого порядку за класичним методом шукаємо в вигляді:

u_c = u_{c у}+ u_{c в}= u_{c у}+ = u_{c у}+ .

Аналогічно знаходимо і всі струми, наприклад:

і₃= і_3у+ і_3в= і_3у+ 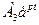= і_3у+ ,

де:

р – корінь характеристичного рівняння;

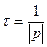– стала часу.

Корінь характеристичного рівняння р знаходимо з характеристичного рівняння, записаного на основі отриманого уже однорідного диференціального рівняння (праву частину прирівнюємо нулю) шляхом заміни

d u_c / dt → р, u_c → 1.

Маємо

­ – характеристичне рівняння.

Характеристичне рівняння можна також скласти за методом комплексного опору. Наприклад, за комплексним вхідним опором кола після комутації (можна відносно розімкнутих затискачів будь-якої гілки)

шляхом заміни на р та прирівнявши Z(p) до нуля маємо:

, ,

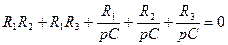­ – характеристичне рівняння,

звідки:

.

Стала часу

.

В колі першого порядку (з одним внутрішнім накопичувачем енергії) вільна складова перехідної напруги u_{c в} чи перехідного струму в резисторі R ₃ (як і будь-якого іншого) буде дорівнювати:

; ,

або через сталу часу:

; .

Тому процес знаходження вільної складової в колі першого порядку можна спростити, знаючи, що в колі з R, L

τ=L/R_екв,

а в колі з R, С

τ= R_екв С,

визначивши сталу часу τ не складаючи характеристичного рівняння. Для цього достатньо знайти еквівалентний активний опір кола R_екв відносно затискачів індуктивної котушки чи конденсатора.

В нашому прикладі R_екв відносно затискачів конденсатора дорівнює:

R_екв= Ом.

Тоді τ= R_екв С =25 10^-6 с.

4. Визначимо усталені складові перехідних струмів та напруг із кола після комутації

і_3у= і_2у= і_1у=І= U/(R₁+ R₂+ R₃ )=0,1 А, і_с.у=0,

u_с.у= І (R₂+ R₃ )=5 В.

5. Визначимо сталі інтегрування із початкових умов. При t=0 для струму і₃ маємо:

і₃(0)= і_3у(0)+ і_3в(0)= і_3у(0)+А₃,

звідки

А₃= і₃(0)-і_3у (0),

Оскільки в колах першого порядку і_в(0)=Ае⁰=А,

тому завжди А= і(0)-і_у(0),

тоді рішення за класичним методом (11.1) можна записати так:

і=і_у+ [і(0)-і_у (0)] . (11.2)

Це є загальна форма рішення диференційного рівняння, що описує перехідний процес в лінійному колі з одним накопичувачем енергії.

В колах постійного струму значення і_у(0)= і_у, а в колах змінного струму і_у(0) треба визначати, тому що залежить від початкової фази синусоїди.

6. Записуємо кінцеві вирази перехідних струмів та напруг:

і₃=і_3у+ [і₃(0)-і_3у(0)] =0,1+(0,05-0,1) =0,1- 0,05 А, і₂ = і_{3 ,}

і₁= і_1у+ [і₁(0)-і_1у(0)] =0,1+(0,15-0,1) =0,1+ 0,05 А,

u_c= u_c.у+ [u_c(0)-u_c.у(0)] =5+(2,5-5) =5-2,5 B,

і_с= і_с.у+ [і_с(0)-і_с.у(0)] =0+(0,1- 0) =0,1 А,

або

і_с=Cdu_c /dt=0,1 А.

7. Побудуємо графік перехідного струму і₃, для чого графічно складемо усталену та вільну складові струму (рис. 13.9,в).

Усталена складова і_3у – це пряма лінія, паралельна вісі часу. Вільну складову і_3в побудуємо за значеннями в моменти часу, кратні сталій часу τ= 25 10^-6 с. Пам’ятаємо, що за час τ вільна складова зменшується в е = 2,71…раз.

8. Перевірка.

Перевірку правильності розрахунку проведемо за допомогою балансу енергії для вільних складових.

Енергія, що витрачається на тепло:

.

Енергія електричного поля конденсатора:

.

Таким чином .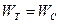

Перевірку можна зробити за відповідністю знайдених перехідних струмів і напруг початковим та кінцевим умовам. Наприклад, перехідна напруга на конденсаторі

при t=0:

u_c(0)=5-2,5е⁰ =2,5 В,

при t= ∞:

u_c(∞)= u_с.у =5-2,5е ^{- ∞} =5 В,

що співпадає з раніше знайденими значеннями.

Задача № 8

Розрахувати перехідний струм в резисторі R ₂ (рис. 13.10), якщо: U =70 B, R ₁ = R ₂ =10 Ом, R ₃ =30 Ом, L = 0,175 Гн.

Розв’язок.

Скористаємося загальною формулою рішення диференційного рівняння, що описує перехідний процес в лінійному колі з одним накопичувачем енергії

і₁=і_1у+ [і₁(0)-і_1у (0)] .

Незалежні початкові умови

і₂(0)= і_L(0)=0.

Дата добавления: 2014-01-05