Компьютерные сети

Проблемы использования множественных регрессионных моделей на практике.

Фиктивные переменные.

Мультиколлинеарность.

Вектор оценок параметров множественной регрессии.

Множественная регрессия.

Парная регрессия.

Парная регрессия – уравнение связи двух переменных у и х: ŷ=f(х), где у – зависимая переменная (результативный признак), х – независимая, объясняющая переменная (признак-фактор). Бывает линейной и нелинейной. Линейная регрессия принимает вид: y=а+bх+e. Нелинейная регрессия бывает 2 видов:

- регрессии, нелинейные по объясняющим переменным, но линейны по оценивающим параметрам:

полиномы разных степеней: y=a+b₁x+b₂x²+…+b_mx^m+e

равносторонняя гипербола: y=a+b/x+e

- регрессии, нелинейные по оценивающим параметрам:

степенная: y=ax^be

показательная: y=ab^xe

экспоненциальная: y=e^a+bxe

Множественная регрессия – изучение взаимосвязи между одной зависимой и двумя или более объясняющими переменными: y_x=f(x₁, x₂, x₃, …, x_m)+ e

Линейные модели множественной регрессии:

y_x=a₀+b₁x₁+b₂x₂+…+b_mx_m+e - для выборки

y_x=a₀+b₁x₁+b₂x₂+…+b_mx_m+e - для генеральной совокупности

Нелинейные модели множественной регрессии:

y_x=a₀*x₁^b1*x₂^b2*…*x_m^bm+e - степенная

y_x=a₀+b₁/x₁+b₂/x₂+…+b_m/x_m+e - гипербола

y_x=a₀+b₁x₁²+b₂x₂²+…+b_mx_m²+e

e_i=y_i-a₀-b₁x₁-…-b_mx_m

Согласно МНК, необходимо найти значения точек а₀, b₁, …, b_m, в которых функция будет минимальное значение: Q=Se_i²=S(y_i-(a₀+Sb_jx_ij))²®min

В множественной регрессии кроме обычных коэффициентов регрессии рассчитывают стандартизированные коэффициенты регрессии (b-коэффициенты). Стандартизированный масштаб необходим в связи с тем, что факторы х могут иметь разные единицы измерения и это может привести к неправильному выводу о силе влияния факторов на y.

t_y=b₁t_x1+b₂t_x2+…+b_mt_xm

t_y=(y-y)/s_y; t_xi=(x_i-x_i)/s_xi; t_y=t_xi=0; s_ty=s_tx=1

Стандартизированные b-коэффициенты показывают, на сколько сигм (квадратичных отклонений) изменяется в среднем результат, если фактор x_i изменится на 1 сигму при неизменном среднем значении других факторов. Для множественной регрессии зависимость следующая: b_i=b_is_y/s_xi

(см. последнюю лекцию в тетради)

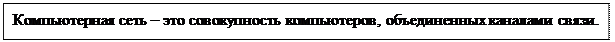
2. Для объединения компьютеров в сеть необходимы:

Ø Сетевое оборудование (сетевая карта в компьютере, соединительные провода).

Ø Сетевые программные средства.

1. Что такое прямое соединение?

Замечание. Простейшее соединение двух компьютеров называется прямым соединением и представляет собой соединение двух компьютеров отрезком кабеля. Для создания прямого соединения компьютеров, работающих под управлением ОС Windows XP, не требуется ни специального аппаратного, ни программного обеспечения. В этом случае аппаратными средствами являются стандартные порты ввода/вывода (последовательный или параллельный), а в качестве программного обеспечения используется стандартное средство, имеющееся в составе ОС (Пуск → Программы → Стандартные → Мастер новых подключений → Установить прямое подключение к другому компьютеру).

12. Каково назначение всех видов компьютерных сетей?

Дата добавления: 2014-01-05