Выбор оптимальных режимов ведения работ в сетевой модели

Литература: 1) Зуковецкий С., Радчик И. Математические методы сетевого планирования, М,: 1965г

2) Моделирование процессов управления. Сборник трудов института гидродинамики. Выпуск 1. Новосибирск: 1967г.

3) Авдеев Ю.А. Выработка и анализ плановых решений в сложных проектах. М., 1971г.

4) Шатров А.И. Разработка сетевых моделей на строительстве сложных объектов. Челябинск, 1989г.

Для выбора оптимальных режимов ведения работ в сетевой модели в исходных материалах по каждой работе задается 2 режима: ненапряженный (когда используется трудовой ресурс с минимальной интенсивностью) и напряженный (когда используется трудовой ресурс с максимальной интенсивностью). В общем виде по каждой работе задается продолжительность и количество рабочих. Обозначим продолжительность через X_ij, а количество рабочих - через Y_ij.

Допущение: X и Y связаны следующей зависимостью:

X_ij • Y_ij = V_ij – трудоемкость

V_ij считается объемом работы и принимается как постоянная величина.

Когда задаются исходные материалы, мы обозначаем продолжительность в ненапряженном режиме через D_ij, а продолжительность в напряженном режиме – d_ij. Соответственно интенсивности будут обозначены: y_ij^(D_ij⁾ и y_ij^(d_ij⁾

y_ij^(D_ij⁾ ≤ y_ij ≤ y_ij^(d_ij⁾

d_ij ≤ x_ij ≤ D_ij

Когда рассматриваем ненапряженный режим, у нас имеется минимальное количество рабочих. Этот минимум рабочих называется ценой сокращения (С_ij). Эту цену принимаем в целом пот модели величиной постоянной.

С_ij = const = y_ij ^(D_ij⁾

Чтобы сократить работу на 14 день, к минимальному количеству рабочих необходимо добавить цену сокращения.

Пример:

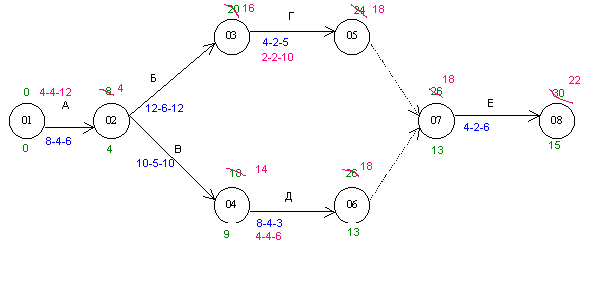
D_ij d_ij C_ij

А – 8 - 4 - 6

6 6 6 6 6 6 6 6

6 х 8 = 48

х

..

..

..

Х

Х

Х

Х

Т^дир = 22

Для того, чтобы приступить к нахождению оптимальных режимов, необходимо определить параметры:

1) определяем Т^р по ненапряженному режиму: Т^р = 30

2) определяем Т^р, соответствующее напряженному режиму: Т^р = 15

3) проверяем имеет ли данная разработка решение на оптимум:

Т^дир ≥ Т^р_{напр. реж.}

Т^дир ≤ Т^р_{ненапр. реж.}

15≤ 22 ≤ 30, следовательно задача имеет решение на оптимум.

4) определяем критический путь по ненапряженному режиму:

КП1 = 01- 02 - 04 - 06 - 07 - 08

5) Т^дир – Т^р_D = 22 – 30 = - 8, следовательно разработку нужно сократить на 8 единиц времени

6) Для того, чтобы выбирать оптимальный режим, нужно, чтобы работала целевая функция

∑∆ y_ij → min

т.е. добавка рабочих должна быть минимальна.

Выбираем работу Д (т.к. цена сокращения минимальна именно на этой работе).

8 - 4 - 3 → 4 - 4 - 6

V = 3 • 8 = 24

7) определяем Т^р измененное: Т^р = 28

8) сравниваем: 22 – 28 = -6

9) определяем критический путь:

КП2 = 01 - 02 - 03 - 05 - 07 - 08

10) выбираем работу Г:

4 - 2 -5 → 2 - 2 - 10

11)определяем Т^р измененное: Т^р = 26

12)сравниваем: 22 – 26 = -4

13)КП3:

03 – 05

01 – 02 07 – 08

04 – 06

14) сокращаем работу А: 8 - 4 - 6 → 4 - 4 - 12

При условии равноценности по показателю С_ij выбор работ может идти по двум направлениям:

1. при увеличении интенсивности достигается максимальное сокращение

2. при равноценности сокращается та работа, которая открывает фронт большему количеству работ

15) определяем Т^р измененное: Т^р = 22

16) сравниваем: 22 - 22 = 0

∆ y = 14 человек; сокращение 8 дней.

При нахождении оптимальных режимов величина y_ij является переменной, которая представляет собой сумму:

y_ij = y_ij^(D_ij⁾ + ∆ y_ij

находим продолжительность:

∆ x_ij = D_ij – x_ij

Постоянно идет сравнение с ненапряженным режимом. В общем виде поиск оптимального режима можно записать следующим образом:

Дана сетевая модель Р

i –j Є P, D,d,c

Т^дир

∆x_ij = D_ij – x_ij

∆ y_ij

Все процедуры по нахождению оптимального режима должны быть направлены на целевую функцию. При этом должны соблюдаться следующие условия:

1. d_ij ≤ x_ij ≤ D_ij

2. T^p_(D) ≥ Т ^дир ≥ Т^р_(d)

3. c_ij и V - const

Первое – технологическое ограничение, второе – организационное ограничение, а третье – требование соответствия целевой функции

∑∆ y_ij → min

после того, как найден оптимальный вариант в целом по проекту, определяются календарные даты и соответствующие планы потребления трудового, материального, машинного и финансовых ресурсов. Оптимальный план исключает значимость критического пути.

Тема № 6: Анализ архитектоники сетевой модели.

6.1. Анализ связей.

6.2. Анализ технологий

6.3. Анализ ресурсных характеристик

Анализ архитектоники (построения, структуры) сетевой модели проводится перед вводом информации о сетевой модели в компьютер. Прежде чем вырабатывать с помощью компьютера решения об оптимальных режимах ведения работ необходимо тщательно проанализировать архитектонику сетевой модели. Во многих литературных источниках этот анализ называется оптимизацией.

Дана сетевая модель:

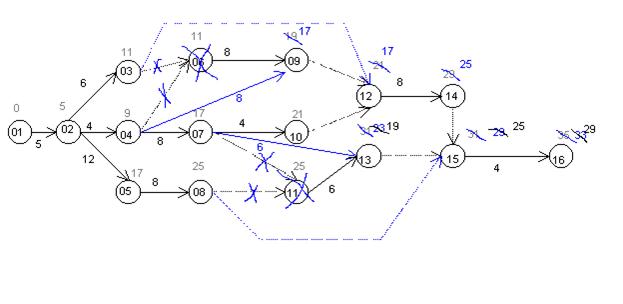
Для рассмотрения принимаем модель первого типа, и допускаем, что характеристикой работ является продолжительность выполнения их в ненапряженном режиме.

Дата добавления: 2014-01-05