Шестая функция сложного процента

Данная функция является функцией расчета денежной суммы, необходимой для погашения стоимости кредита, залога, закладной. Эта сумма выплачивается до полного погашения стоимости при определенном проценте 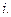Погашение кредита называют истощением или амортизацией актива. А периодически выплачиваемую сумму называют взносом на амортизацию.

Пусть взят кредит в сумме 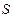на период 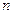промежутков времени под процент 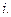Необходимо вычислить размер платежа, вносимого за каждый промежуток времени по погашению этого кредита – т.е. определить взнос на амортизацию. Будем считать, что взнос на амортизацию поступает в конце каждого промежутка времени. Каждый такой взнос к концу срока должен генерировать ту же самую сумму 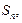что и сумма 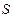, выданная в кредит, под залог и т.д.

Выданная в кредит сумма 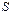согласно первой функции сложного процента через 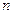промежутков времени составит величину (1.1). Обычный взнос на амортизацию 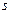за 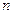промежутков создаст сумму (1.8). Приравнивая выражения (1.1) и (1.8) запишем

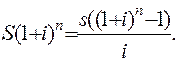(1.20)

Исходя из этого равенства находится взнос на амортизацию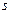

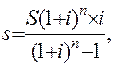(1.21)

или

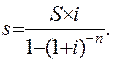(1.22)

Величину

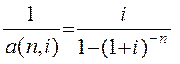(1.23)

называют фактором взноса на амортизацию.

Пример 1.5. На приобретение оборудования для межевания земель государством взят кредит в международном банке стоимостью 50 млн. у.е. на 10 лет под 7% годовых. Какую сумму следует выплачивать в начале каждого года для погашения кредита?

Решение: Следуя (1.21) найдем

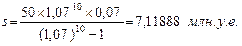
Всего нужно выплатить

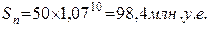
Если же выплату кредита предусматривать в начале каждого года, то из равенства выражений (1.1) и (1.6) можно найти

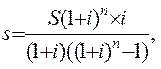(1.24)

или

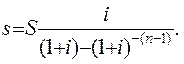(1.25)

Величина (1.25) является авансовым взносом на амортизацию, а функция

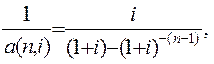
называется фактором этого взноса.

Дата добавления: 2014-01-05