Потери напора

Потери напора подразделяются на две группы: потери напора на трение (или общие) и потери в местных сопротивлениях

.

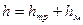а) Потери напора на трение играют решающую роль на участках с плавно изменяющимся течением. Частным случаем такого течения является течение в круглых прямых трубах постоянного сечения, для которых потери напора на трение определяются по формуле

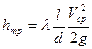, (5.15)

где l - безразмерный коэффициент сопротивления трения; l – длина участка трубы; d – диаметр трубы.

Коэффициент сопротивления в общем случае зависит от числа Рейнольдса и шероховатости трубы.

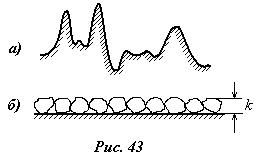
Под технической шероховатостью понимаются неровности стенок трубы, распределение которых носит случайный характер, как это показано в большом масштабе на рис.43,а. Среднюю величину такой шероховатости определить практически невозможно, поэтому для характеристики натурной технической шероховатости вводится понятие эквивалентной зернистой шероховатости, образованной искусственными зернами (чаще всего это калиброванный песок) высотой k (рис.43,б). При этом эквивалентной называется такая зернистая (искусственная) шероховатость высотой k, при которой потери на трение равны соответствующим потерям при течении в рассматриваемой трубе с технической шероховатостью. Тогда считают, что величина данной технической шероховатости равна k.

Для стальных труб, не бывших в эксплуатации, k =(0.10¸0.15)мм; для чугунных труб, не бывших в эксплуатации, k =0.25 мм; для старых труб k ³0.5 мм. Помимо величины шероховатости k вводят понятие относительной шероховатости, выражаемой отношением k/d. Эта относительная величина полнее характеризует влияние шероховатости на потери напора.

При различных числах Рейнольдса шероховатость влияет на потери напора по-разному. Рассмотрим несколько различных случаев.

1). При ламинарном режиме движения жидкости шероховатость не влияет на сопротивление трения, так как все бугорки шероховатости, которые находятся в зоне малых скоростей у стенки, обтекаются плавно и коэффициент сопротивления трения зависит только от числа Рейнольдса

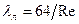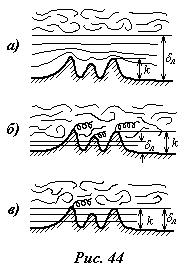
. (5.16)

В случае турбулентного потока, когда у стенок труб имеется ламинарный подслой, возможны три варианта обтекания бугорков шероховатости (рис.44).

2). При турбулентном течении, соответствующем Re <10⁵, толщина ламинарного подслоя значительна и d_л>>k, то есть все бугорки шероховатости находятся на дне ламинарного подслоя и обтекаются плавно, как при ламинарном течении (рис.44,а). При этом шероховатость не влияет на коэффициент сопротивления трения и он по-прежнему зависит только от числа Рейнольдса

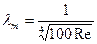. (5.17)

В этом случае говорят, что трубу можно считать гидравлически гладкой.

3). При течении с большими числами Рейнольдса возможен вариант, когда бугорки шероховатости выступают из ламинарного подслоя (d_л<<k) и обтекаются турбулентным потоком с образованием вихрей за каждым бугорком (рис.44,б). Тогда, за счет потерь энергии на образование вихрей, сопротивление потоку резко возрастает и коэффициент сопротивления зависит только от величины относительной шероховатости l_т=f (k/d):

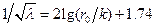, (5.18)

где r₀ – радиус трубы.

Такой режим называется режимом квадратичного сопротивления, так как l не зависит от числа Рейнольдса, а потери на трение (5.15) при этом получаются пропорцио-нальными квадрату скорости потока.

4). Возможен переходный режим течения между вторым и третьим вариантами, когда толщина ламинарного подслоя и высота бугорков – величины одного порядка, т. е. d_л@k (рис.44,в). Тогда коэффициент сопротивления зависит одновременно от обоих факторов l_т=f (Re, k/d):

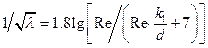, (5.19)

где k₁ – приведенная линейная характеристика шероховатости, приближенно равная 0.1*k.

Толщина ламинарного подслоя зависит от скорости потока в трубе. Следовательно, одна и та же труба с одной и той же шероховатостью может вести себя по-разному с точки зрения сопротивления трения, в зависимости от скорости потока и от соотношения k и d_л. При малых числах Рейнольдса труба может вести себя как гидравлически гладкая, а при больших – как шероховатая. В соответствии с этим понятия гладкой или шероховатой трубы являются чисто гидромеханическими, а не техническими.

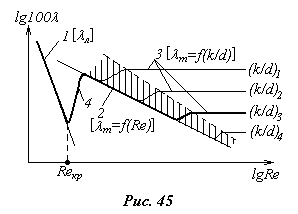
На рис.45 представлена зависимость l=f (Re,k/d). Линия 1 соответствует ламинарному движению l_л=f (Re), линия 2 – турбулентному движению в случае гидравлически гладкой трубы l_т=f (Re). Переход с кривой 1 на кривую 2 начинается при числе Рейнольдса, равном критическому Re_кр (кривая 4). Линии 3 характеризуют коэффициент сопротивления в зависимости от относительной шероховатости l_т=f (k/d). При этом, очевидно, что (k/d) ₁ >(k/d) ₂ >(k/d) ₃ >(k/d) ₄. В начале отхода от линии 2 все линии 3 на идут параллельно оси lgRe, т. е. в этой зоне, которая называется переходной (заштрихована), l_т=f (Re,k/d). За переходной зоной все линии 3 параллельны оси lgRe и здесь l_т=f (k/d). На рис.45 жирной линией показано изменение l в зависимости от Re для трубы с относительной шероховатостью (k/d) ₃.

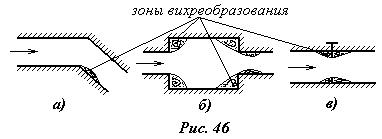
б) Потери напора на местные сопротивления или местные потери напора возникают в тех местах, где поток меняет свою конфигурацию или направление (участки с неплавно изменяющимся характером движения). К местным сопротивлениям относятся колена (рис.46,а), внезапное сужение или расширение потока (рис.46,б), различные краны, задвижки, фильтры, решетки (рис.46,в), и т. д. В этих случаях в потоке возникают вихри, которые главным образом и обусловливают потери энергии потока в местных сопротивлениях. Расчет местных потерь ведется по формуле

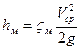, (5.20)

где z_м – коэффициент местного сопротивления, величина которого при достаточно больших числах Re зависит только от вида местного сопротивления (хотя в общем случае зависит также от числа Рейнольдса). Величина коэффициента местных потерь определяется, как правило, опытным путем и эмпирические (экспериментально полученные) формулы для различных видов местного сопротивления можно найти в соответствующих справочниках.

Дата добавления: 2014-01-05