Методы перестановки

Суть методов перестановки заключается в разделении исходного текста на блоки фиксированной длины и последующей перестановке символов внутри каждого блока по определенному алгоритму.

Перестановки получаются за счет разницы путей записи исходной информации и путей считывания зашифрованной информации в пределах геометрической фигуры. Примером простейшей перестановки является запись блока исходной информации в матрицу по строкам, а считывание по столбцам. Последовательность заполнения строк матрицы и считывания зашифрованной информации по столбцам может задаваться ключом. Криптостойкость метода зависит от длины блока (размерности матрицы). Так для блока длиной 64 символа (размерность матрицы 8x8) возможны 1,6x109 комбинаций ключа. Для блока длиной 256 символов (матрица размерностью 16x16) число возможных ключей достигает 1,4x1026. Решение задачи перебора ключей в последнем случае даже для современных ЭВМ представляет существенную сложность.

Перестановки используются также в методе, основанном на применении маршрутов Гамильтона, Этот метод реализуется путем выполнения следующих шагов.

Шаг 1. Исходная информация разбивается на блоки. Если длина шифруемой информации не кратна длине блока, то на свободные места последнего блока помещаются специальные служебные символы заполнители (например: *)

Шаг 2. Символами блока заполняется таблица, в которой для каждого порядкового номера символа в блоке отводится вполне определенное место (рис. 6).

Шаг 3. Считывание символов из таблицы осуществляется по одному из маршрутов. Увеличение числа маршрутов повышает криптостойкость шифра. Маршруты выбираются либо последовательно, либо их очередность задается ключом К.

Шаг 4. Зашифрованная последовательность символов разбивается на блоки фиксированной длины L. Величина L может отличаться от длины блоков, на которые разбивается исходная информация на шаге 1.

Расшифрование производится в обратном порядке. В соответствии с ключом выбирается маршрут и заполняется таблица согласно этому маршруту.

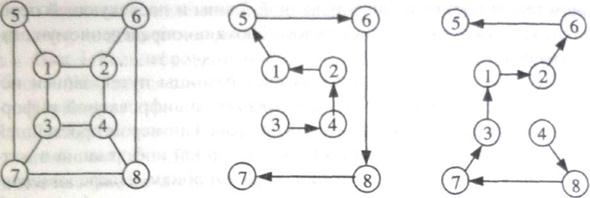
Таблица Маршрут № 1 Маршрут№2

Рис. 6. Вариант 8-элементной таблицы и маршрутов Гамильтона

Из таблицы символы считываются в порядке следования но-меров элементов. Ниже приводится пример шифрования информации с использованием маршрутов Гамильтона.

Пусть требуется зашифровать исходный текст То = <МЕТОДЫ_ПЕРЕСТАНОВКИ>. Ключ и длина зашифрованных блоков соответственно равны: К=<2,1,1>, L=4. Для шифрования используются таблица и два маршрута, представленные на рис. 6. Для заданных условий маршруты с заполненными матрицами имеют вид, показанный на рис. 7.

Дата добавления: 2014-01-05