Аналитические и графические (статистические) методы

Прикладные классификации МФПС

Классификации МФПС

Первоначально выделяли детерминированные и вероятностные классы моделей. Затем в самостоятельные классы выделились теоретико-множественные представления, графы, математическая логика и другие разделы.

По классификации Ф.Е.йТемникова [20] выделяют группы методов: аналитические (интегродифференциальное исчисление, методы поиска экстремумов, вариационное исчисление и др.); статистические; теоретико-множественные, логические, лингвистические, семиотические представления, составляющие основу разработки языков моделирования, автоматизации проектирования; графические (теория графов и разного рода графические представления информации).

В математике возникают новые направления "на пересечении" методов (комбинаторика - алгебра групп и теория множеств, топология - теоретико-множественные и графические представления, нечеткие формализации на основе размытых множеств и т. д.).

Практически невозможно создать единую классификацию, которая бы включала в себя все разделы современной математики.

На базе математических направлений развиваются прикладные методы и предлагают их классификации для решения практических задач.

Развитие автоматизированных систем сбора, хранения и обработки информации привело к появлению классификации, показанной в табл. 2.1.

Двухмерная классификация удобна тем, что в нее можно «входить» через прикладные направления (слева) и через математические (сверху).

Все методы современной математики не может глубоко знать ни один специалист. При выборе метода важно понимать его особенности и возможности использования. Выбрав метод, следует приглашать специалистов для решения задачи.

Таблица 2.1

Прикладные классификации методов моделирования	Классификации методов формализованного представления систем
Теоретико-множест-венные	Логи-ческие	Лингвис-тические	Графи-ческие
Методы организации массивов	+	+		+
Методы обработки массивов (сортировки, упорядочения, размещения)	+	+
Методы поиска информации	+	+	+

Эти методы получили наибольшее распространение в практике проектирования и управления.

В рассматриваемой классификации аналитическими называют те методы, которые отображают реальные процессы и объекты в виде точек, совершающих какие-либо перемещения в пространстве или взаимодействующих между собой.

Основу понятийного аппарата аналитических методов составляют понятия классической математики - величина, формула, функция, уравнение, система уравнений, логарифм, дифференциал, интеграл и т.д.

Дифференциальные уравнения. Непрерывно-детерминирован-ные модели, т.е. D-схемы, строятся на основе непрерывно-детерминистического подхода. Модель обычно выражается в аналитическом виде, в котором связываются функции выходных величин, входных и возмущающих воздействий. Наиболее часто при составлении моделей используется аппарат дифференциальных уравнений (ДУ). ДУ выводятся из конечно-разностных уравнений, которые составляются на основе анализа динамики физических изменений в объекте.

Пусть на вход динамической системы, характеризующейся вектором состояний 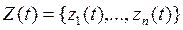, подаётся входной сигнал 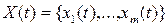, а с выхода снимается выходной сигнал 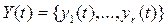. Тогда модель в виде обыкновенных ДУ в общем случае задаётся следующим соотношениями:

а) ДУ движения в пространстве состояний

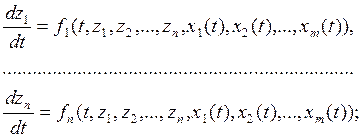(2.1)

б) соотношениями для входных сигналов

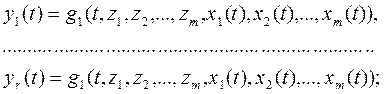(2.2)

в)Цначальными условиями при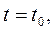

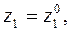
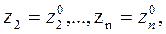
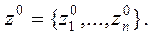
г) значениями входного процесса

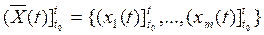
Решением системы уравнений (1.1) будет уравнение

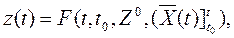
называемое функцией перехода, а решением системы (1.2) будет уравнение

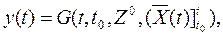
называемое функцией выходов динамической системы. Оба эти уравнения могут быть приняты в качестве математических моделей.

На основе аналитических представлений возникли и развиваются математические теории различной сложности - от математического анализа до математического программирования, теории игр и т.д.

Далеко не всегда символические представления классической математики адекватно отражают реальные сложные процессы, т.е. их нельзя считать строгими математическими моделями.

Большинство из направлений математики не содержит средств постановки задачи, и доказательство адекватности модели, которое доказывается экспериментом, по мере усложнения проблемы становится дорогостоящим и не бесспорным.

В состав этого класса методов входит математическое программирование [21], которое содержит средства постановки задачи и расширяет возможности доказательства адекватности модели.

Метод линейного программирования. Методы матема-тического программирования составляют раздел математики, в котором изучаются методы нахождения минимума или максимума функции конечного числа переменных при условии, что переменные удовлетворяют конечному числу дополнительных условий (ограничений), имеющих вид уравнений или неравенств. Различают линейное и нелинейное математическое программирование. Рассмотрим элементы линейного программирования (ЛП).

Линейным программированием называется раздел математики, в котором изучаются методы нахождения минимума или максимума линейной функции конечного числа переменных при условии, что переменные удовлетворяют конечному числу дополнительных ограничений, имеющих вид линейных уравнений или неравенств. Таким образом, задача линейного программирования (ЗЛП) в общем случае формулируется следующим образом: найти такие значения действительных переменных 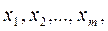для которых целевая функция

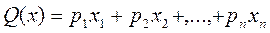
принимает минимальное значение на множестве точек, координаты которых удовлетворяют условиям

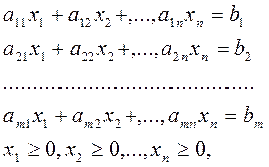
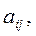
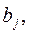
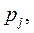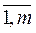где коэффициенты (i=, j=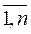) - действительные числа.

Можно предполагать, что

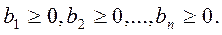
В матричном виде ЗЛП формулируется следующим образом:

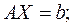
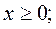
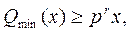
где 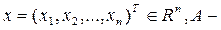матрица 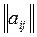размером ;

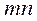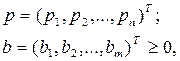
где 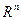- область возможных решений.

Если имеется максимум целевой функции

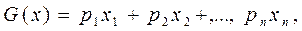
то это равнозначно отысканию минимума функции

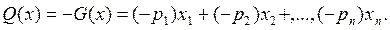
Если в дополнительных условиях имеется неравенство, например

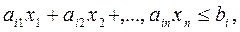
то вводом вспомогательного переменного множителя 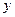можно перейти к уравнению

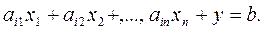
Для нового переменного также справедливо неравенство 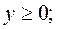в целевую функцию оно входит с коэффициентом .

Если для переменной 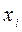не задано условие 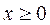, то могут быть введены, например, новые переменные 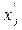и 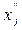с дополнительными условиями и 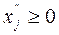, причем 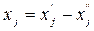. Поэтому в дальнейшем будем рассматривать в основном задачи минимизации целевой функции 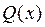при условиях, заданных линейными уравнениями с неотрицательными членами 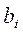в предположении неотрицательных переменных. Эти задачи будем называть ЗЛП. В математической литературе ЗЛП записывается в виде

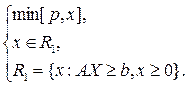(2.3)

Любая ЗЛП может быть приведена к виду (2.3). Двойственной к выражению (2.3) будем называть задачу

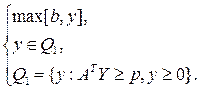
Точка 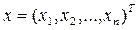, удовлетворяющая всем условиям, называется допустимой. Множество всех допустимых точек называется допустимой областью. Если после отбрасывания одного условия допустимая область не меняется, то такое условие называется лишним.

В задачах с двумя переменными можно отказаться от перехода от неравенств к уравнениям, так как линейное неравенство 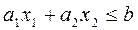допускает непосредственную геометрическую интерпретацию: все точки, удовлетворяющие этому неравенству, лежат на прямой 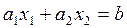и в одной из двух полуплоскостей, на которые эта прямая делит всю плоскость.

Множество всех оптимальных решений ЗЛП выпукло. Если допустимая область образована 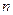неравенствам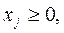и и 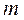уравнениями, то она может иметь самое большее 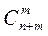вершин.

Если допустимая область ограничена и непуста, то она является выпуклым многогранником, и задача ЗЛП в этом случае всегда разрешима, а оптимальное значение целевой функции достигается, по крайней мере, в одной из вершин многогранника.

Если допустимая область пуста, то ЗЛП неразрешима.

Если допустимая область неограничена, то ЗЛП может быть разрешимой.

Канонический вид ЗЛП. Основным алгоритмом решения ЗЛП является симплекс-метод, его можно применять в том случае, когда ЗЛП задана в специальном каноническом виде.

Например, каноническая форма 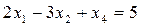, к которой может привести неравенство

,

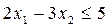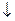
при .

Формулировка задачи представлена в виде

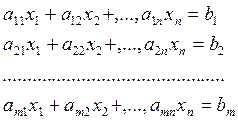
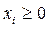
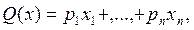
Если каждое из уравнений содержит одну переменную такую, что коэффициент перед ней в этом уравнении равен 1, а во всех других уравнениях равен 0, и если при этом все 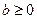, то говорят о допустимом каноническом виде. Переменные 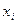называют базисными, а остальные - свободными.

Например,

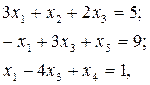
где 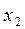, , 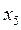- базисные переменные;

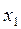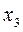, - свободные переменные.

В целевую функцию должны входить только свободные переменные.

Если целевая функция имеет вид

,

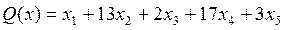то вычитанием из этого выражения первого уравнения, умноженного на 13 (так как там выделена переменная 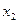, а в целевой функции 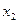имеет коэффициент 13), второго уравнения, умноженного на 3, и третьего - на 17, получим целевую функцию

.

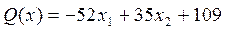Тогда окончательно ЗЛП в каноническом виде запишется так:

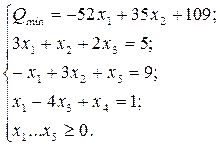(2.4)

При всех .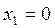

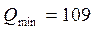Задача (2.4) решается симплекс-методом. Для этого находим базисное решение (2.4).

Так как ограничения в виде уравнений представляют собой плоскости в n -мерном пространстве, а также условия 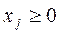, то решение ЗЛП ищется в вершинах образованного в n -мерном пространстве многогранника, который сам по себе представляет область допустимых решений.

Рассмотрим на примере особенности этого метода.

Пусть в цехах Ц1, Ц2, ЦЗ изготавливаются изделия И1 и И2. Известна загрузка в процентах каждого цеха а_i и прибыль с_i от реализации изделий. Данные сведены в табл. 2.2.

Таблица 2.2

Изделия	Цех (участок)	Цена
	Ц1	Ц2	Ц3	изделия
И1	5 %	1,6 %	2,9 %	240 руб.
И2	4 %	6,4 %	5,8 %	320 руб.
Максимальная загрузка	100 %	100 %	100 %

Необходимо определить, сколько изделий каждого вида следует производить при возможно большей загрузке цехов, чтобы получить за плановый период максимальную прибыль или максимальный объем реализуемой продукции.

Целевая функция имеет вид

F=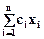=240 x₁+320 x₂ ® max, (2.5)

где x₁ и x₂ - искомые параметры.

Известны следующие ограничения:

5x₁+4x₂ £100, (2.6.а)

1,6x₁+6,4x₂ £100, (2.6.b)

2,9x₁+5,8x₂ £100, (2.6.c)

При условии однородности ограничений эти ограничения можно сформулировать в общем виде

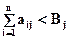. (2.7)

Графическое решение задачи приведено на рис. 2.3.

Рис. 2.3

На рис.2.3 показаны l₁, l₂, l₃, l₄, l₅ - линии, образуемые целевой функцией.

Ограничения определяют область допустимых решений, а наклон прямой, отображающий целевую функцию, определяет точку последнего ее пересечения с областью допустимых решений, которая и является наилучшим решением задачи (оптимумом) - x₁ =9, x₂=13.

Основные особенности математического программирования следующие.

Целевая функция и ограничения являются средствами постановки задачи.

Существует возможность объединения в одной модели разнородных критериев, что важно при отображении проектных и производственных ситуаций.

Модель математического программирования допускает выход на границу области определения переменных в отличие от методов классической математики.

Возможно построение пошагового алгоритма получения результатов моделирования.

Таким образом, аналитические методы применяются в том случае, когда свойства систем можно отобразить в виде детерминированных величин или зависимостей, т.е. когда знания о процессах и событиях в некотором интервале времени позволяют полностью определить поведение их вне этого интервала.

Основой статистических представлений явлений и процессов является их описание вероятностными характеристиками и стохастическими закономерностями.

Статистические закономерности представимы в виде дискретных случайных величин и их вероятностей или в виде непрерывных зависимостей распределения событий, процессов.

Для дискретных событий соотношение между возможными значениями случайной величины х_i и их вероятностями р_i называют законом распределения. Это может быть записано в виде ряда x₁«p₁, x₂«p₂,..., x_n«p_n, либо представляют в виде зависимостей F(x) или p_i(x_i).

Функция распределения вероятностей определится формулой

F(x)=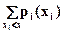 (2.8)

Для случайных непрерывных величин (процессов) закон распределения представляют либо в виде функции распределения вероятностей F(x), либо в виде плотности вероятностей р(х)=dF(x)/dx, DF(x)=р(х)Dx, где р(х) есть вероятность того, что случайная величина х принадлежит отрезку (x,x+Dx), или р(х)=P{хÎ(x,x+Dx)}.

Для полной группы несовместных событий выполняется условие нормирования закона распределения

F(x)=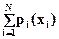=1 (2.9)

и плотности распределения вероятностей

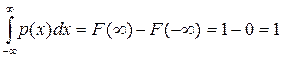(2.10)

Получение закона распределения представляет собой иногда трудную и невыполнимую задачу. Поэтому пользуются его характеристиками - начальными и центральными моментами.

Наибольшее распространение получили следующие моментные функции:

- первый начальный момент, или математическое ожидание, или среднее значение случайной величины, которое для дискретных величин определится по формуле

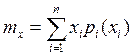, (2.11а)

для непрерывных величин определится по формуле

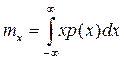; (2.11б);

-ввторой центральный момент, или дисперсия случайной величины, которая для дискретных величин определится по формуле

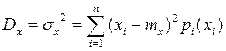, (2.12а)

а для непрерывных величин определится по формуле

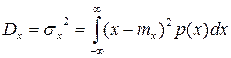. (2.12б)

На практике иногда применяют среднее квадратическое отклонение s_x.

Связь между системами характеризуется ковариацией, или моментом связи. Для двумерного распределения момент связи имеет запись cov(x,y), или m_xy, или М[(х–m_x)(у–m_y)].

Применяют ковариацию нормированных отклонений, или коэффициент корреляции, который определится по формуле

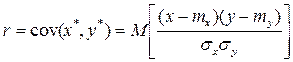, (2.13)

где x^*=(х–m_x)/s_x, y^*=(у–m_y)/s_y - нормированные отклонения.

Доказательства адекватности статистических закономерностей базируется на понятии выборки.

Под выборкой понимается часть изучаемой совокупности явлений, на основе которой получают статистические закономерности, присущие всей совокупности и распространяемые на нее с какой-то вероятностью.

На базе статистических представлений развиты математические теории: математическая статистика [5, 22, 23], теория статистических испытаний, теория статистического имитационного моделирования, теория выдвижения и проверки статистических гипотез, теория статистических решающих функций, теория потенциальной помехоустойчивости, статистическая радиотехника, статистическая теория распознавания образов, экономическая статистика, теория массового обслуживания; стохастическое программирование и т. п.

Дата добавления: 2014-01-05