Лингвистические, семиотические представления

Семиотика возникла как наука о знаках, знаковых системах.

Основными понятиями, на которых базируются семиотические представления, являются понятия: тезаурус, грамматика, семантика, прагматика.

Термин тезаурус (богатство, клад, запас и т. д.) используется для характеристики конкретного языка, его многоуровневой структуры и определяется как "множества смысловыражающих элементов языка с заданными смысловыми отношениями"[28].

На рис. 2.7 представлена структура языка в виде уровней (страт) множеств (слов, словосочетаний, предложений, абзацев и т. п.), смысловыражающие элементы каждого из которых формируются из смысловыражающих элементов предшествующих структурных уровней.

Рис.2.7

Правила G1 и G2 формирования смысловыражающих элементов в тезаурус не входят, в тезаурусе определяется только вид и наименование уровня, характер и вид смысловыражающих элементов.

Понятие тезауруса используется при создании искусственных языков - языков моделирования, автоматизации проектирования, информационно-поисковых языков.

Под грамматикой понимаются правила, с помощью которых формируются смысловыражающие элементы языка. Пользуясь этими правилами, можно порождать грамматически (синтаксически) правильные конструкции или распознавать их грамматическую правильность.

Под семантикой понимается содержание, значение, смысл формируемых или распознаваемых конструкций языка.

Под прагматикой понимается полезность для данной цели, задачи.

В естественном языке различить понятия терминов «семантика» и «прагматика» трудно. Обычно это делается при парном представлении терминов:

<семантика>: =<содержание>|<смысл>|<значение>;

<прагматика>:=<смысл>|<значение>|<полезность;>

Эти понятия рассматривают на примерах.

Пример синтаксической правильности и семантической бессмысленности: «Глокая куздра тщето борзуданула бокра и курдычет бокрёнка» или «Муха лукаво всплеснула зубами».

Пример прагматически неправильного предложения для директора завода: «Маленькая девочка собирает цветы на лугу».

Пример прагматически правильного предложения для того же директора: «Слесарь Иванов собирает цветы на лугу».

При создании и использовании искусственных языков применяют такие понятия структурной лингвистики, как порождающая и распознающая грамматика.

Под порождающей грамматикой понимается совокупность правил, с помощью которых обеспечивается возможность формирования из первичных элементов (словаря) синтаксически правильных конструкций.

Под распознающей грамматикой понимаются правила, с помощью которых обеспечивается возможность распознавания синтаксической правильности предложений, фраз или других фрагментов языка.

Классы формальных грамматик являются основой теории формальных языков.

Формальный язык определяют как множество предложений (или “цепочек”), каждое из которых имеет конечную длину и построено с помощью некоторых операций (правил) из конечного множества элементов (символов), составляющих алфавит языка.

Формальную грамматику определяют в виде четверки множеств [28]:

G = <V_T,V_N,R,A>, (2.21)

где V_T - множество основных (терминальных) символов; V_N - множество вспомогательных (нетерминальных) символов; R - множество правил вывода, или продукций, которые могут иметь вид:

a®b, (2.22)

т.е. bÎV_TÈV_N - цепочка из терминальных и нетерминальных символов множеств V_T и V_N, а aÎ(V_TÈV_N)V_N(V_TÈV_N), т.е. a - цепочка из терминальных и нетерминальных символов, содержащая, по крайней мере, один нетерминальный символ из V_N; A - множество аксиом.

Рассмотрим пример порождающей грамматики.

Пусть даны V_T =<в₁,в₂,п,л>, V_N=<S,P>. Заданы порождающая и распознающая грамматики следующего вида:

Порождающая грамматика:

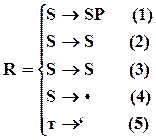
Распознающая грамматика:

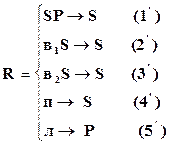
Применяя правила R в приведенной последовательности. получим:

S Þ SP Þ в₁SP Þ в₁в₂SP Þ в₁в₂nP Þ в₁в₂nл.

(1) (2) (3) (4) (5)

Пусть терминальные символы V_N имеют следующую расшифровку: в₁ - «все», в₂ - «возрасты», п - «покорны», л - «любви».

Тогда полученное предложение «в₁в₂пл» - «все возрасты покорны любви».

Если изменить последовательность применения правил, то будут получаться другие предложения.

Последовательность (1)Þ(3)Þ(2)Þ(4)Þ(5) - «возрасты все покорны любви».

Если применить не все правила (1)Þ(2)Þ(4)Þ(5) - «все покорны любви».

А для получения фразы «любви все возрасты покорны» надо изменить первое правило: вместо S®SP включить в R правило SÞPS.

Следовательно, вид порождаемых цепочек зависит от вида правил (исчисления) и от последовательности их применения (алгоритма).

Распознающая грамматика для рассматриваемого примера будет содержать как бы «перевернутые» правила, которые применяются в обратной последовательности.

На рис.2.8 приведен пример анализа правильности предложения с помощью правил распознающей грамматики.

Рис.2.8

Подобным образом можно моделировать порождение деловых писем или других документов, имеющих формализованный стиль и формальную структуру.

Можно создавать языки моделирования структур, языки автоматизации проектирования сложных устройств и систем.

Семиотические представления пользуются другими по сравнению с математической лингвистикой средствами исследования семантических возможностей языков, например, понятием треугольника Фреге [28, 29], согласно которому любой знак имеет форму, синтаксис (означаемое знака) и семантику (смысл, значение).

На границе лингвистики и семиотики возникли языки синтагматического типа, использующие правила {a_i,r_k,b_j}, называемые синтагмой, где a_iÎА, b_jÎВ - взаимодействующие множества исходных понятий языка; r_kÎR - множества отношений, которые могут иметь произвольный вид.

Для конкретизации отношений R используются отношения эквивалентности, толерантности и строгого порядка, свойства которых сведены в табл. 2.5.

Таблица 2.5

	Свойство
Отношение	Рефлексивность	Симметричность	Транзитивность
Эквивалентность Толерантность Строгий порядок	+ + -	+ + -	+ - +

Рассмотрим пример применения отношения толерантности.

Толерантность - такой вид сходства, при котором сопоставляемые элементы находятся в отношении, обладающем рефлексивностью и симметричностью, но не обладающем транзитивностью. Тогда, если при сопоставлении слов ввести допустимую ошибку в один символ, то отношение сходства между первым и вторым словами может быть признано (с точностью до допустимой ошибки) рефлексивным и симметричным; аналогично - между вторым и третьим; но первое и третье слова уже могут отличаться не одним, а двумя символами, и сходство между ними можно вообще не обнаружить, т.е. не будет выполнено отношение транзитивности.

С помощью отношения толерантности можно отобразить некоторые отношения между словами естественного языка. Например:

Дата добавления: 2014-01-05