Общие положения. Поверхности вращения

Поверхности вращения

Поверхностью вращения называется поверхности образованная вращением какой-либо линии вокруг неподвижной прямой, называемой осью.

Образующая может быть как плоской, так и пространственной кривой. til гак, для задания поверхности вращения необходимо задать ось / и образующую определитель поверхности - <P(i\a)[A] (рис. 3.31, а)

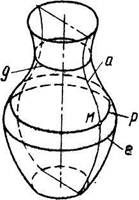
		Каждая точка образующей линии а описывает окружность р - параллель шшерхности. Наибольшая из параллелей называется экватором, наименьшая - мрлом g. Кривые /я, лежащие в сечении поверхности вращения плоскостями, ^юходящими через ось /, называются меридианами. Итак, поверхность враще-*шя несет на себе два семейства линий - параллели и меридианы. Параллели поверхности вращения подобны, а меридианы равны между coбой. Любая меридиальная плоскость является плоскостью симметрии по&ерхно^ I >.г,\ а сам меридиан представляет собой кривую, симметричную в?№ё№йпта оси I м, пвдения. Каркас поверхности вращения может быть
Рис. 3.31

составляй из параллелей и I •" ридианов. Поверхность вращения может быть задана на чертеже прозкшши племен* I» i I ее определителя, т. е. оси и образующей (рис. 3.31, б). Выберем ось / - герн* I <гально*п|5оецирующую прямую, а образующую плоскую кривую а, лежащую и

1^жэо«тально-проецирующей плоскости рфн)«Убедимся, что поверхность зада­на на чертеже. Для этого необходимо проверить, можно ли по одной проекции точки М{М\ лежащей на поверхности, построить недостающую проекцию. Вос­пользуемся параллелью, проходящей через точку Л/, ее горизонтальная проекция р\ Отметим точку ЛХК\Л?")пересечения параллели с образующей а. Параллель проецируется на горизонтальную плоскость проекций без искажения, так как ось / перпендикулярна плоскости Я, а на фронтальную плоскость в отрезок прямой, перпендикулярный /".

Поверхность вращения очень часто задается на чертеже проекцией мери­диана, лежащего во фронтальной плоскости, такой меридиан называется главным, и проекцией оси. \

Главный меридиан т является очертанием поверхности на плоскость ^Я Для построения его точек (рис. 3.31, б) необходимо повернуть точки образующей Я а вокруг оси / до их совпадения с плоскостью у(у_н) главного меридиана. Точки Я будут перемещаться по параллелям, т. е. на И - по окружностям, а на V — по пря­мым, перпендикулярным линиям связи.

На чертеже теперь видим проекцию поверхности вращения - определитель, главный меридиан, верхнюю и нижнюю параллель.

Дата добавления: 2014-01-05