
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие о чистом сдвиге. Напряжения и деформации при сдвиге. Закон Гука
|
|
|
|
На примере растяжения и сжатия были выявлены некоторые наиболее важные свойства напряженного состояния. При растяжении в зависимости от ориентации секущей площадки на гранях выделяемой площадки возникают как нормальные, так и касательные напряжения.
Теперь положим, что имеется такое напряженное состояние, когда на гранях возникают только касательные напряжения 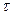 . Такое напряженное состояние называется чистым сдвигом (рис.3.1).
. Такое напряженное состояние называется чистым сдвигом (рис.3.1).
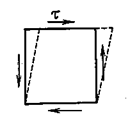
Рис. 3.1
Посмотрим, как при чистом сдвиге изменяются напряжения в зависимости от ориентации секущей площадки.
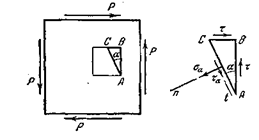

Рис. 3.2
Для этого из пластин, находящихся в состоянии чистого сдвига, выделим элементарную трехгранную призму  (рис. 3.2).
(рис. 3.2).
На гранях  и
и  по условию возникают только касательные напряжения. На грани
по условию возникают только касательные напряжения. На грани  в зависимости от угла возможно возникновение как нормального, так и касательного напряжения. Обозначим их через
в зависимости от угла возможно возникновение как нормального, так и касательного напряжения. Обозначим их через 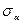 и
и 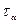 . Спроектируем все силы на оси n и t.
. Спроектируем все силы на оси n и t.
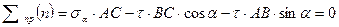
 ,
,
т.к.  и
и  то,
то,
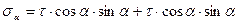
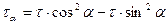


В результате получим
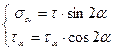 (3.1)
(3.1)
При 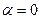 и
и 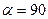
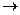
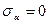 а
а 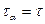 , что соответствует исходным площадкам. При
, что соответствует исходным площадкам. При 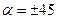
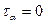 , а
, а 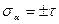 .
.
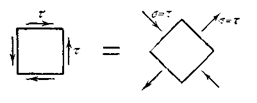
|
Следовательно, если выделить прямоугольный элемент грани, который повернут на 450 относительно исходных, то на секущих площадках будут обнаружены только нормальные напряжения, причем на одной паре граней эти напряжения являются растягивающими, а на другой сжимающими. Таким образом, чистый сдвиг может быть представлен как одновременное растяжение и сжатие по двум взаимно перпендикулярным направлениям (рис. 3.3).
Рис. 3.3
Рассмотрим деформацию элемента ограниченного площадками чистого сдвига (рис. 3.4).
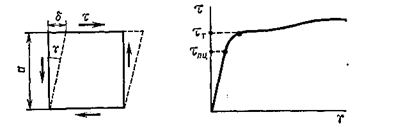
Рис. 3.4
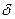 — абсолютный сдвиг
— абсолютный сдвиг
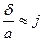 — относительный сдвиг или угол сдвига.
— относительный сдвиг или угол сдвига.
Величина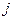 , как показывают эксперименты в пределах напряжений пропорциональности, прямо пропорциональны величине касательных напряжений. Эта зависимость между
, как показывают эксперименты в пределах напряжений пропорциональности, прямо пропорциональны величине касательных напряжений. Эта зависимость между 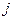 и
и 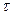 , называется законом Гука при сдвиге, выражается в виде
, называется законом Гука при сдвиге, выражается в виде
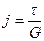 или
или 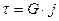 ,где (3.2)
,где (3.2)
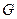 — модуль сдвига или модуль упругости второго рода.
— модуль сдвига или модуль упругости второго рода. 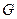 имеет раз-мерность напряжения (для стали Ст.3
имеет раз-мерность напряжения (для стали Ст.3 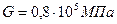 ).
).

Между  и
и 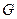 существует зависимость
существует зависимость 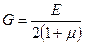 . Данная формула показывает, что три постоянных
. Данная формула показывает, что три постоянных 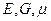 — характерные упругие свойства изотропного материала связаны между собой.
— характерные упругие свойства изотропного материала связаны между собой.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1739; Нарушение авторских прав?; Мы поможем в написании вашей работы!