
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Использование свойств симметрии при раскрытии статической неопределенности
|
|
|
|
Пусть имеется симметричная в геометрическом смысле рама (рис. 7.6), т.е. левая часть является зеркальным отображением правой части относительно оси симметрии. При расчете таких систем решение канонических уравнений можно упростить.

Рис. 7.6
Рассмотрим два случая загружения рамы: симметричной (рис. 7.6, б) и кососимметричной (рис. 7.6, в) нагрузкой. Аналогично будем классифицировать и внутренние силовые факторы. Рассекая стержень в общем случае нагружения, будем иметь шесть составляющих внутренних усилий.
Докажем следующее положение: у симметричной рамы при симметричной нагрузке обращаются в нуль, кососимметричные неизвестные, а при кососимметричной нагрузке — симметричные неизвестны.

Рис. 7.7
Рассмотрим раму, изображенную на рис. 7.6. Основная система при использовании свойств симметрии должна быть обязательно симметричной. Она будет общей как при симметричном, так и кососимметричном загружении. На рисунке 7.8 показаны основная и эквивалентные системы.

Рис. 7.8
Обозначая через 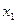 и
и 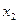 — кососимметричные силовые факторы, и через
— кососимметричные силовые факторы, и через  и
и 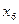 симметричные, выпишем систему канонических уравнений. В данном случае их будет шесть:
симметричные, выпишем систему канонических уравнений. В данном случае их будет шесть:
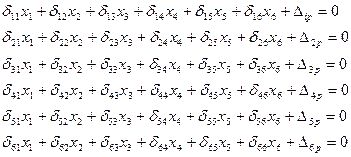
Заменим теперь, что в этих уравнениях многие из коэффициентов обращаются в нуль. Это будут все коэффициенты, у которых один индекс принадлежит симметричному, а другой — кососимметричному фактору. Например, обращается в нуль коэффициент  . Индекс 1 принадлежит кососимметричному фактору, а индекс 3 — симметричному фактору. Обращаются также в нуль
. Индекс 1 принадлежит кососимметричному фактору, а индекс 3 — симметричному фактору. Обращаются также в нуль 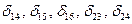 и т.д. Сказанное становится более очевидным, если учесть, что в рассматриваемой системе эпюра изгибающих моментов от кососимметричных факторов будет кососимметричной, а от симметричных факторов — симметричной. При перемножении таких эпюр, естественно получим нуль, в то время как перемножение кососимметричной эпюры на кососимметричную и симметричной на симметричную дает результат, отличный от нуля.
и т.д. Сказанное становится более очевидным, если учесть, что в рассматриваемой системе эпюра изгибающих моментов от кососимметричных факторов будет кососимметричной, а от симметричных факторов — симметричной. При перемножении таких эпюр, естественно получим нуль, в то время как перемножение кососимметричной эпюры на кососимметричную и симметричной на симметричную дает результат, отличный от нуля.
Вычеркивая из системы уравнений коэффициенты, обращающиеся в нуль, получим:


Как видим, система уравнений распалась на две независимые.
Теперь положим, что внешняя нагрузка является симметричной. Из сказанных выше соображений следует, что  . Первая система уравнений становится однородной. Тогда
. Первая система уравнений становится однородной. Тогда 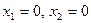 . Следовательно, при симметричной нагрузке кососимметричные силовые факторы обращаются в нуль.
. Следовательно, при симметричной нагрузке кососимметричные силовые факторы обращаются в нуль.
При кососимметричной нагрузке  . Тогда
. Тогда  . В этом случае в плоскости симметрии обращаются в нуль симметричные силовые факторы.
. В этом случае в плоскости симметрии обращаются в нуль симметричные силовые факторы.
Таким образом, при симметричной нагрузке кососимметричные неизвестные равны нулю, а при кососимметричной нагрузке —симметричные раны нулю. Если внешняя нагрузка не обладает свойствами симметрии, то ее всегда можно разложить на симметричную и кососимметричную, как показано на рис. 7.9.
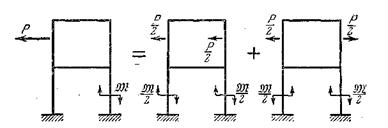
Рис. 7.9
При этом задача распадается на две, которые решаются отдельно. Окончательные эпюры получаются сложением эпюр от симметричной и кососимметричной нагрузки.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 382; Нарушение авторских прав?; Мы поможем в написании вашей работы!