Главные оси и главные напряжения. Рассмотрим два вида напряженных состояний:

Рассмотрим два вида напряженных состояний:

а) объемное напряженное состояние

В каждой точке тела существуют также три взаимно- перпендикулярные площадки (главные), на которых действуют только нормальные напряжения, называемые главными.

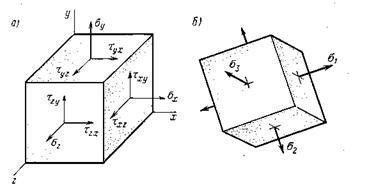
Рис. 9.4

На рис. 9.4,а элемент, вырезанный произвольными площадками, на рис. 9.4,б — главными площадками.

Предположим, что наклонная площадка является главной, тогда на ней будет действовать только нормальное напряжение 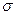(рис. 9.5).

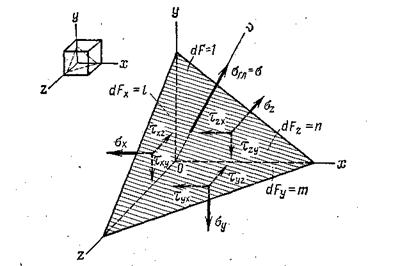
Рис. 9.5

Проекции 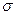на координатные оси равны

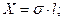
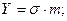
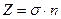(9.2)

Приравнивая 9.2 и 9.1, получим:

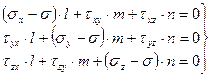(9.3)

Получаем систему трех алгебраических уравнений относительно направляющих косинусов 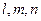. Причем известно, что 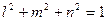. Значит одновременно 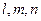не могут быть равны нулю. Поэтому система (9.3) имеет решение отличное от нуля. Система алгебраических уравнений имеет решение отличное от нуля, если определитель из ее коэффициентов равен нулю.

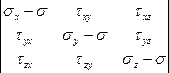= 0 (9.4)

Раскрывая определитель (9.4) получим кубическое уравнение относительно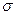

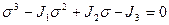, (9.5)

где 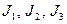— коэффициенты кубического уравнения и определяются следующими соотношениями

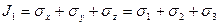
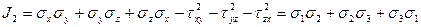
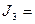
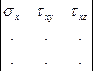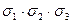= (9.6)

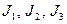— называются первым, вторым, третьим инвариантом напряженного состояния. Решив кубическое уравнение, получим три действительных корня 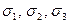. После того как найдены 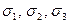, их переномеровывают согласно неравенству

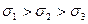. (9.7)

б) частный случай, когда одна из площадок является главной (рис. 9.6).

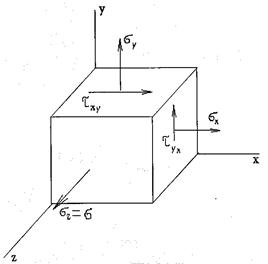
Рис. 9.6

В этом случае 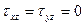. При подстановке их в определитель (9.5) он распадается на два определителя второго порядка и первого:

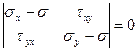
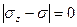(9.8)

Последний определитель сразу дает главный корень 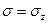. Раскрывая второй определитель второго порядка: имеем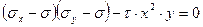

или .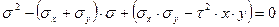

Получим квадратное уравнение для нахождения остальных двух корней. Его решение имеет вид

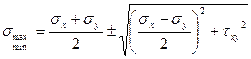(9.9)

Таким образом, если одна из площадей главная, то один корень известен 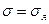, а два других находятся по формуле (9.9).

Дата добавления: 2014-01-05