Теория пластичности и разрушения Мора

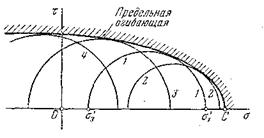
Допустим, что мы можем провести опыт при любом напряженном состоянии с пропорциональным изменением всех компонентов тензора напряжений. Выберем некоторое напряженное состояние, и будем пропорционально увеличивать все компоненты, пока напряженное состояние не станет предельным. В образце либо появятся пластические деформации, либо он разрушится. Вычертим на плоскости наибольший из кругов Мора. Будем считать, что предельное состояние не зависит от 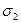. Взяв, далее, новые напряженные состояния построим круги 2, 3, 4 ……… Вычертим общую огибающую (рис. 10.6).

Рис. 10.6

Примем, что эта огибающая является единственной для данного материала. Если огибающая задана, то можно при любом напряженном состоянии установить коэффициент запаса. В этом подходе, не было принято ни каких гипотез и теория Мора основана по логической систематизации результатов опытов.

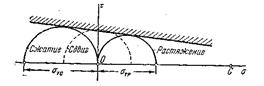
Теперь построим огибающую по минимальному числу опытов. Наиболее простыми являются испытания на растяжение и сжатие. Два предельных круга построены на рис. 10.7.

Рис. 10.7

Для определения огибающей важно найти т. , соответствующую трехосному равномерному растяжению. До сих пор нет метода, по определению этой точки экспериментальным путем. Вообще не удается провести опыты, когда все три главных напряжения являются растягивающими. Поэтому пока не удается построить для материала предельный круг, расположенный правее предельного круга растяжения. Сейчас огибающую аппроксимируют касательной к двум предельным кругам растяжения и сжатия. Когда будет возможность осуществлять всестороннее растяжение форму можно уточнить (рис. 10.8).

Рис. 10.8

Связь между напряжениям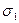и и 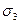для огибающей прямой можно представить в виде

(10.1)

Найдем коэффициент 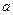и 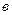воспользовавшись предельными кругами растяжения и сжатия.

При растяжении 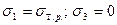подставляя в 10.1 найдем

, .

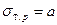При сжатии

.

Таким образом:

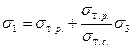
Или окончательно получим

Глава 11. ПРОЧНОСТЬ МАТЕРИАЛОВ ПРИ ЦИКЛИЧЕСКИ ИЗМЕНЯЮЩИХСЯ НАПРЯЖЕНИЯХ

Дата добавления: 2014-01-05