
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение качества задачи оценивания измеряемого параметра
|
|
|
|
Необходимыми компонентами математической постановки задачи оценивания измеряемых параметров являются: математическая модель измерения (ММИ); априорная и апостериорная информация; критерий оптимизации, а также ограничения, накладываемые на алгоритм оценивания вектора x и обеспечивающие его практическую реализуемость [3, 88].
При редукции экспериментальных данных возникает не только задача о точности или согласованности результатам измерения y модели, принятой в математической постановке задачи оценивания, но и задача возможности ее использования при редукции экспериментальных данных y. Надежность решения каждой из этих задач должна характеризоваться соответствующим риском [1]. Риск позволяет контролировать весь процесс интерпретации результатов измерения, включая диалог с оператором и вычисления на ЭВМ. В режиме диалога можно изменять и дополнять модель, основываясь на дополнительной информации по результатам редукции измерения, привлекать дополнительные измерения, т.е. риск формируемой в диалоге модели позволяет контролировать непротиворечивость привлекаемой информации и результата эксперимента.
Вычислительные погрешности, возникающие при редукции, влияют на совокупную надежность примерно так же, как погрешности в модели, привлекаемой для интерпретации. При этом критерием качества принимаемого решения выбирается риск [1, 76, 102], поскольку в используемом в этом случае апостериорном подходе основной характеристикой процедуры статистического вывода служит величина средних потерь среди тех экспериментов, которые закончились принятием одного и того же решения из пространства асимптотических решений [98].
В общем случае, для оценки надежности результатов измерения в темпе поступления измеряемой информации Y  , количественной мерой потерь от принятия оценки
, количественной мерой потерь от принятия оценки  вместо истинного значения x является функция потерь L (х,
вместо истинного значения x является функция потерь L (х,  (Y 0
(Y 0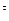 )) [1, 83, 98], которая определяется разницей (х –
)) [1, 83, 98], которая определяется разницей (х –  )и выборкой Y
)и выборкой Y  . При этом оценка
. При этом оценка  не совпадает, за редким исключением, с истинным значением случайного процесса х. Поскольку наблюдения у несут в себе элементы случайности, то случайными будут и значения L (х,
не совпадает, за редким исключением, с истинным значением случайного процесса х. Поскольку наблюдения у несут в себе элементы случайности, то случайными будут и значения L (х,  (Y 0
(Y 0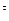 )), поэтому для построения функционала
)), поэтому для построения функционала  (Y
(Y  ) усредняют ее по множеству изменения процесса у
) усредняют ее по множеству изменения процесса у 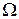 у:
у:
r (х,  ) = Мy [ L (х,
) = Мy [ L (х,  (Y
(Y  ))| х ] =
))| х ] = (х,
(х,  (Y
(Y  )) p (Y
)) p (Y  | x) dY
| x) dY  , (2.1)
, (2.1)
где p (Y  | х) – условная плотность распределения вероятностей.
| х) – условная плотность распределения вероятностей.
Оценку  в выражении (2.1) выбирают так, чтобы она соответствовала среднему значению х на множестве
в выражении (2.1) выбирают так, чтобы она соответствовала среднему значению х на множестве 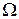 x, найденному с учетом вероятности появлений каждого значения х. Для этого используется средний риск – математическое ожидание условного риска r (х,
x, найденному с учетом вероятности появлений каждого значения х. Для этого используется средний риск – математическое ожидание условного риска r (х,  ), взятое по х:
), взятое по х:
R ( ) = М хr (х,
) = М хr (х,  ) =
) = (х,
(х,  ) p (x) dх, (2.2)
) p (x) dх, (2.2)
а критерием оптимизации оценивания выбирается критерий Байеса:
 R (
R ( ) = R (
) = R ( б). (2.3)
б). (2.3)
Из равенства (2.2) следует, что для квадратичной функции потерь
R (px,  | Y
| Y  ) =
) =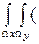 х –
х –  )2 p (x | Y
)2 p (x | Y  ) p (x) dх dY
) p (x) dх dY  .
.
Для минимизации риска выбранной модели используют наиболее распространенный метод получения точечных оценок – метод максимального правдоподобия [1, 2], заключающийся в нахождении решающего правила  (y) при Rn ®W x, для которого любой y максимизирует по x значение плотности вероятности p (y | x):
(y) при Rn ®W x, для которого любой y максимизирует по x значение плотности вероятности p (y | x):
p (y;  (y)) ³ p (y; x) для всех x Î W x. (2.4)
(y)) ³ p (y; x) для всех x Î W x. (2.4)
Статистика  (Y), которая удовлетворяет соотношению (2.4.), является оценкой максимального правдоподобия параметра x. В соответствие с принципом максимального правдоподобия, реализовавшееся на экспериментальной реализации х вектора наблюдений Y значение оценки максимального правдоподобия
(Y), которая удовлетворяет соотношению (2.4.), является оценкой максимального правдоподобия параметра x. В соответствие с принципом максимального правдоподобия, реализовавшееся на экспериментальной реализации х вектора наблюдений Y значение оценки максимального правдоподобия  (Y) принимается за приближенное значение неизвестного параметра x. В терминах
(Y) принимается за приближенное значение неизвестного параметра x. В терминах  (Y) и L (Y; x) соотношение (2.4) эквивалентно тому, что с вероятностью Р = 1
(Y) и L (Y; x) соотношение (2.4) эквивалентно тому, что с вероятностью Р = 1
L (Y;  (Y)) =
(Y)) = 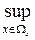 L (Y; x). (2.5)
L (Y; x). (2.5)
Соотношение (2.5) и объясняет происхождение термина «оценка максимального правдоподобия». При регулярном семействе P = { p (y; x), x Î W x }, для определения оценки максимального правдоподобия  (Y), находят решение уравнения правдоподобия
(Y), находят решение уравнения правдоподобия 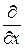 L (Y; x) = 0. Поскольку для любой положительной функции g (x) и функции ln g (x) экстремумы совпадают, то решают уравнение
L (Y; x) = 0. Поскольку для любой положительной функции g (x) и функции ln g (x) экстремумы совпадают, то решают уравнение
L(Y; x) = 0, (2.6)
где L(Y; x) = 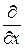 ln L (Y; x) – информант вектора Y.
ln L (Y; x) – информант вектора Y.
В соответствии с выражением (2.4), может существовать не одна, а несколько оценок максимального правдоподобия параметра x, что встречается в нерегулярных случаях, т. е. либо L (Y; x) не является дифференцируемой, либо множество Г(y) = { y: p (y; x) = 0} зависит от y. Поиск таких оценок становится труднее, но они обычно являются более точными в смысле минимизации квадратичного риска, поскольку из множества W x выделяются точки с нарушенными условиями регулярности, что является информацией о плотности f (y; x) вектора наблюдений Y.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 234; Нарушение авторских прав?; Мы поможем в написании вашей работы!