
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общий анализ алгоритмов оценивания по критерию минимума риска
|
|
|
|
Осуществленная формализация задачи последовательной минимизации риска оценки параметра измерения, позволяет сформулировать алгоритм определения минимума риска при условии анализа данных в режиме реального времени. При этом, по сравнению со статическим планом, среднее число экспериментов в рамках данного алгоритма может быть в несколько раз меньше при тех же малых вероятностях ошибок, то есть данный алгоритм обладает высокой эффективностью.
Если значение оценки  0 задается с точностью до неизвестного параметра g, то есть
0 задается с точностью до неизвестного параметра g, то есть  0 =
0 =  0(y, g), и для этой оценки достигается минимум апостериорного риска
0(y, g), и для этой оценки достигается минимум апостериорного риска
R ( 0(y, g), u, g) =
0(y, g), u, g) = 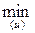 R (
R ( , y, g), (3.1)
, y, g), (3.1)
который не зависит от величины g, то априорная неопределенность в данной оценке не является существенной, а правило решения  0(y) является равномерно наилучшим правилом решения. В любой конкретной задаче с априорной неопределенностью следует проверить, решив уравнение (3.1), существует или нет равномерно наилучшее решение. Если априорная неопределенность является существенной, то решение уравнения (3.1) зависит от параметра g и представляет собой функцию
0(y) является равномерно наилучшим правилом решения. В любой конкретной задаче с априорной неопределенностью следует проверить, решив уравнение (3.1), существует или нет равномерно наилучшее решение. Если априорная неопределенность является существенной, то решение уравнения (3.1) зависит от параметра g и представляет собой функцию  0(y, g), описывающую оптимальное байесово правило решения для заданного значения g.
0(y, g), описывающую оптимальное байесово правило решения для заданного значения g.
Для получения рекуррентного выражения для оценки, рассмотрим величину среднего риска для правила решения  0(y,
0(y,  ) при значении g
) при значении g
R ( 0(y,
0(y,  ), g) =
), g) =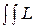 (
( 0(y,
0(y,  ), x, y) p (y, x |g) dxdy
), x, y) p (y, x |g) dxdy
и сравним ее с величиной среднего риска для оптимального байесова решения  0(x, g) при том же значении g
0(x, g) при том же значении g
R 0( 0(y, g), g) =
0(y, g), g) =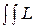 (
( 0(y, g), x) p (y, x |g) dxdy.
0(y, g), x) p (y, x |g) dxdy.
Для этого составим разность
D R ( , g) = R (
, g) = R ( 0(y,
0(y,  ), g) – R 0(
), g) – R 0( 0(y, g), g) =
0(y, g), g) =
= (
( 0(y,
0(y,  ), x) – L (
), x) – L ( 0(y, g), x)] p (y, x |g) dxdy =
0(y, g), x)] p (y, x |g) dxdy =
=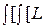 (
( 0(y,
0(y, ), x)– L (
), x)– L ( 0(y,g), x)] p (x | y,g) dx ] P (y |g) dy=
0(y,g), x)] p (x | y,g) dx ] P (y |g) dy= 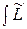 (
( ,g, y) P (y |g) dy, (3.2)
,g, y) P (y |g) dy, (3.2)
где
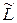 (
( , g, y) =
, g, y) = 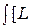 (
( 0(y,
0(y,  ), x) – L (
), x) – L ( 0(y, g), x)] p (x | y, g) dx. (3.3)
0(y, g), x)] p (x | y, g) dx. (3.3)
Разность D R ( , g) должна быть неотрицательна, поскольку при любом значении g правило решения
, g) должна быть неотрицательна, поскольку при любом значении g правило решения  (y, g) минимизирует величину среднего риска. Функция
(y, g) минимизирует величину среднего риска. Функция 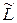 (
( , g, y) из равенства (3. 3) также неотрицательна, поскольку при любых значениях y и g она представляет собой разность значений апостериорного риска для двух решений
, g, y) из равенства (3. 3) также неотрицательна, поскольку при любых значениях y и g она представляет собой разность значений апостериорного риска для двух решений  1 =
1 =  0(y,
0(y,  ) и
) и  2 =
2 =  0(y, g), а именно второе решение соответствует минимальному значению апостериорного риска. При этом величина D R (
0(y, g), а именно второе решение соответствует минимальному значению апостериорного риска. При этом величина D R ( , g) и
, g) и 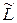 (
( , g, y) удовлетворяют условиям D R (
, g, y) удовлетворяют условиям D R ( , g) = 0;
, g) = 0; 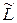 (
( , g, y) = 0 для
, g, y) = 0 для  = =g. Функция
= =g. Функция 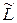 (
( , g, y) удовлетворяет требованиям, предъявляемым к функции потерь, поэтому рассмотрим квадратичную функцию потерь оценивания параметра g, при которой
, g, y) удовлетворяет требованиям, предъявляемым к функции потерь, поэтому рассмотрим квадратичную функцию потерь оценивания параметра g, при которой
|
|
|
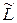 (
( , g, y) =
, g, y) =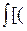
 0(y,
0(y,  ) – x)2 – (
) – x)2 – ( 0(y, g) – x)2] p (x | y, g) dx =
0(y, g) – x)2] p (x | y, g) dx =
=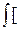
 0(y,
0(y,  ) – u 0(y, g)][
) – u 0(y, g)][ 0(y,
0(y,  ) +
) +  0(y, g)] p (x | y, g) dx –
0(y, g)] p (x | y, g) dx –
– 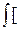
 0(y,
0(y,  ) –
) –  0(y, g)]2 xp (x | y, g) dx =
0(y, g)]2 xp (x | y, g) dx =
=[ 02(y,
02(y,  ) –
) –  02(y, g)]–2[
02(y, g)]–2[ 0(y,
0(y,  ) –
) –  0(y, g)]
0(y, g)] 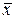 =
=
= [ 0(y,
0(y,  ) –
) – 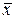 ]2– [
]2– [ 0(y, g) –
0(y, g) – 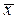 ]2,
]2,
а
D R ( , g) =
, g) =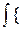 [
[ 0(y,
0(y,  ) –
) – 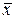 ]2 – [
]2 – [ 0(y, g) –
0(y, g) – 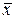 ]2} P (y |g) dy.
]2} P (y |g) dy.
Из данного выражения следует, что функция потерь
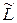 (
( , g, y)= [
, g, y)= [ 0(y,
0(y,  ) –
) –  0(y, g)]2– 2[
0(y, g)]2– 2[ 0(y,
0(y,  ) –
) –  0(y, g)][
0(y, g)][ 0(y, g) –
0(y, g) – 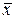 ]=
]=
= [ 0(y,
0(y,  ) –
) –  0(y, g)]2[1 – 2
0(y, g)]2[1 – 2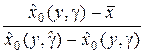 ]. (3.4)
]. (3.4)
Анализ уравнения (3.4) показывает, что функция потерь и, соответствующий ей, средний риск можно уменьшить не только за счет первого множителя, который характеризует уменьшение потерь на данном шаге оценки измеряемого параметра, но и второго сомножителя, анализ которого будет проведен в разд. 3.4.
Используя выражение для риска с функцией потерь (3.4) и учтя результаты из работы [83], получаем рекуррентное выражение для оценки математического ожидания 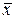 по экспериментальным данным:
по экспериментальным данным:
 n (y,
n (y,  ) =
) =  n –1(y,
n –1(y,  ) +
) +  Rn 1/2(
Rn 1/2( 0 n (y,
0 n (y,  ),
), 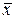 n). (3.5)
n). (3.5)
Величина R ( 0(y,
0(y,  ),
), 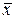 ) является функционалом оценки
) является функционалом оценки  = =
= = (y), который может принимать различные значения при разных значениях g. Поскольку истинное значение g неизвестно, то ни величина апостериорного риска, ни правило решения
(y), который может принимать различные значения при разных значениях g. Поскольку истинное значение g неизвестно, то ни величина апостериорного риска, ни правило решения  (y, g) не определены, и необходимо ввести новую меру ожидаемых потерь – оценку апостериорного риска, не зависящую от значения g. Оценкой величины R (
(y, g) не определены, и необходимо ввести новую меру ожидаемых потерь – оценку апостериорного риска, не зависящую от значения g. Оценкой величины R ( , y, g), обеспечивающей полное сохранение последующего байесова формализма, является
, y, g), обеспечивающей полное сохранение последующего байесова формализма, является
|
|
|
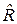 (
( , y) = R (
, y) = R ( , y,
, y,  ),
),
где  =
=  (y) – некоторая оценка значения g, найденная по данным наблюдения y. При подстановке
(y) – некоторая оценка значения g, найденная по данным наблюдения y. При подстановке 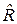 (
( , y) вместо неизвестного значения R (
, y) вместо неизвестного значения R ( , y, g) в правило решения (3.1), обеспечивающее минимум ожидаемых потерь при каждом значении y, получим правило решения
, y, g) в правило решения (3.1), обеспечивающее минимум ожидаемых потерь при каждом значении y, получим правило решения  (y)=
(y)= (y,
(y,  )=
)= (y,
(y,  (y)), отличающееся от оптимального байесова правила только заменой g оценочным значением
(y)), отличающееся от оптимального байесова правила только заменой g оценочным значением  =
= (y). Данная оценка
(y). Данная оценка  (y) должна обеспечить равномерно наилучшее приближение среднего риска правила решения
(y) должна обеспечить равномерно наилучшее приближение среднего риска правила решения  (y)=
(y)=  0(y,
0(y,  ) к минимальному байесову риску правила решения
) к минимальному байесову риску правила решения  0(y, g) с известным значением g. При равномерно наилучшем приближении максимальное отклонение должно быть минимальным, поэтому наилучшую оценку
0(y, g) с известным значением g. При равномерно наилучшем приближении максимальное отклонение должно быть минимальным, поэтому наилучшую оценку  (y)= =
(y)= = 0(y) следует выбирать, исходя из условия
0(y) следует выбирать, исходя из условия
 D R (
D R ( , g).
, g).
Таким образом, с учетом выражения (3.2) наилучшая оценка  0(y) является минимаксной оценкой параметра g плотности распределения вероятности P (y |g)=
0(y) является минимаксной оценкой параметра g плотности распределения вероятности P (y |g)=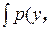 x |g) dx относительно функции потерь
x |g) dx относительно функции потерь 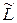 (
( , g, y) из (3. 3). Если множество значений параметров x непрерывно, то минимаксная оценка является оценкой максимального правдоподобия, то есть наилучшая оценка
, g, y) из (3. 3). Если множество значений параметров x непрерывно, то минимаксная оценка является оценкой максимального правдоподобия, то есть наилучшая оценка  0(y) совпадает с оценкой максимального правдоподобия
0(y) совпадает с оценкой максимального правдоподобия  0(y) = g*(y), которая определяется из уравнения правдоподобия P (y |g*) =
0(y) = g*(y), которая определяется из уравнения правдоподобия P (y |g*) = 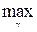 P (y |g) или, при отсутствии ограничений на область Г = { A l, B } значений g, – из эквивалентного ему уравнения
P (y |g) или, при отсутствии ограничений на область Г = { A l, B } значений g, – из эквивалентного ему уравнения
Ñgln P (y |g) = 0,
где Ñg = {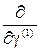 ,
,  ,...} – оператор градиента, ставящий в соответствие любой функции от g вектор - столбец частных производных этой функции по всем компонентам вектора g. Синтезированный алгоритм (3.5) оценки измеряемого параметра должен обеспечивать от шага к шагу сходимость его решения к
,...} – оператор градиента, ставящий в соответствие любой функции от g вектор - столбец частных производных этой функции по всем компонентам вектора g. Синтезированный алгоритм (3.5) оценки измеряемого параметра должен обеспечивать от шага к шагу сходимость его решения к 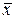 n и одновременную минимизацию второго слагаемого уравнения (3.4), то есть направленное движение к истинной оценке измеряемого параметра.
n и одновременную минимизацию второго слагаемого уравнения (3.4), то есть направленное движение к истинной оценке измеряемого параметра.
При использовании оценки максимального правдоподобия g*=g*(y), определяемой из уравнения правдоподобия P (y |g*) = 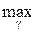 P (y |g), и адаптивном байесовом правиле оценивания
P (y |g), и адаптивном байесовом правиле оценивания  (y) =
(y) =  0(y, g*(y)) получается замкнутый конструктивный алгоритм, который заключается: в отыскивании оптимального байесова правила оценивания
0(y, g*(y)) получается замкнутый конструктивный алгоритм, который заключается: в отыскивании оптимального байесова правила оценивания  0(y, g) для фиксированного значения g путем минимизации апостериорного риска R (
0(y, g) для фиксированного значения g путем минимизации апостериорного риска R ( , y, g); нахождении оценки максимального правдоподобия g* = g*(y) путем решения уравнения правдоподобия; замене в оптимальном байесовом правиле оценивания
, y, g); нахождении оценки максимального правдоподобия g* = g*(y) путем решения уравнения правдоподобия; замене в оптимальном байесовом правиле оценивания  0(y, g) неизвестного значения g на его оценку g* = g*(y). При слабых ограничениях на функцию потерь L(
0(y, g) неизвестного значения g на его оценку g* = g*(y). При слабых ограничениях на функцию потерь L( , g, y), для которых оценка максимального правдоподобия g* является минимаксной оценкой, эта процедура обеспечивает получение правила оценивания
, g, y), для которых оценка максимального правдоподобия g* является минимаксной оценкой, эта процедура обеспечивает получение правила оценивания  (y), которое дает равномерно наилучшее приближение к среднему риску абсолютно оптимального байесова правила оценивания с известным значением g.
(y), которое дает равномерно наилучшее приближение к среднему риску абсолютно оптимального байесова правила оценивания с известным значением g.
|
|
|
При определении адаптивных байесовых правил решения используются рекуррентные методы определения оптимальных оценок параметров, которые обеспечивают минимизацию риска, в виде
 N +1 =
N +1 =  N + SNsN, N = 0, 1,..., (3.6)
N + SNsN, N = 0, 1,..., (3.6)
где  0 Î X – начальное приближение; sN – направление движения; SN ³0 – длина шага. В качестве начального приближения оценки
0 Î X – начальное приближение; sN – направление движения; SN ³0 – длина шага. В качестве начального приближения оценки  0 выбирают величину оценки, которая обеспечивает минимальный априорный риск для искомой оценки [1, 98] в соответствии с главами 2 и 3. Данные методы оптимизации различаются способом выбора направления движения sN, для которого должно обеспечиваться условие релаксационности. Причем число SN с точностью до множителя
0 выбирают величину оценки, которая обеспечивает минимальный априорный риск для искомой оценки [1, 98] в соответствии с главами 2 и 3. Данные методы оптимизации различаются способом выбора направления движения sN, для которого должно обеспечиваться условие релаксационности. Причем число SN с точностью до множителя  определяет расстояние от точки
определяет расстояние от точки  N до
N до  N +1. Трудоемкость вычисления величины SN должна быть согласована с трудоемкостью вычисления sN и SN.
N +1. Трудоемкость вычисления величины SN должна быть согласована с трудоемкостью вычисления sN и SN.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 324; Нарушение авторских прав?; Мы поможем в написании вашей работы!