Оптимальный одношаговый алгоритм

Общий АОЭИ является сложным и не всегда его применение может быть оправдано. Исходя из соотношения (3.5), для расчета оцениваемого параметра можно сформулировать существенно простой алгоритм его оценивания. Пусть процесс описывается уравнением в дискретные моменты времени:

у (N) = _i (N) х_i (N), (3.7)

где у (N) – выходная переменная в N -м такте; х_i (N) – значение i -го входа в N -м такте; h_i (N) – неизвестные параметры исследуемого процесса; n – число входов.

Модель постановки эксперимента, в соответствии c главой 2, можно представить в следующем виде:

у *(N) = 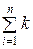_i (N – 1) х_i (N),

где у *(N) – оценка выхода объекта, полученная по модели; k_i (N –1) оценка i -го параметра исследуемого процесса для (N – 1)-го такта.

В соответствии с общим выражением для регуляризованного решения, полученного в §2.3, при вычислении x_i (N) на этапе редукции может быть использована следующая итерационная формула:

x_i (N)= x_i (N –1)+[ y (N)–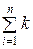 _i (N) x_i (N –1)] k_i (N)/[g+ 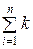_i ²(N)], (i = 1, 2,..., n). (3.8)

Переменные, входящие в эту формулу, можно оценить на этапе идентификации, а результатами, полученными по этой формуле, можно пользоваться при идентификации импульсной переходной функции первичного преобразователя. В выражении (3.8), выбрав совершенно произвольно начальные оценки x_i (0), можно на каждом такте производить их уточнение. Величина, на которую исправляются коэффициенты модели, пропорциональна ошибке предсказания:

D у (N) = у (N) – у *(N).

Алгоритм уточнения можно переписать в виде

x_i (N) = x_i (N – 1) + D y (N) k_i (N)/[g +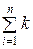 _i ²(N)] (i = 1, 2,..., n)

или еще проще

x_i (N) = x_i (N – 1) + D(N) k_i (N) (i = 1, 2,..., n),

где D(N) – величина, общая для всех входов и вычисляемая однажды в каждом такте, а длина шага S_N = D(N) k_i (N).

В векторной форме формула (3.8) будет иметь вид

x (N) = x (N – 1) + [ y (N) – k ^T(N) x (N – 1)] k (N)/[g + k ^T(N) k (N)] (3.9)

или

x (N)= x (N –1)+ [ h ^Т(N) x (N –1)– k ^T(N) x (N –1)] k (N)/[g+ k ^T(N) k (N)], (3.10)

где h ^T(N) – вектор истинных значений импульсной переходной функции датчика в N - м такте; k (N) – вектор оценок значений импульсной переходной функции датчика в N -м такте; x (N) – вектор входной переменной в N -м такте; у (N) – выходная переменная в N -м такте (скаляр); <т> – символ транспонирования.

Данные выражения можно написать еще проще:

x (N) = x (N – 1) + D(N) k (N), (3.11)

где скалярная переменная D(N) = , а q _x (N) = x – x (N) – вектор ошибки с составляющими,

q _x ^T(N) =,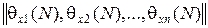

причем

q _xi (N) = x_i – x_i (N).

Для режима обучения, при котором ошибки определения параметров еще много больше вариации параметров, без потери общности можно принимать параметры процесса постоянными, не зависящими от N, а скалярный параметр алгоритма g, равным нулю. Подробнее влияние g исследовано [3].

Если производить уточнение оценок по формуле (3.11), то выражение для D(N + 1) можно получить из выражения (3.11), заменив вектор k (N) на вектор k (N + 1):

D(N + 1) = .

Выражая D(N + 1) через D(N), учитывая (3.11), получаем

D(N + 1) = .

Положив, что вектор k (N) равен вектору k (N + 1), имеем

D(N + 1) = D(N) 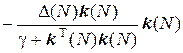= D(N). (3.12)

После s – кратного использования одних и тех же данных, производя такую операцию s раз и вычислив соответствующие оценки, получаем

x (N + s) = x (N – 1) + D(N) k (N).

При s ® ¥ формула упростится и примет вид

x (N + ¥) = x (N – 1) + 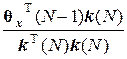k (N).

Используя повторные подстановки бесконечное число раз для любого g, получают тот же результат, что при оптимальном шаге, а при g≠0 выгодно производить уточнение оценок параметра объекта, даже если входные воздействия не изменяются.

С другой стороны, каждый коэффициент k_i (N – 1) уточняется пропорционально изменению переменной на его входе K_хxi (N). Аналогично, на этапе идентификации может быть использовано выражение

k_i (N)= k_i (N –1)+[ K_yx (N)–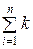 _i (N –1) K_xx (N)] K_xxi (N)/[g+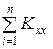² _i (N)],

(i =1, 2,..., n),

векторная форма которого имеет вид

k (N) = k (–1)+[ K _yx (N)– k ^T(N –1) K _xx (N)] K _xx (N)/[g + K _xx ^T(N) K _xx (N)] (3.13)

или

k (N)= k (N –1)+[ h ^Т(N) K _xx (N)– k ^T(N) K _xx (N)] K _xx (N)/[g+ K _xx ^T(N) K _xx (N)], (3.14)

где h ^T(N) – вектор истинных значений импульсной переходной функции датчика в N -м такте; k (N) – вектор оценок значений импульсной переходной функции датчика объекта в N -м такте; K _xx (N) – вектор корреляционных функций входной переменной в N -м такте; K_уx (N) – взаимная корреляционная функция входной и выходной переменной в N -м такте (скаляр); <т> – символ транспонирования.

Данное выражение можно привести к виду

k (N) = k (N – 1) + D(N) K _xx (N), (3.15)

где D(N) – скалярная переменная.

Проведенный анализ этапов редукции и идентификации привел к аналогичным типам алгоритмов, поэтому дальнейшее исследование алгоритмов можно осуществлять для одного типа алгоритма и распространить полученные результаты на другой тип. При этом следует отметить, что эти алгоритмы относятся к классу алгоритмов Язвинского в международной классификации [94].

Дата добавления: 2014-01-05