Общая постановка задачи формирования модели измерения

Формирование ММИ заключается в конструировании области определения модели, в которой достижимо простое разделение ее переменных, т. е. должна быть решена задача классификации. В качестве составляющих данной области выбираются некоторые параметры объектов (переменные модели), обладающие определенными особенностями относительно заданной модели. Все остальные параметры объектов в процессе формирования ММИ не учитываются, так как они несут информацию только об объекте, но не о модели, и не могут составить набор, гарантирующий простое разделение ее переменных. Переменные модели должны быть инвариантными – малочувствительными по отношению к встречающимся изменениям и искажениям и обладать небольшой избыточностью. При этом требуется осуществлять распознавание идентифицирующей ММИ путем решения задачи преобразования входной информации, в качестве которой рассматриваются признаки распознаваемой переменной формируемой модели, в выходную – в виде заключения о том, к какому классу модели относится распознаваемая переменная. Эта процедура представляет сложный итеративный процесс, однако достаточно несколько итераций для уточнения модели процесса оценивания.

Проведенный концептуальный анализ задачи формирования ММИ позволяет перейти к ее формальной постановке [3, 86]. Пусть в n – мерном евклидовом пространстве Rⁿ задана ограниченная замкнутая область определения модели D. Известно, что область D – объединение конечного числа допустимых классов (подобластей) К ₁,..., К_i, т.е.

D =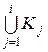

и задана некоторая начальная информация I ₀(К ₁,..., К_i) о классах, причем = Æ для всех i ¹ j, i, j = 1, 2,..., l. Задача формирования модели сводится к тому, что, используя лишь информацию I ₀(К ₁,..., К_i) для произвольного признака х Î D, заданного описанием I (х), требуется установить, к каким из классов К ₁,..., К_i принадлежит этот объект. При формировании начальной информации I ₀, если D – объединение непересекающихся подмножеств , i = 1, 2,..., t, т. е.

D = 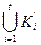, 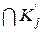= Æ, i ¹ j,

где 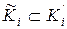– множества, определенные алгоритмами, то начальную информацию I ₀(К ₁,..., К_i) можно задавать континуальной обучающей информацией в виде набора <₁, ₁;...; _t, _t >, где _i – информационный вектор области _i, i = 1, 2,..., t.

Если классы К ₁,..., К_i – непересекающиеся (= Æ для всех i ¹ j, i, j = 1, 2,..., l), то = K_i, l = t. Если некоторые пересечения не пусты, то элементами каждого могут быть или объекты какого – либо класса, или объекты, одновременно принадлежащие двум или нескольким классам, т.е. некоторые элементы их пересечения. Поэтому отнесение алгоритмом объекта x в класс К_i означает, что x относится алгоритмом в соответствующие классы, пересечение которых есть . Если для каждого класса К ₁,..., К_i известны некоторые фиксированные подобласти _j Ì K_j, j = 1, 2,..., l (неважно, являются они замкнутыми или открытыми, достаточно лишь, чтобы мера m( _j) каждой из этих областей была не нулевая), то решение задачи формирования ММИ

Z = Z (I ₀(₁, ₁;...; _i, _i), X)

сводится к тому, чтобы для каждого 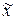Î X, используя лишь начальную информацию, представленную континуальной обучающей информацией

I ₀ = I ₀(₁, ₁;...; _i, _i),

где _i = ( _i) – информационный вектор области _i, i = 1, 2,..., l, определяется к какому из классов К ₁,..., К_i принадлежит данный признак. Качество решения данной задачи определяется степенью минимизации области

X Ì D \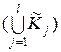

и, следовательно, для характеристики ее качества целесообразно оценивать риск решения задачи разбиения с функцией потерь вида

inf r(),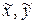

где 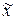Î X, .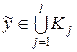

Алгоритм формирования ММИ:

A (x, I ₀) = (a₁(x, I ₀), a₂(x, I ₀),..., a _t (x, I ₀)), (4.1)

где a _i (x, I ₀): Rⁿ ´ J ®{0, 1} (i = 1, 2,..., t) – решающая функция, определенная для всех x Î Rⁿ; Rⁿ – признаковое пространство; I ₀Î J, J – множество стандартных начальных информаций о классах К ₁, К ₂,..., К_t Í Rⁿ, каждая стандартная начальная информация I Î J (таблица обучения) есть объединение конечных подмножеств данных классов.

Корректный метод и алгоритм формирования ММИ безошибочно классифицирует при любой стандартной начальной информации I ₀ все объекты x Î I ₀, то есть (a _i (x, I ₀)=1)«(x Î I ₀Ç K_i), i =1, 2,..., t. Осуществленное с помощью метода и алгоритма формирования общей ММИ (4.1) как разбиение на непересекающиеся подмножества , i = 1, 2,..., t позволяет рассчитать величину риска выбора модели каждой ее переменной (см. разд. 2.1), а также риск общей ММИ (см. следствие раздела 2.2). Причем, поскольку формирование ММИ задачи оценивания предполагает последовательное ее уточнение по мере накопления информации, то естественно его назвать асимптотическим методом формирования ММИ, для которой необходима разработка асимптотического метода формирования критерия качества задачи обобщенного оценивания, теоретическому обоснованию которого будет посвящены разделы 3.4 и 3.5.

Дата добавления: 2014-01-05