Типовые задачи и примеры их решения

Задача 6.1. Определить интервал дискретизации при оценке математического ожидания.

Решение задачи. Для решения данной задачи рассмотрим общие закономерности выбора оптимального в некотором смысле преобразователя для оценки математического ожидания исследуемого процесса. Как известно [32], дисперсия математического ожидания без квантования равна

D ₀(m 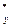) = (s/ N)[1+2, (6.1)

где D t – шаг выборки.

Если длительность реализации многократно превышает интервал корреляции, то (6.1) преобразовывается к виду

D ₀(m 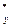) = (s/ N)[1+2, (6.2)

где t₀ = .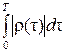

Будем считать, что длительность реализации Т постоянна. Тогда с некоторыми допущениями, обычно выполняющимися на практике, можно полагать, что нижний предел дисперсии D ₀(m 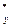) достигается при D t = 0 (непрерывное интегрирование) и равен [32]:

D _И0(m 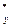) = (2s/ T)= (2s/ T). (6.3)

Для характеристики потерь точности, обусловленных дискретизацией, введем отношение дисперсий (6.2) к (6.3) при Т = const:

g= D ₀(m 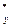) / D _И0(m 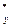) = D t /[1+2[2]. (6.4)

Соотношение (6.1) определяет шаг выборки при вычислении математического ожидания процесса таким образом, чтобы потери точности, обусловленные дискретизацией, были незначительными, т.е. в соответствии с комплексным критерием вида

.

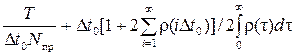Исследуем данный критерий на минимум, определяющий избыточность процесса дискретизации. Для этого продифференцируем его по D t ₀ и приравняем к нулю:

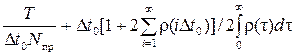{}_{D t}¢ = 0.

Из данного уравнения получаем дифференциальное уравнение первого рода

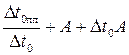– _{D t}¢ = 0,

которое в каноническом виде имеет вид

A _{D t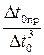}¢ + – = 0,

где А = .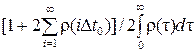

Решение данного дифференциального уравнения имеет вид [62]:

A = = ,

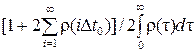где постоянная интегрирования равна

C = .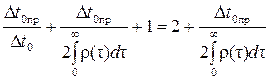

После подстановки полученной постоянной С получаем

=.

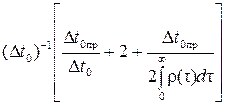Из анализа полученного решения видно, что оно определяется корреляционной постоянной и ее дискретным представлением 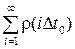. В связи с этим исследуем зависимость точности корреляционной функции r(t) от шага ее дискретизации.

Задача 6.2. Определить рациональный шаг выборки при вычислении корреляционной функции процесса.

Решение задачи. Оценка риска модели измерения, введенная в §1.2, определяется точностью оценки корреляционной функции процесса. Рассмотрим вопрос об оптимальном выборе шага выборки при вычислении корреляционной функции, одной из наиболее трудоемких для вычисления статистических характеристик. Воспользуемся для этого множительным алгоритмом вычисления корреляционной функции:

R ^*(j Dt) = 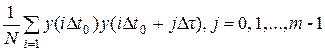. (6.5)

Будем полагать случайный процесс y (t) центрированным. Шаг задержки Dt устанавливается из условия хорошей аппроксимации R (t), что в общем случае сводится к хорошей аппроксимации случайного процесса y (t). При этом соседние отчеты, разделенные интервалом Dt, связаны значительными корреляционными связями. Однако шаг выборки Dt в алгоритме (6.5) необязательно устанавливать равным шагу задержки. Это нерационально ввиду большой избыточности вычислений. Для того чтобы показать это, исследуем погрешность вычисления корреляционной функции при t= 0. Полагая Т >>t₀, для дисперсии (6.5) в случае гауссовского случайного процесса будем иметь [43]:

D ₀[ R ^*(0)]».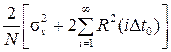

В случае некоррелированной выборки это соотношение примет вид

D ₀[ R ^*(0)]».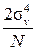

Избыточность вычислений по сравнению со случаем некоррелированной выборки можно характеризовать отношением объемов выборки N и N _нек, требуемых для достижения одинаковой статистической точности при выборке с шагом D t ₀ и D t > t_макс:

N/N _нек = 1+2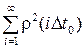. (6.6)

С некоторыми допущениями, как правило, выполняющимися на практике, можно принять, что максимальная точность на реализации фиксированной длительности достигается при D t ₀ = 0 (аналоговый случай) и дисперсия оценки R ^*(0) равна

D ₀[ R ^*(0)]=4.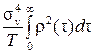

Ухудшение статистической точности, обусловленное дискретизацией, при Т = N D t ₀ = const составит

e² = D ₀[ R ^*(0)]/ D _0и[ R ^*(0)]=D t ₀[1+2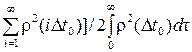. (6.7)

Критерий, обеспечивающий минимум относительной погрешности e² = = D ₀[ R *(0)]/ D _0и[ R* (0)] и минимум избыточности N / N _нек, с учетом выражений (6.6) и (6.7) имеет вид

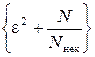_{D t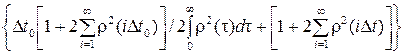}¢ = _{D t} ¢= 0.

Из полученного выражения получаем условие минимума:

B _{D t} ¢=0,

где В = .

Решение данного дифференциального уравнения первого порядка ищется методом разделения переменных [62]

– В _{D t} ¢/ В = d

и имеет вид

B ^-1= C,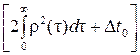

где постоянная интегрирования равна

C = .

После подстановки полученной постоянной решение исходного уравнения преобразуется к виду

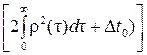/= B _пр/ B.

Для обеспечения условия D t ₀ = D t _0пр необходимо, чтобы B _пр /B =1, т.е. =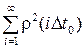. Умножив левую и правую части полученного уравнения на D t _0пр и используя представление интеграла суммой, получим

D t _0пр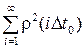==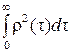t.

Из последнего выражения следует, что условие В/В _пр ®1 выполняется при D t ₀=D t _0пр ®(1 ¸ 0,5) t.

Из проведенного анализа следует, что интервал дискретизации должен быть близок к корреляционной постоянной оцениваемого процесса. Данному условию удовлетворяет и уравнение (6.2) для математического ожидания. Устанавливая шаг выборки равным D t ₀ ®(1 ¸ 0,5) t₀, можно добиться малой избыточности (максимум сжатия информации) при дискретизации, а потери точности, вызванные дискретизацией, будут незначительными. Для окончательных выводов по проведенному анализу, используя выражение (6.6) и представление интеграла в виде суммы, преобразуем выражение (6.7) к виду

e² = 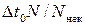[2D t ₀(N / N _нек – 1]= N /[2(N – N _нек)].

Из данного выражения следует, что при дискретизации условие e²» 1 сохраняется в случае уменьшения объема выборки до N _нек = N/ 2. При этом выражение (6.5), для полученного условия дискретизации D t ₀ = (1 ¸ 0,5), может быть преобразовано к виду

g=.

Таким образом, из (6.5) следует, что при варьировании объема выборки в достаточно больших пределах величина у изменяется в интервале (1,5 ¸ 1,25), а среднеквадратическое отклонение соответственно в диапазоне (1,2 ¸ 1,1). Поскольку при получении (6.5) пренебрегли одним из слагаемых малой величины, то диапазон изменения средне-квадратического отклонения оказывается еще меньше полученного. Случай выбора шага выборки D t в выражении (6.5) равным шагу задержки ( D t = Dt) соответствует значениям D t = (0,1 ¸ 0,3)t₀. При этом достигается практически такая же точность, что и при аналоговом методе. Однако избыточность вычислений по сравнению с некоррелированной выборкой значительна: N/N _нек= 3 ¸ 10.

Для некоррелированной выборки, когда D t > 3t₀, положение обратное: избыточность вычислений практически отсутствует, а потери, обусловленные дискретизацией, становятся существенными. При D t = t₀ достигается малая избыточность вычислений для исследуемого процесса с корреляционными функциями типа (6.5), в то же время потери точности, вызванные дискретизацией, оказываются незначительными.

Задача 6.3. Оценить риск квантования аналогового сигнала.

Решение задачи. В соответствии с общей оценкой риска, определим риск квантования аналогового сигнала как усредненную функцию потерь, к которой приводит решение о представлении (замене) исходной аналоговой величины ее квантованной формой. Для этого учтем, что, как показано в работе [109], плотность вероятности ошибки квантования имеет вид, близкий к равномерному закону распределения:

p_v (y) = Dt, ,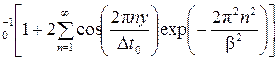

где у – выходной параметр измерительного преобразователя; v – ошибки, сопровождающие процесс измерения.

При этом оценка = 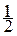(Y ⁺ + Y ^-) минимаксна, а ее риск равен

R ()=,

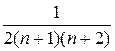где Y ⁺ = max (Y ₁, Y ₂, ..., Y_n), Y ^- = min (Y ₁, Y ₂, ..., Y_n).

Причем плотность распределения полного эксперимента, состоящего из п независимых измерений с равномерной плотностью распределения f (Y_i) = (Y⁺) ^{- 1}, определяется в виде Р 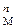= 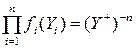Искомая статистика для оценки среднего значения результатов измерения должна характеризоваться минимальным риском при минимальном количестве измерений, т.е. оценка должна быть байесовской, которая для равномерного закона распределения совпадает с питменовской [2]:

= =,

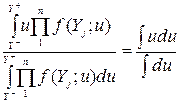где ⁺ = max (₁, ₂, ..., _n), ^- = min (₁, ₂, ..., _n). Дисперсия данной оценки математического ожидания равна

D = .

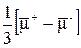Полученная оценка математического ожидания минимаксна. Учтя, что математическое ожидание случайной величины, умноженной на постоянный коэффициент, равно математическому ожиданию случайной величины, умноженному на заданный постоянный коэффициент [62], выражение для риска оценки математического ожидания M для равномерного закона распределения из работы [1] преобразуется к виду

R = E_M .

Дата добавления: 2014-01-05