Описание тренда с помощью методов сглаживания

3.1. Механическое выравнивание (сглаживание)

Механическое выравнивание (или сглаживание) отдельных частей ряда динамики выполняется с использованием фактических значений соседних уровней.

Существуют различные методы механического выравнивания.

Метод усреднения по левой и правой половине:

1. Разделяют ряд динамики на две части.

2. Находят для каждой из них среднее арифметическое значение.

3. Проводят через полученные точки линию тренда на графике.

Метод укрупнения интервалов. В том случае, если рассматриваются уровни экономических показателей за короткие промежутки времени, то в силу влияния различных факторов, действующих в разных направлениях, в рядах динамики наблюдается снижение и повышение этих уровней. Это мешает видеть основную тенденцию развития изучаемого явления. Поэтому для наглядного представления тренда применяется метод укрупнения интервалов, основанный на укрупнении периодов времени, к которым относятся уровни ряда (например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т.д.).

Метод простой скользящей средней. Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней начиная со второго, далее – начиная с третьего и т.д. Т.о., при расчетах среднего уровня как бы «скользят» по ряду динамики от начало до конца, каждый раз отбрасывая один уровень в начале и добавляя один следующий. Отсюда название – скользящая средняя. Каждое звено скользящей средней – это средний уровень за соответствующий период, который относится к середине выбранного периода.

Метод взвешенной скользящей средней Взвешенная скользящая средняя отличается от простой скользящей средней тем, что уровни, входящие в интервал усреднения, суммируются с различными весами. Это связано с тем, что аппроксимация ряда динамики в пределах сглаживания осуществляется с использованием уровней, рассчитанных по полиному … (здесь i – порядковый номер уровня в интервале сглаживания). Полином 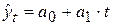есть уравнение прямой, следовательно, метод простой скользящей средней является частным случаем метода взвешенной скользящей средней. Коэффициенты полиномов находят по методу наименьших квадратов. При данном методе сглаживания сначала определяется интервал сглаживания и порядок параболы (аппроксимирующего полинома). Считается, что при использовании полиномов высоких степеней и при меньших размерах интервалов сглаживание ряда динамики будет более «гибким». Поскольку i = …, -2, -1, 0, 1, 2, …, то сглаженное значение уровня рано параметру 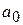подобранной параболы и является соответствующей скользящей средней.

3.2. Выравнивание с применением кривой.

На практике для описания тенденции развития явления широко используются модели кривых роста, представляющие собой различные функции времени y = f (t). При таком подходе изменение исследуемого показателя связывают лишь с течением времени. Правильно выбранная модель кривой роста должна соответствовать характеру изменения тенденции исследуемого явления. Кривая роста позволяет получить выровненные или теоретические значения уровней динамического ряда. Это те уровни, которые наблюдались бы в случае совпадения динамики явлений с кривой. Прогнозирование на основе модели кривой роста базируется на экстраполяции, т.е. на продление в будущее тенденции, наблюдавшейся в прошлом, при этом сложившаяся тенденция не должна претерпевать существенных изменений в течение периода упреждения.

Тенденция динамики связана с действием долговременно существующих причин и условий развития.

Колебания связаны с действием краткосрочных (циклических) факторов, влияющих на отдельные уровни динамического ряда и отклоняющих уровни от тенденции то в одном, то в другом направлении.

При статистическом изучении динамики необходимо четко различить два ее элемента – тенденцию и колеблемость (их смешение ведет к неверным выводам), чтобы дать каждому из них количественную характеристику с помощью специальных показателей.

Для того чтобы построить систему показателей, характеризующих тенденцию динамики, необходимо выяснить:

– какие черты, свойства этой тенденции необходимо измерить и выразить в статистических показателях (как в абсолютном, так и в относительном выражении);

– является ли изменение равномерным или неравномерным; ускоренным или замедленным;

– как выразить тенденцию в форме некоторого достаточно простого уравнения, наилучшим образом аппроксимирующего фактическую тенденцию динамики.

Уравнение тенденции динамики называется трендом(?).

Прежде чем применить методы математического анализа для вычисления параметров уравнения тренда, необходимо выявить тип тенденции, а это задача не является чисто математической. Наличие колебаний уровней крайне усложняет выявления типа тенденции. При качественном изучении характера развития объекта нужно выяснить:

– были ли условия для развития объекта достаточно однородными в изучаемом периоде

– каков характер основных факторов развития;

– не произошло ли качественное, существенное изменение условий развития объекта внутри изучаемого периода времени.

Например, часть периода предприятие работало по старой технологии, а затем произошло техническое перевооружение (введены новые поточные линии, цехи), то единой тенденции показателей за весь период не будет, т.е. нужно дробление его на отдельные периоды.

3.2.1. Выявление типа тенденции динамики.

Основные типы уравнения тренда

В литературе описано большое число типов уравнений тренда, которые можно условно разделить на три класса в зависимости от того, какой тип динамики развития они лучше описывают.

К I классу относятся функции, используемые для описания процессов с монотонным характером развития и отсутствием пределов роста (характерно, например, для показателей промышленного производства в натуральном выражении).

Ко II классу относятся кривые, описывающие процесс, который имеет предел роста в исследуемом периоде (примеры: демография, потребности в товарах и услугах в расчете на душу населения, предположим, среднедушевое потребление определенных продуктов питания, эффективность использования ресурсов, расход удобрения на единицу площади и т.п.).

К III классу относятся кривые насыщения, имеющие точки перегиба, а именно S- образные кривые. Эти кривые описывают как бы два последовательных лавинообразных процесса (когда прирост зависит от уже достигнутого уровня): – один с ускорением развития, другой – с замедлением, т.е. характерны для развития, проходящего все фазы (например, процесс насыщения потребителей каким либо новым товаром, скажем, телевизорами: сначала медленный, но все ускоряющийся рост доли семей, имеющих телевизор, затем рост равномерный – от 30% семей до 80% – затем рост доли семей, имеющих телевизор, замедляется по мере приближения доли к 100%; демографические исследования; страховые расчеты; задачи прогнозирования научно-технического прогресса и т.п.).

Вопрос о выборе кривой является основным при выравнивании ряда.

Остановимся на некоторых практических подходах, облегчающих процесс выбора кривой роста:

а) визуальный (наиболее простой путь), опирающийся на графическое изображение временного ряда – подбирают такую кривую роста, форма которой соответствует фактическому развитию процесса;

б) если на графике исходного ряда тенденция недостаточно четко просматривается, то проводят некоторые стандартные преобразование ряда (например, сглаживание), а потом подбирают функцию, отвечающую графику преобразованного ряда;

в) при выборе кривых типа , т.е. в виде полиномов, применяется метод последовательных разностей, заключающийся в вычислении первых, вторых и т.д. разностей вида: , ; и расчет ведется до такого порядка, пока разности не станут примерно равными, и этот порядок разностей принимается за степень выравнивающего полинома;

г) чаще всего на практике к выбору формы кривой подходят, исходя из значения критерия, в качестве которого принимают сумму квадратов отклонений фактических значений уровней от расчетных, полученных выравниванием, при этом предпочтение будет отдано той кривой, которой соответствует минимальное значение критерия, ибо чем меньше значение критерия, тем ближе к кривой ложатся данные наблюдений.

1. Линейная форма тренда (относится к I классу):

,

где – уровни, освобожденные от колебаний, выровненные по прямой;

a – начальный уровень тренда в момент (или период), принятый за начало отчета времени t;

b – среднегодовой абсолютный прирост (среднее изменение за единицу времени); константа тренда.

Хорошо отражает тенденцию изменений при действии множества разнообразных факторов, изменяющимся различным образом по разным закономерностям, которые взаимопогашаются (например, тенденция динамики урожайности для масштаба области, страны в целом).

2. Параболическая форма тренда (относится к I классу):

,

где с – квадратический параметр (константа), равный половине ускорения; остальные обозначения прежние.

Выражает ускоренное (замедленное) изменение уровней ряда с постоянным ускорением (например, при прогрессирующем поступлении высокопроизводительного оборудования; ускоренное возрастание может происходить в период после снятия каких-то сдерживающих развитие преград – ограничений в распределении дохода, в уровне оплаты труда; при повышении цены на дефицитную продукцию). Заметим, отрицательное ускорение (c < 0) приводит со временем не только к приостановке роста уровня, но и к его снижению со все большей скоростью (например, при производстве устаревшей продукции). Парабола 2-го порядка имеет либо минимум, либо максимум.

3. Экспоненциальная форма тренда (относится к I классу):

,

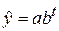где b – постоянный темп роста в разах (темп роста равен );

a – константа тренда.

k > 1 – тренд выражает тенденцию ускоренного и все более ускоряющегося («лавинообразного» – прирост зависит от достигнутого уровня) возрастания уровней (например, размножение организмов при отсутствии ограничения со стороны среды: сорняки, хищники, вирусные заболевания); рост любого объекта по экспоненциальному закону может продолжаться только небольшой исторический период. k < 1 – тенденция постоянного все более замедляющегося снижения уровней динамического ряда (например, динамика удельных затрат при технологическом прогрессе). Экстремальных точек не имеет.

4. Логарифмическая форма тренда (относится к I классу):

.

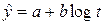Пригоден для отображения тенденции замедляющегося роста уровней при отсутствии предельно возможного значения (например, для отображения роста спортивных достижений); замедление роста становится все меньше и меньше, и при достаточно большом t становится малоотличимой от прямой линии; экстремума не имеет.

5. Тренд в форме степенной кривой (относится к I классу):

,

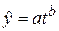где b – константа тренда.

Гибкая, пригодная для отображения изменений с разной мерой пропорциональности изменений во времени: при b =1 – линейный тренд, при b =2 – параболический и т.п. При k = 0 = 0. Общая форма 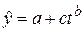ввиду невозможности логарифмировать применяется крайне редко.

6. Модифицированная экспонента (относится ко II классу):

,

где y = k – горизонтальная асимптота.

Для процессов, характеризующихся «насыщением»: если a < 0 – асимптота находится выше кривой, если a > 0, – то ниже (в экономической практике чаще всего находит применение случай, когда a < 0, b < 1, в этом случае рост уровней происходит с замедлением и стремится к некоторому пределу). Хорошо описывает процесс, на развитие которого воздействует ограничивающий фактор (например, главный инженер предприятия указывает, что производственные мощности не позволяют наращивать объемы производства выше определенного уровня k) – в этом случае уравнение можно линеаризовать.

7. Гиперболическая форма тренда (относится ко II классу):

.

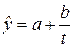Подходит для отображения тенденции, процессов, ограниченных предельным значением уровня (например, предельный коэффициент полезного действия двигателя, предел 100%-ной грамотности населения), т.к. при b > 0 (b < 0) тренд соответствует тенденции замедляющегося снижения (роста) уровня, стремящегося к пределу a.

8. Кривая Гомперца:

,

где y = k – горизонтальная асимптота.

Для решения экономических задач наибольший интерес представляет вариант кривой, когда log a < 0 и b < 1 (в этом случае относится к III классу, при log a > 0 и b > 1 относится ко II классу). Кривая асимметрична и развитие уровня кривой имеет следующие этапы: на первом этапе прирост кривой незначителен (он медленно увеличивается по мере роста t), но на следующем этапе прирост увеличивается быстрее, а затем, после точки перегиба, начинает уменьшаться, и на подходе к линии асимптоты прирост кривой опять незначителен.

9. Логистическая форма тренда (кривая Перла-Рида) (относится к III классу):

,

где и – максимальное и минимальное из возможных значений уровня;

a, b – параметры тренда;

Если = 0 и = 0, уравнение принимает следующий вид:

.

Кривая симметрична относительно точки перегиба с координатами: t = ln b: a; .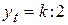

С помощью этой функции хорошо описывается развитие новой отрасли (нового производства). Сначала технические методы производства еще недостаточно разработаны, издержки производства высоки и спрос на рынке на данный товар еще очень мал, поэтому производство развивается медленно. В дальнейшем, благодаря усовершенствованию технических методов изготовления, переходу к массовому производству и увеличению емкости рынка для данного товара производство растет быстрее. Затем наступает период насыщения рынка, рост производства все более замедляется, и наконец почти прекращается. Наступает стабилизация на определенном уровне (однако выявленные закономерности развития следует обобщать с определенной осторожностью, причем для коротких периодов, например, выявленная тенденция развития производства может быть нарушена вследствие технического перевооружения в данной отрасли или в связи с ним).

Замечания к теме «Выявление типа тенденции динамики»:

1. Оценки параметров в вышеназванных моделях находятся методом наименьших квадратов (МНК). Как известно, суть его состоит в определении таких коэффициентов (параметров), при которых сумма квадратов отклонений расчетных значений уровней от фактических была бы минимальной, т.е. (n – длина временного ряда), поэтому выбранные уравнения необходимо привести к линейному, относительно искомых параметров, виду.

2. Обычно в экономических исследованиях применяются полиномы не выше третьего порядка. Использовать для определения тренда полиномы высоких степеней нецелесообразно, поскольку полученные таким образом аппроксимирующие функции будут отражать случайные отклонения (что противоречит смыслу тенденции).

3. К ряду, состоящему из m точек, можно подобрать многочлен (полином) степени (m – 1), проходящий через все m точек, но очевидно, что такая кривая не слишком пригодна как для выделения тенденции, так и для целей прогнозирования.

4. При выборе типа модели необходим содержательный анализ изучаемого процесса. Например. Предположим, на ретроспективном участке ряд динамики может быть хорошо описан с помощью экспоненциальной кривой. Однако первая половина логистической кривой также представлена экспонентой. Поэтому принять гипотезу об экспоненциальной тенденции ряда в будущем можно только после проведения содержательного анализа, в ходе которого следует дать ответ на вопрос: возможно ли наступление «насыщения» при данной совокупности условий.

5. Не исключена ситуация, когда наилучшей функцией по данному критерию будет признана прямая, но тогда возможно получение отрицательного прогнозного значения, которое из экономических соображений не может быть отрицательным (например, прогнозирование объема выпускаемой продукции). В этом случае следует отказаться от этой функции, выбрав менее «удачную», но соответствующую содержательному смыслу показателя (например, более подходящей в этом случае может оказаться экспоненциальная кривая при значении параметра b < 1).

6. Отметим, что не существует «жестких» рекомендаций для выбора кривых роста. Особенно осторожно следует подходить к решению этой задачи при использовании полученной функции для экстраполяции найденных закономерностей в будущее. Применение кривых должно базироваться на предположении о сохранении выявленной тенденции в прогнозируемом периоде.

Рассмотренные в данном разделе различные статистические приемы и методы могут помочь исследователю при осуществлении сложного выбора подходящей кривой роста.

Дата добавления: 2014-01-05