Задачи линейного программирования

ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ ОПРЕДЕЛЕННОСТИ

Инструментом моделирования распределения ресурсов для достижения цели чаще всего являются методы линейного программирования.

Задача линейного программирования является частным случаем задачи оптимизации и записывается в следующем виде:

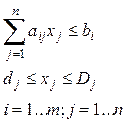
Задачу линейного программирования можно решать графическими и аналитическими методами. Одним из самых известных аналитических методов по праву считается симплекс-метод, который реализован в Excel (симплексом тела в k-мерном пространстве называют совокупность k+1 его вершин). Алгоритм симплекс-метода обеспечивает переход от одной вершины к другой в таком направлении, при котором значение целевой функции от вершины к вершине улучшается. Поэтому и аналитический метод, основанный на итерациях вычисления целевой функции и переменных в вершинах, с учетом этого получил свое название.

Рассмотрим сам метод, его реализацию в Excel и, самое главное, анализ результатов с целью принятия решений на примере, приведенном в книге[3] задачи распределения ресурсов.

Задача. Требуется определить, в каком количестве надо выпускать продукцию типов Прод1, Прод2, Прод3, Прод4 с целью получения наибольшей прибыли. Известно, что для изготовления требуются ресурсы трех видов: трудовые, сырье, финансы. Количество каждого ресурса на момент решения задачи, норма расхода каждого вида ресурса на единицу продукции каждого типа и прибыль от реализации единицы продукции известны и приведены в таблице на рис. 1.

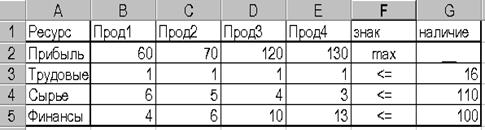Рис.1

Введем обозначения:

x_j – количество выпускаемой продукции j-го типа (j= 1…4);

b_i – количество наличного ресурса i-го вида (i= 1…3);

a_ij – норма расхода i-го ресурса для выпуска единицы продукции j-го типа;

c_j – прибыль, получаемая от реализации единицы продукции j-го типа.

Математическая модель задачи имеет вид:

F == 60x₁ +70x₂ + 120x₃ +130x₄ Þ max

x₁ + x₂ + x₃ + x₄ <= 16

6x₁ +5x₂ +4x₃ + 3x₄ <= 110

4x₁ + 6x₂ +10x₃ + 13x₄ <= 100

x_ij >=0, j = 1…4

Вычисление всех искомых значений обеспечивает Excel с помощью надстройки Сервис–Поиск решения.

Дата добавления: 2014-01-05